
🔥小叶-duck :个人主页
❄️个人专栏:《Data-Structure-Learning》
《C++入门到进阶&自我学习过程记录》《算法题讲解指南》--从优选到贪心
✨未择之路,不须回头
已择之路,纵是荆棘遍野,亦作花海遨游
目录
03.快乐数
题目链接:
题目描述:

题目示例:

题目分析:
为了方便叙述,将【对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和】这一个操作记为 x 操作;
题目已经告诉我们,当我们不断重复 x 操作的时候,计算一定会【循环】,循环方式有两种:
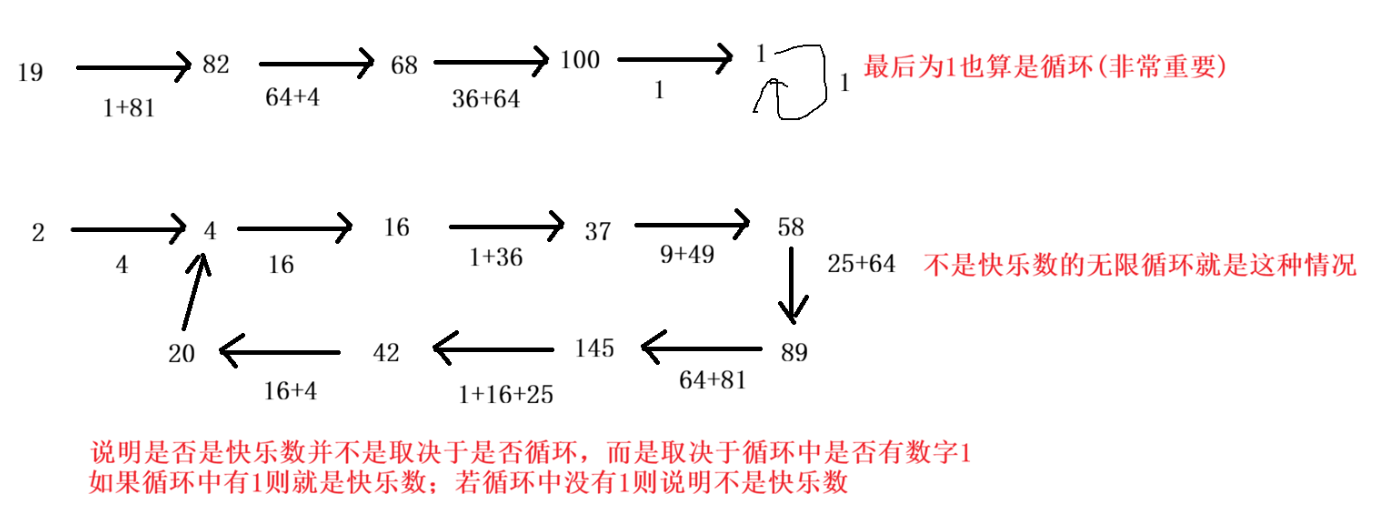
- 情况一: 一直在 1 中进行循环,即 1 -> 1 -> 1- > 1......
- 情况二: 在历史的数据中进行循环,但始终变不到 1
由于上述两种情况只会出现一种,因此,只要我们能够确定循环时在【情况一】中进行,还是在【情况二】中进行,就能得到结果。
简单证明(为什么一定循环):
- 经过依次变化之后的最大值9^2*10=810 (2^31-1=2147483647。 选一个更大的最大9999999999 ),也就是变化的区间在**【1,810】**之间;
- 根据【鸽巢原理】,一个数变化 811 次之后,必然会形成一个循环;
- 所以,变化的过程最终一定会走到一个圈里面,因此可以用【快慢指针】来解决。
解法:(快慢指针)
算法思路:
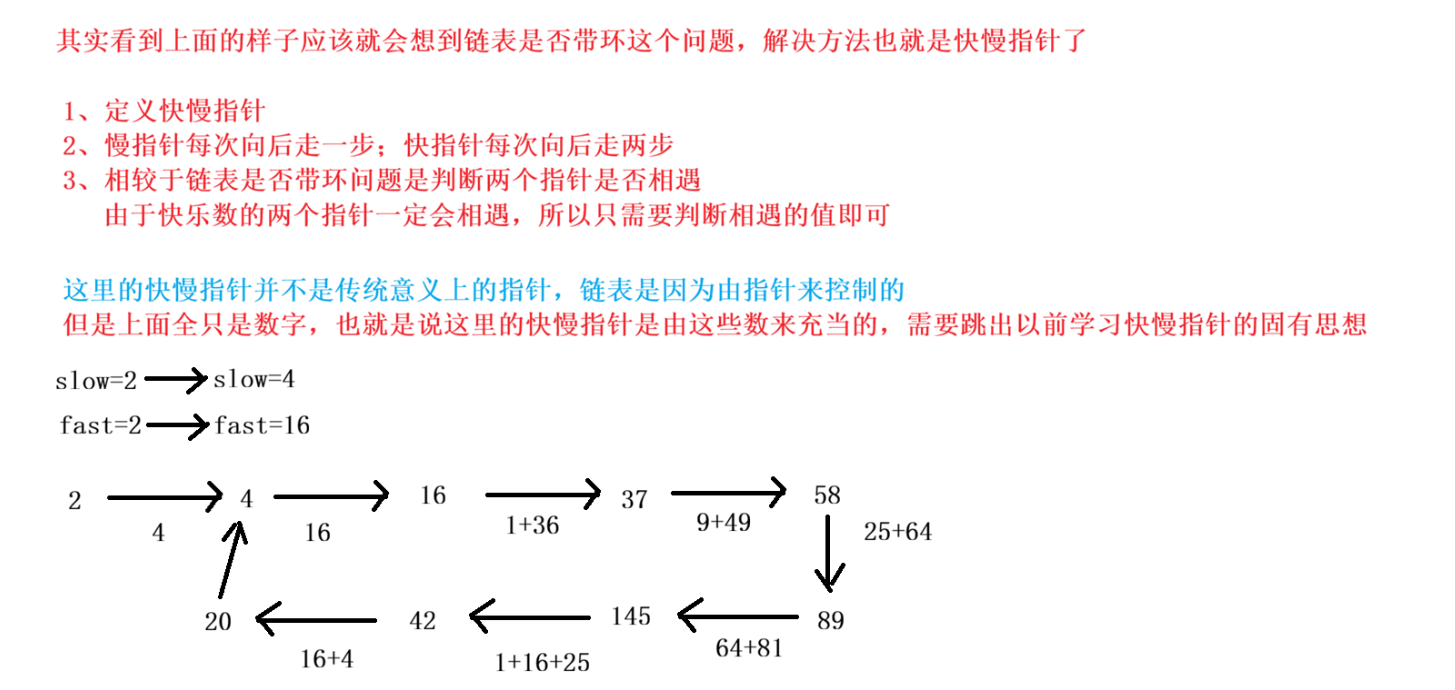
根据上述的题目分析,我们可以知道,当重复执行 x 的时候,数据会陷入到一个【循环】之中。而【快慢指针】有一个特性,就是在一个圆圈 里,快指针总是会追上慢指针 的,也就是说他们总会相遇在一个位置上。如果相遇的位置的值是 1 ,那么这个数一定是快乐数;如果相遇的位置不是 1 的话,那么就不是快乐数。
C++代码演示:
cpp
class Solution {
public:
int sum(int n)
{
int sum = 0;
int rem = 0;
while(n)
{
rem = n % 10;
n /= 10;
sum += (rem * rem);
}
return sum;
}
bool isHappy(int n)
{
int slow = n;
int fast = sum(n);
//初始化让fast到第二个数
//因为两者一定会重合,所以如果同时初始化n则while进不去
while(slow != fast)
{
slow = sum(slow);
// fast = sum(fast);
// fast = sum(fast);
fast = sum(sum(fast));
}
// if(slow == 1)
// {
// return true;
// }
// return false;
return slow == 1;
}
};算法总结及流程解析:

04.盛水最多的容器
题目链接:
题目描述:

题目示例:
算法思路:
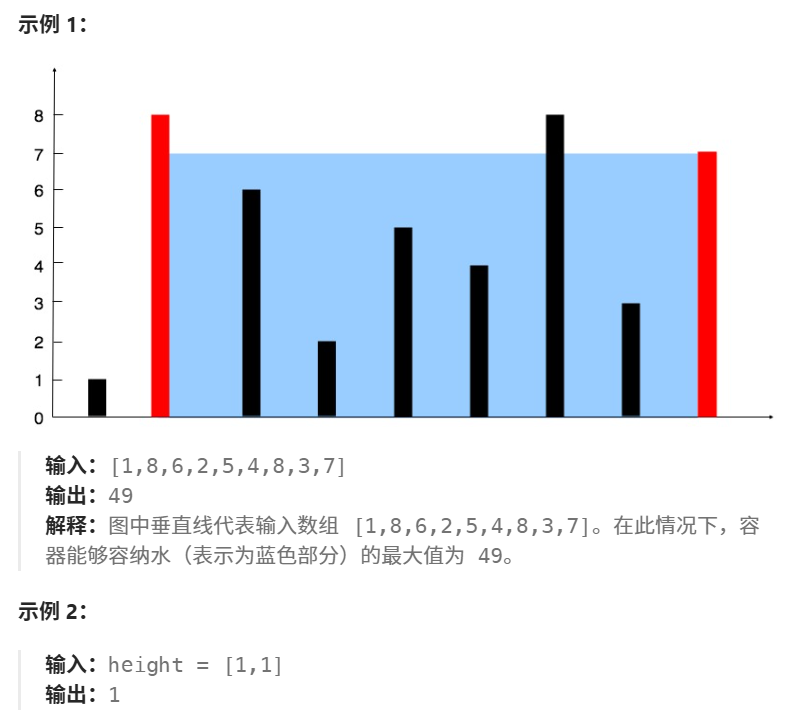
设两个指针left ,right分别指向容器的左右两个端点,此时容器的容积:
v = (right - left)* min( height[ right ],height[ left ] )
容器的左边界为 height[ left ] ,右边界为 height[ right ]。
为了方便叙述,我们假设 【左边边界】小于 【右边边界】。
如果此时我们固定一个边界,改变另一个边界,水的容积会有如下变化形式:
- 容器的宽度一定变小
- 由于左边界较小,决定了水的高度。如果改变左边界,新的水面高度不确定,但是一定不会超过右边的柱子高度,因此容器的容积可能会增大。
- 如果改变右边界,无论右边界移动到哪里,新的水面高度一定不会超过左边界,也就是不会超过现在的水面高度,但是由于容器的宽度减小,因此容器的容积是一定会变小的。
由此可见,左边界和其余边界的组合情况都可以舍去。所以我们可以 left++ 跳过这个边界,继续去判断下一个右边界。(在本题里就是先比较左右谁小,如果左边小就left++,右边小就right--)
当我们不断重复上述过程,每次都可以舍去大量不必要的枚举过程 ,直到left 与right 相遇。期间产生的所有的容积里面取最大值,就是最终答案。
C++代码演示:
cpp
class Solution {
public:
int maxArea(vector<int>& height)
{
int v_max = 0;
int v = 0;
int left = 0;
int right = height.size() - 1;
while(left < right)
{
int h_min = min(height[left], height[right]);
v = (right - left) * h_min;
if(h_min == height[left])
{
left++;
}
else
{
right--;
}
if(v > v_max)
{
v_max = v;
}
}
return v_max;
}
};算法总结及流程解析:


结束语
到此,03.快乐数和04.盛水最多的容器两道算法题就讲解完了。**快乐数问题采用快慢指针法判断循环类型,盛水容器问题利用对撞指针优化计算。**希望大家能有所收获!