LM 在 PnP（EPnP / P3P）的应用

1. PnP + LM 的优化目标函数

我们要优化 姿态 (R,t)，使重投影误差最小：

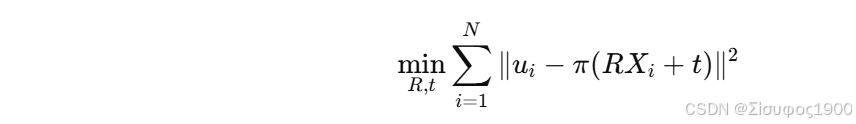
投影模型：

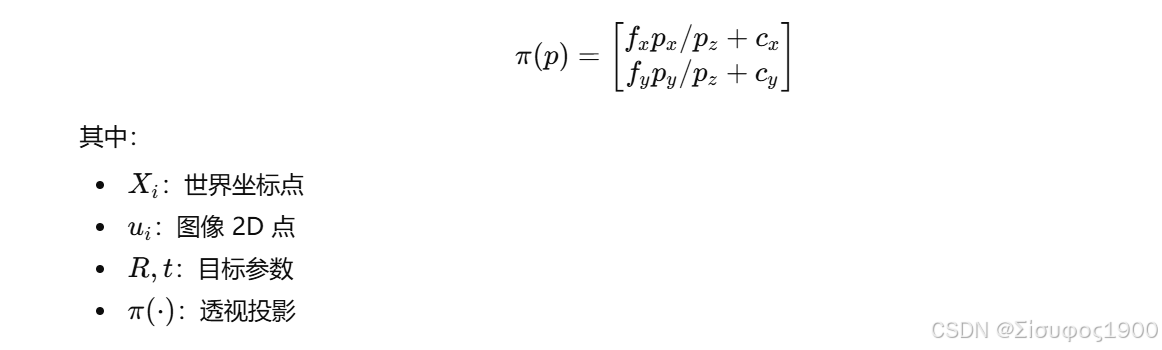
2. LM 在 PnP 中的迭代公式

LM 的通式：

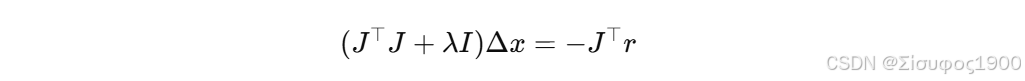PnP 的参数向量 用最小参数化的李代数 se(3)：

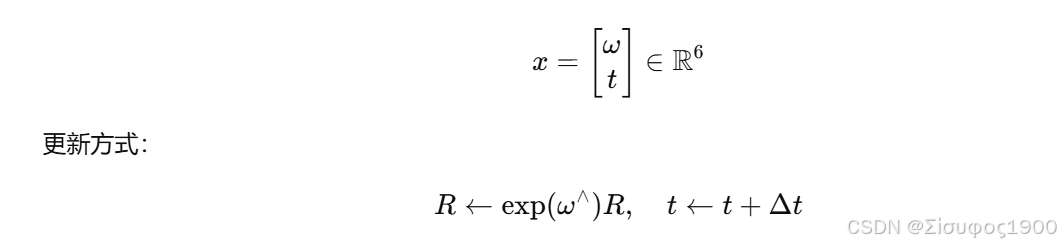
3. 重投影误差 Jacobian（核心推导）

对每个点：

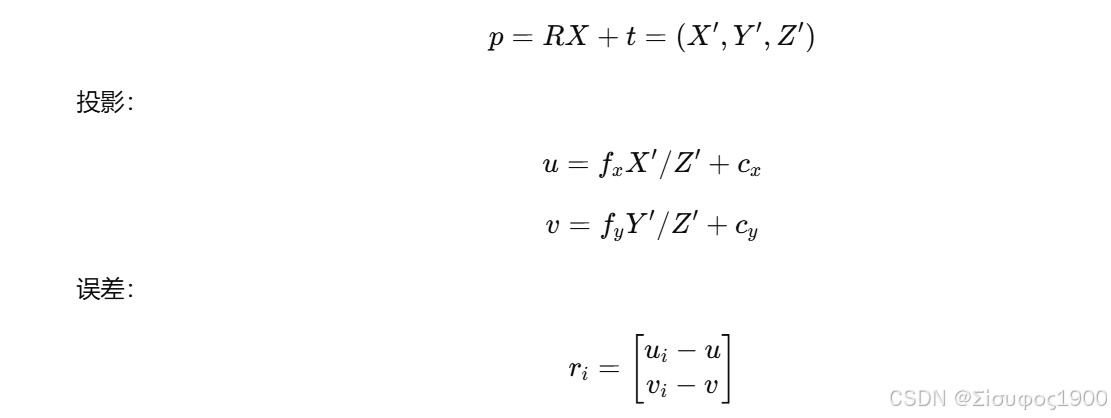
对p=RX+t 的导数：

位姿的雅可比（李代数）：

4. MATLAB ------ EPnP + LM

功能：

生成或读取匹配点
用 EPnP 求初值
使用 LM 优化相机位姿
输出 R,t
重投影误差下降明显

cs 复制代码

function [R, t] = pnp_LM(Xw, x2d, K)

% Xw: Nx3 3D points
% x2d: Nx2 image points
% K: intrinsic matrix

%% ---------- Step 1: EPnP 获取初始姿态 ----------
[R, t] = efficient_pnp(Xw, x2d, K);  
% 你可以换成自己的 EPnP；这里只是一个实现接口


%% ---------- Step 2: LM 优化 ----------
maxIter = 20;
lambda = 1e-3;

for iter = 1:maxIter

    r = [];     % residual vector
    J = [];     % full Jacobian

    for i = 1:size(Xw,1)
        Xi = Xw(i,:)';

        % ---- transform ----
        Pc = R * Xi + t;
        Xp = Pc(1); Yp = Pc(2); Zp = Pc(3);

        % ---- projection ----
        u = K(1,1)*Xp/Zp + K(1,3);
        v = K(2,2)*Yp/Zp + K(2,3);

        % ---- residual ----
        ri = [x2d(i,1) - u;
              x2d(i,2) - v];
        r = [r; ri];

        % ---- Jacobian wrt p = (X',Y',Z') ----
        du_dp = [K(1,1)/Zp, ...
                 0, ...
                -K(1,1)*Xp/Zp^2];
        dv_dp = [0, ...
                 K(2,2)/Zp, ...
                -K(2,2)*Yp/Zp^2];
        J_proj = [du_dp; dv_dp];  % 2x3

        % ---- Jacobian wrt pose (omega, t) ----
        px = Pc;
        px_hat = [ 0, -px(3), px(2);
                   px(3), 0, -px(1);
                  -px(2), px(1), 0 ];

        J_se3 = [ -px_hat, eye(3) ];   % 3x6

        Ji = J_proj * J_se3;  % 2x6
        J = [J; Ji];
    end

    % ---- LM step ----
    H = J' * J;
    g = J' * r;
    delta = -(H + lambda * eye(6)) \ g;

    % ---- Update pose using Lie algebra ----
    omega = delta(1:3);
    dt = delta(4:6);

    % SO(3) 更新
    R = expSO3(omega) * R;

    % 平移更新
    t = t + dt;

    % 减少 lambda（如果误差下降）
    new_r = compute_residual(Xw, x2d, R, t, K);
    if norm(new_r) < norm(r)
        lambda = lambda / 10;
    else
        lambda = lambda * 10;
    end

    fprintf("Iter %d, reprojection error = %.6f\n", iter, norm(new_r));
end

end


%% ======== 工具函数：SO(3) 指数映射 ========
function R = expSO3(w)
theta = norm(w);
if theta < 1e-12
    R = eye(3); return;
end
k = w / theta;
K = [0 -k(3) k(2);
     k(3) 0 -k(1);
     -k(2) k(1) 0];
R = eye(3) + sin(theta)*K + (1-cos(theta))*K*K;
end


%% ======== 工具函数：计算重投影误差 ========
function r = compute_residual(Xw, x2d, R, t, K)
r = [];
for i = 1:size(Xw,1)
    Pc = R*Xw(i,:)' + t;
    Xp = Pc(1); Yp = Pc(2); Zp = Pc(3);
    u = K(1,1)*Xp/Zp + K(1,3);
    v = K(2,2)*Yp/Zp + K(2,3);
    r = [r; x2d(i,1)-u; x2d(i,2)-v];
end
end

使用；

cpp 复制代码

% 生成测试
Xw = rand(20,3)*5;
R_gt = eye(3);
t_gt = [0; 0; 5];
K = [800 0 320;
     0 800 240;
     0   0   1];

% 投影生成 2D 点
x2d = zeros(20,2);
for i = 1:20
    Pc = R_gt * Xw(i,:)' + t_gt;
    x2d(i,1) = 800*Pc(1)/Pc(3) + 320;
    x2d(i,2) = 800*Pc(2)/Pc(3) + 240;
end

% 启动 PnP-LM
[R, t] = pnp_LM(Xw, x2d, K)

算法	稳定性	精度	是否需要初值
P3P	中	中	不需要
EPnP	强	中等	不需要
EPnP + LM	最强	最高	EPnP 初值