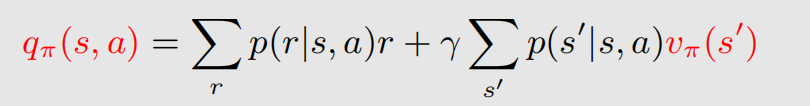贝尔曼公式(Bellman equation)
- [1 状态价值(State value)](#1 状态价值(State value))
-
- [1.1 使用定义计算回报](#1.1 使用定义计算回报)
- [1.2 使用贝尔曼公式计算回报](#1.2 使用贝尔曼公式计算回报)
- [1.3 状态价值函数的概念](#1.3 状态价值函数的概念)
- [2 贝尔曼公式(Bellman equation)](#2 贝尔曼公式(Bellman equation))
-
- [2.1 贝尔曼公式的推导](#2.1 贝尔曼公式的推导)
- [2.2 贝尔曼公式的矩阵向量形式](#2.2 贝尔曼公式的矩阵向量形式)
- [2.3 策略评价](#2.3 策略评价)
- [3 动作价值(Action value)](#3 动作价值(Action value))
- [4 总结](#4 总结)
1 状态价值(State value)
1.1 使用定义计算回报
上次课说到,回报(return)是轨迹的奖励(reward)之和(或者加权之和),我们可以以此评价轨迹所对应的策略的好坏。
如果在一个 2×2 的网格空间中,起点为 s1,有以下三种策略,现在要评估三种策略的好坏(这里假定网格任务是持续性任务,即到达终点后并不算游戏结束,而是原地打转)。
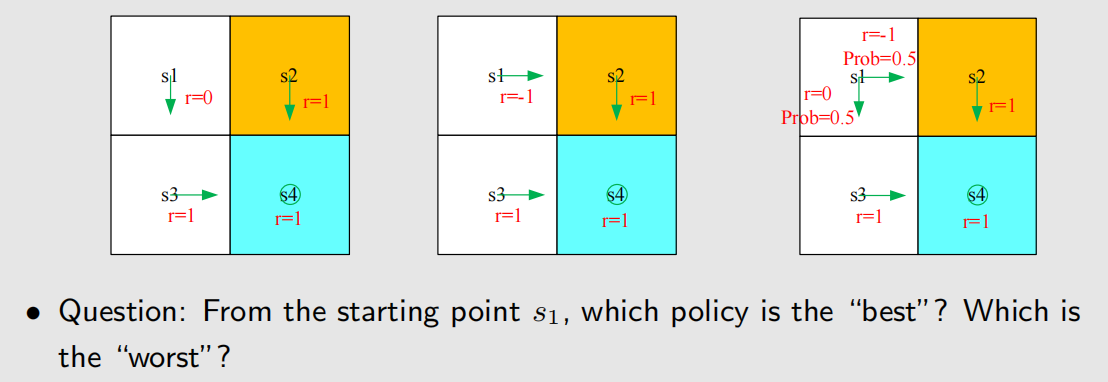
假设折扣率为 γ \gamma γ,三种策略的折扣回报为:
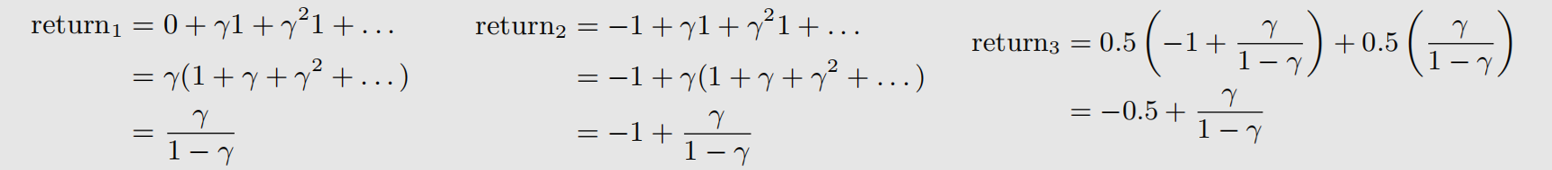
return1 和 return2 使用了等比数列求和公式,return3 则是 return1 和 return2 的加权。准确地来说,return3 并不是回报,而是状态价值(后面会介绍)。
根据上述表达式,有:return1 > return3 > return2。所以策略1最优,策略3次之,策略2最差,这和我们的直觉相符,因为我们的直觉告诉我们,策略2要穿越禁区,因此扣分最多。
1.2 使用贝尔曼公式计算回报
假如在 2×2 的网格世界中,采用以下策略:
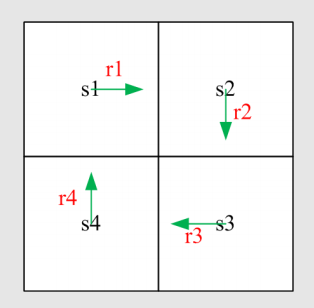
通过折扣回报的定义,可以得到:
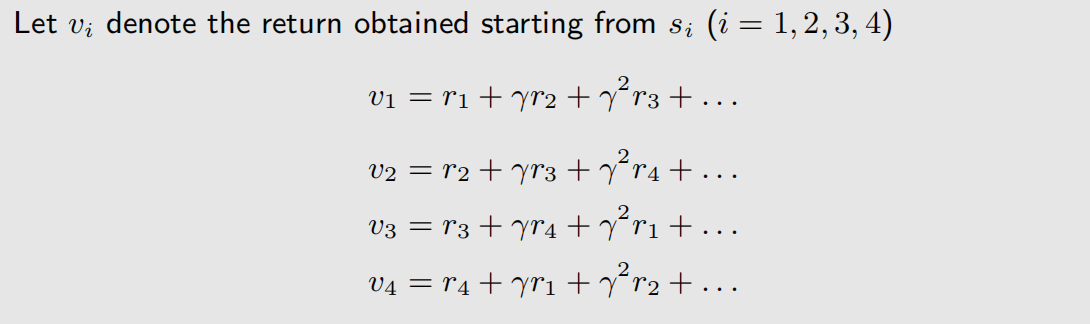
还可以通过各个状态之间的关系,得到:

Bootstrapping 的意思是从自身出发,不断迭代,左脚踩右脚,然后右脚踩左脚,最后上天!
将上面的式子写成向量和矩阵的形式,有:

此即为贝尔曼公式(Bellman Equation)。所谓贝尔曼公式,其实就是表示智能体在不同状态之间的关系的公式。
左脚踩右脚上天,也不是不可能,上面有4个式子4个未知数,那么就可以解方程: v = ( I − γ P ) − 1 r \mathbf{v} = (I-\gamma P)^{-1}\mathbf{r} v=(I−γP)−1r。这里 ∣ I − γ P ∣ = 1 + γ + γ 2 + γ 3 ≠ 0 \left | I-\gamma P \right | =1+\gamma+\gamma^2+\gamma^3 \ne 0 ∣I−γP∣=1+γ+γ2+γ3=0,因此 I − γ P I-\gamma P I−γP 可逆。
1.3 状态价值函数的概念
假设 t 时刻的状态为 S t S_t St,此时采取的动作为 A t A_t At,获得了奖励 R t + 1 R_{t+1} Rt+1,状态变成了 S t + 1 S_{t+1} St+1,用下面表达式来表示:

这里 S t S_t St、 A t A_t At、 R t + 1 R_{t+1} Rt+1 都是随机变量,因此都是大写,也都可以求期望。
上面的表达式中,存在三种概率,分别对应: A t A_t At、 R t + 1 R_{t+1} Rt+1、 S t + 1 S_{t+1} St+1,它们的概率分布分别为(这里假设所有的概率分布表达式都是已知的):

对于多步轨迹的表示方式为:
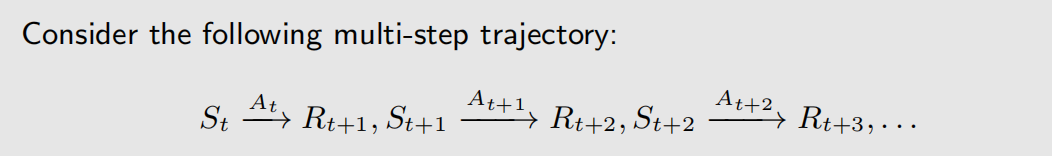
折扣回报率为:
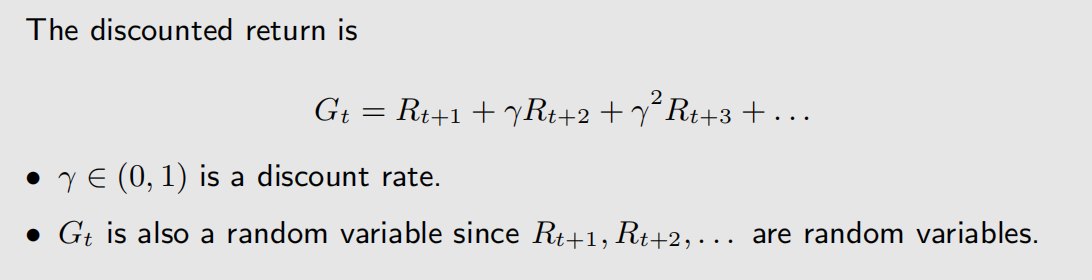
状态价值函数(state-value function,state value)则是 G t G_t Gt 的期望值,即:

状态价值函数和当前状态 s s s、策略 π \pi π有关,可以认为它是 s s s 和 π \pi π 的函数,即 υ ( s , π ) \upsilon (s, \pi) υ(s,π)。一个状态如果它的 state vlue 数值高,说明在状态转移过程中,智能体往这个状态走是值得的。如果某个人的工作步入正轨,那么他的状态价值函数是越来越高的。
状态价值(state value)和回报(return)有什么区别?回报是对具体的某一条轨迹而言的,而状态价值则是对所有可能性的期望,它是对多条轨迹的加权平均。如果从某个状态出发,只能得到一条轨迹,所有的随机性都被消除了,那么回报和状态价值就是相同的。
回到1.1节的例子,我们求的其实是状态价值:
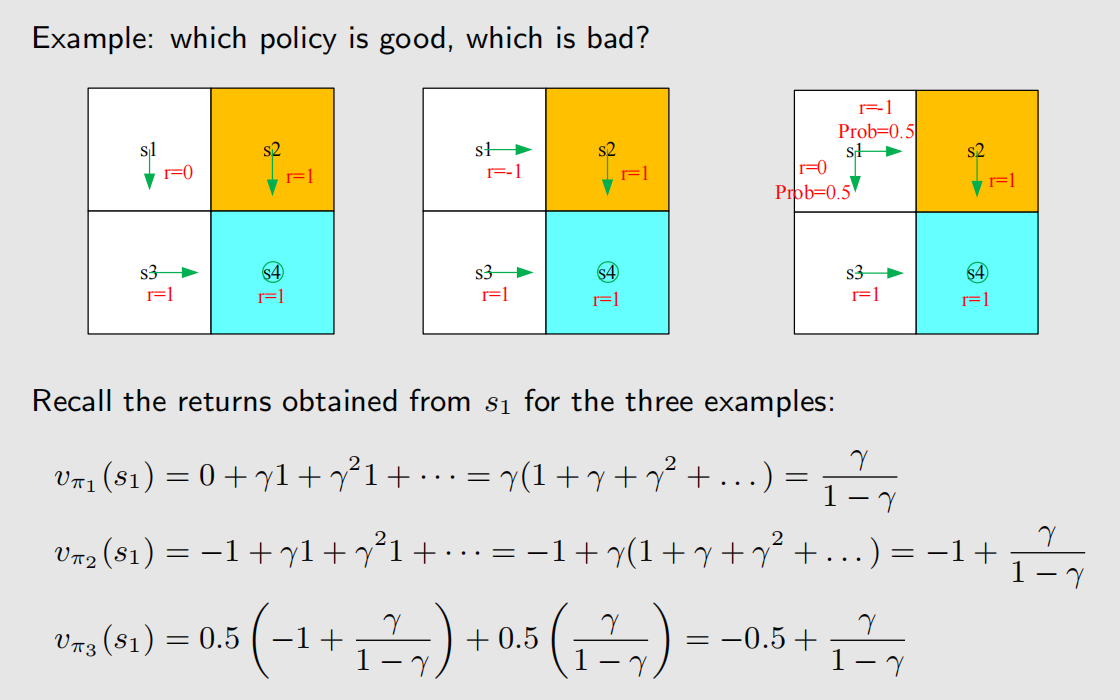
根据计算得到的 state value,可以判断哪个策略最好。
2 贝尔曼公式(Bellman equation)
2.1 贝尔曼公式的推导

可以看到, υ π ( s ) \upsilon _{\pi}(s) υπ(s) 被分成了两项,两项都是条件期望,第一项是瞬时的奖励,不需要折扣率,第二项是未来的回报,需要乘折扣率。
我们先算第一项,它表示 t 时刻为 s s s 时, R t + 1 R_{t+1} Rt+1 的数学期望是多少。在状态 s s s 的情况下,有多个动作可以去做,我们要计算每个动作做完之后 R t + 1 R_{t+1} Rt+1 的均值,即 E [ R t + 1 ∣ S t = s , A t = a ] \mathbb{E} [R_{t+1}|S_t=s,A_t=a] E[Rt+1∣St=s,At=a]。因此可以有下面的表达式:
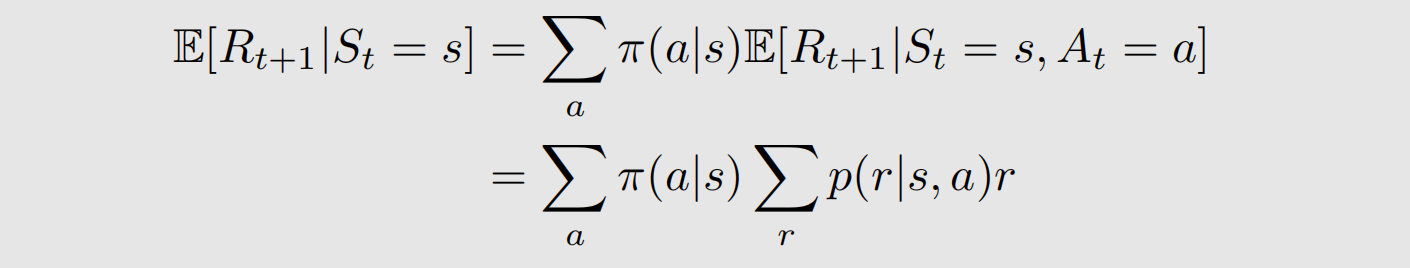
接下来是第二项,它表示从 t 时刻出发,得到的 t+1 时刻的折扣回报。t 时刻从状态 s s s 出发,那么在第 t+1 时刻的状态存在多种可能,这里要计算每一种可能状态 s ′ s' s′的数学期望,即 E [ G t + 1 ∣ S t = s , S t + 1 = s ′ ] \mathbb{E} [G_{t+1}|S_t=s,S_{t+1}=s'] E[Gt+1∣St=s,St+1=s′],根据马尔可夫过程的遗忘特性,有:
E [ G t + 1 ∣ S t = s , S t + 1 = s ′ ] = E [ G t + 1 ∣ S t + 1 = s ′ ] = υ π ( s ′ ) \mathbb{E} [G_{t+1}|S_t=s,S_{t+1}=s']=\mathbb{E} [G_{t+1}|S_{t+1}=s']=\upsilon _{\pi}(s') E[Gt+1∣St=s,St+1=s′]=E[Gt+1∣St+1=s′]=υπ(s′)
此外,从状态 s s s 转移到状态 s ′ s' s′,有多种动作可以做,根据全概率公式,有: p ( s ′ ∣ s ) = ∑ a p ( s ′ ∣ s , a ) π ( a ∣ s ) p(s'|s)=\sum_{a}^{} p(s'|s,a)\pi (a|s) p(s′∣s)=∑ap(s′∣s,a)π(a∣s)。综上,第二项为:

我们把两项一起写,有:
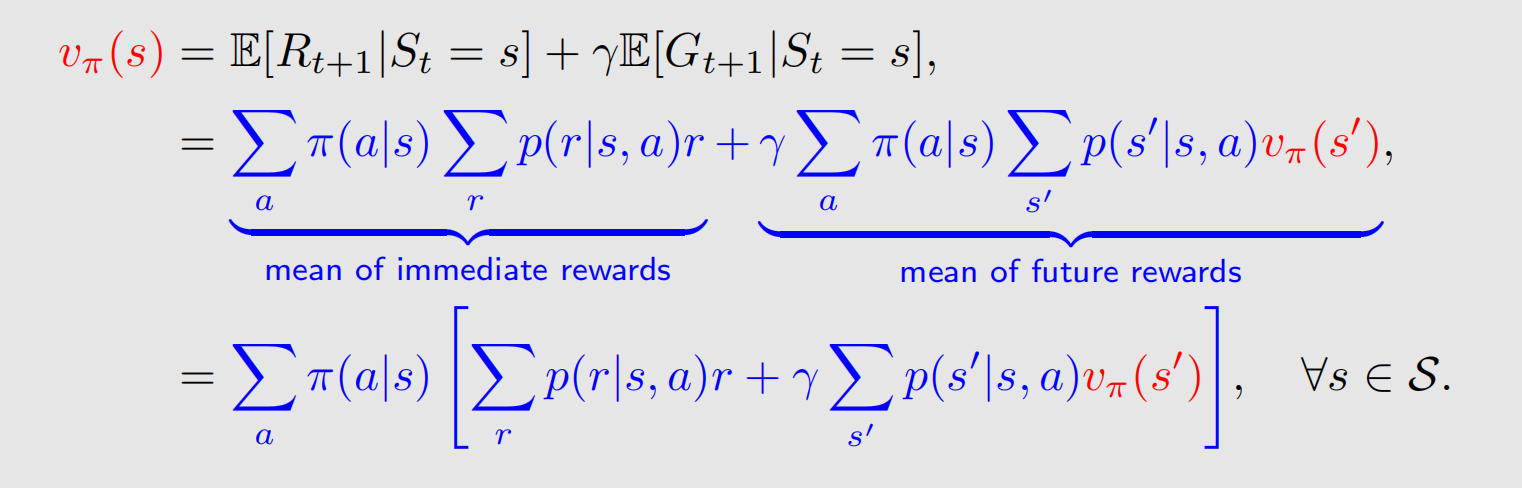
这就是贝尔曼公式,它表达了不同状态下 state value 的相互关系。其中,为了提公因子,我们改变了第二项的求和顺序。这个式子对状态空间中所有的状态都成立的,如果有n个状态,那么就会有n个这样的式子,通过这些式子就能把 state value 求解出来。
下面有个案例:

上面通过贝尔曼公式计算得到的状态价值函数,和根据直接观察得到的结果一致。类似的,有:
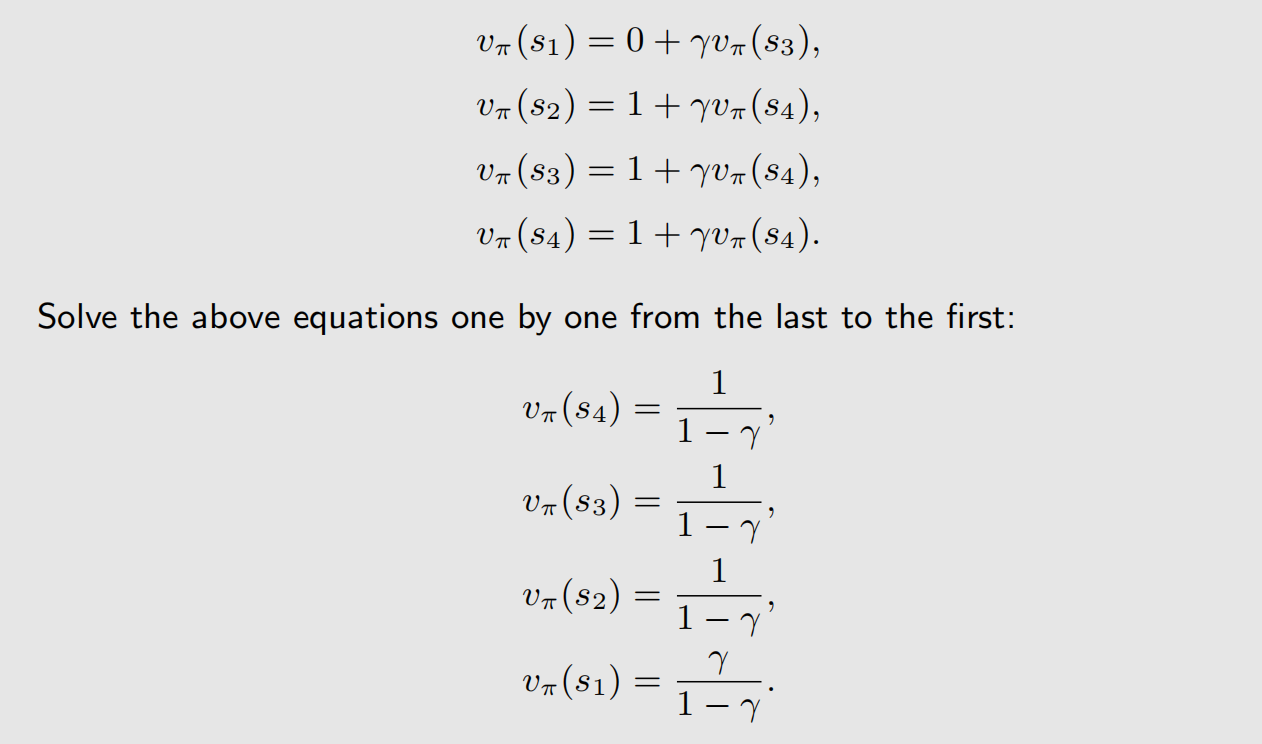
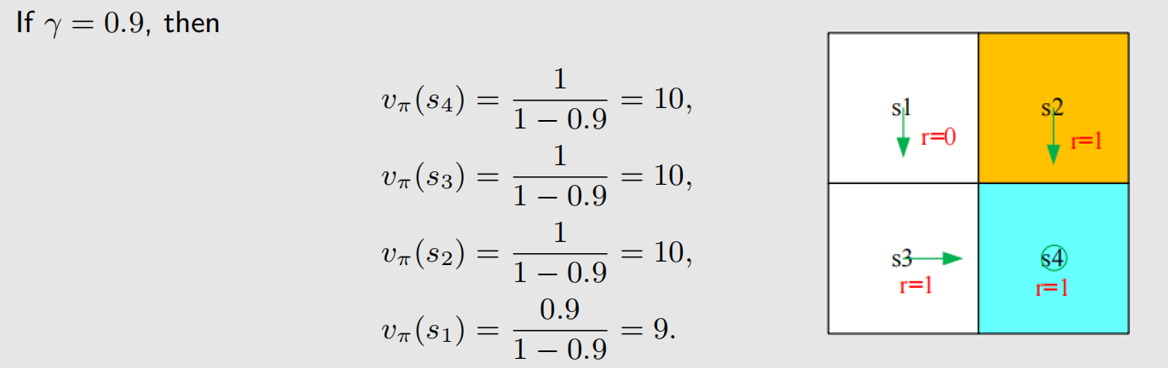
可以看到,state value 高的地方,要么是目标位置,要么就是和目标位置离得近的位置。前面说到,state value 可以用来评价策略,好的策略应该是人往高处走。
2.2 贝尔曼公式的矩阵向量形式
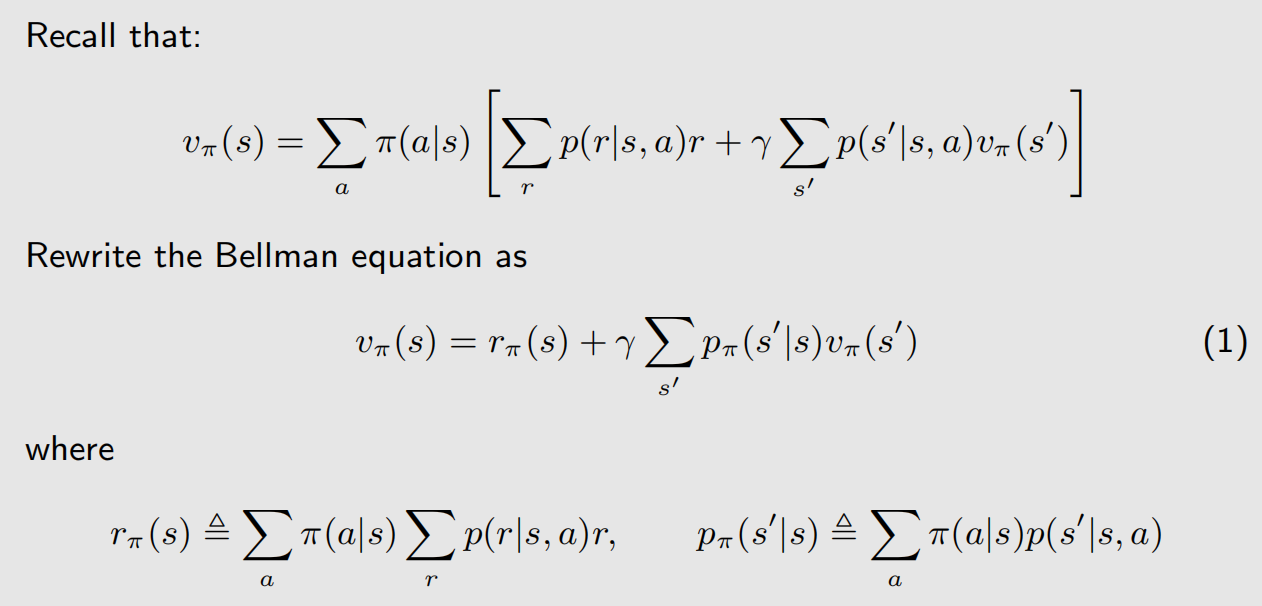
r π ( s ) r_{\pi}(s) rπ(s) 是瞬时收益, p π ( s ′ ∣ s ) p_{\pi}(s'|s) pπ(s′∣s) 是状态转移概率,这两个符号都有下表 π \pi π。

这里 P π P_{\pi} Pπ 是状态转移矩阵,第 i 行第 j 列表示从状态 s i s_i si 转移到状态 s j s_j sj 的概率。
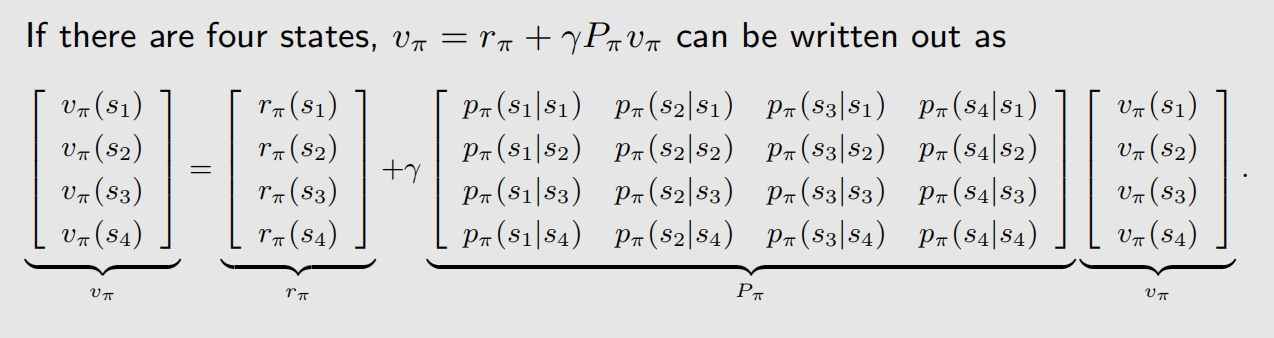
接下来我们看两个示例,根据上面的形式,我们可以根据策略,很轻松地写出贝尔曼式子:
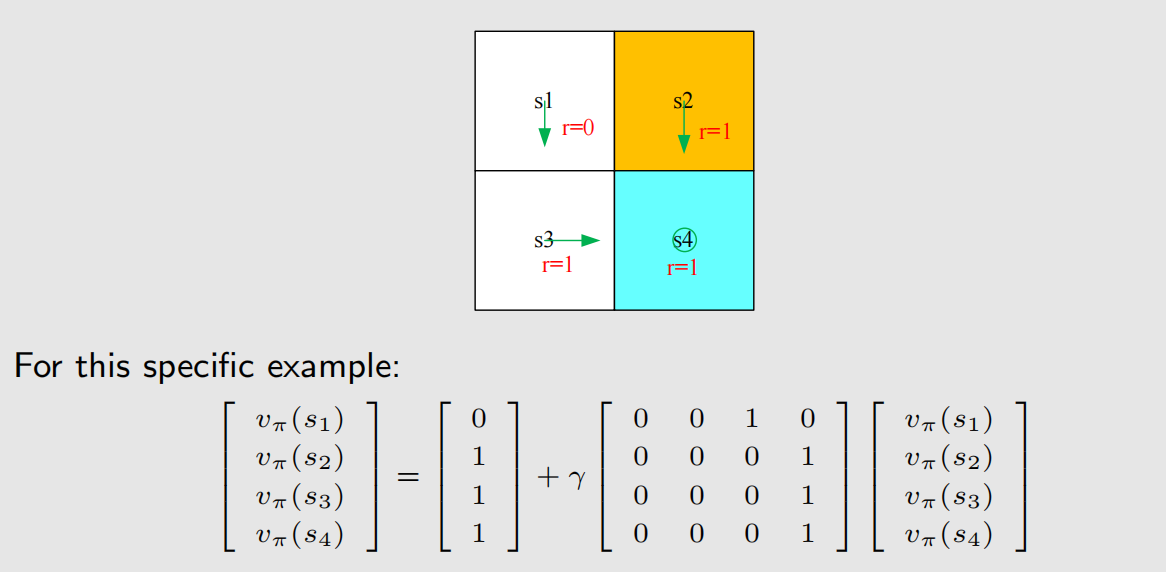
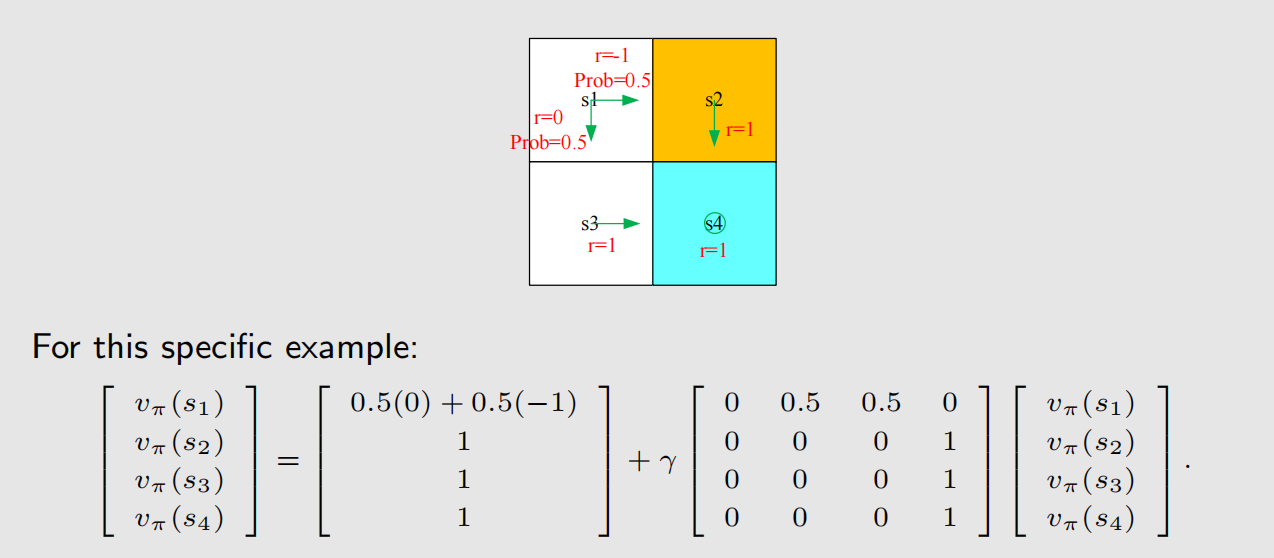
2.3 策略评价
给定一个策略,然后算出它的 state value,即求解贝尔曼公式,这个过程就叫策略评价。

从上面的截图可以看到,贝尔曼公式的求解有两种方式,一种是通过求逆矩阵,另一种是通过迭代。如果状态比较多,求逆矩阵比较困难,所以一般情况下都是通过迭代来近似求解,它利用数列的收敛特性来得到结果,如果学过《数值计算方法》,那么对这种方式会比较熟悉。
迭代算法的证明如下图所示,选择看,有时间就看,没时间算了。

3 动作价值(Action value)
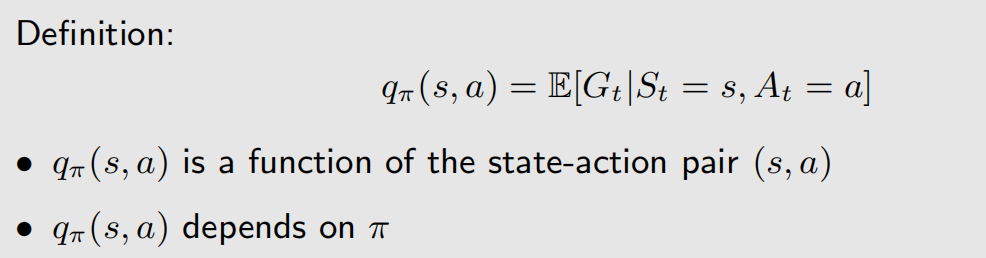
q π ( s , a ) q_{\pi}(s,a) qπ(s,a) 就是动作价值函数(Action-value function,action value),action value 常用来评估某个动作的好坏,它与 state value 的关系如下:
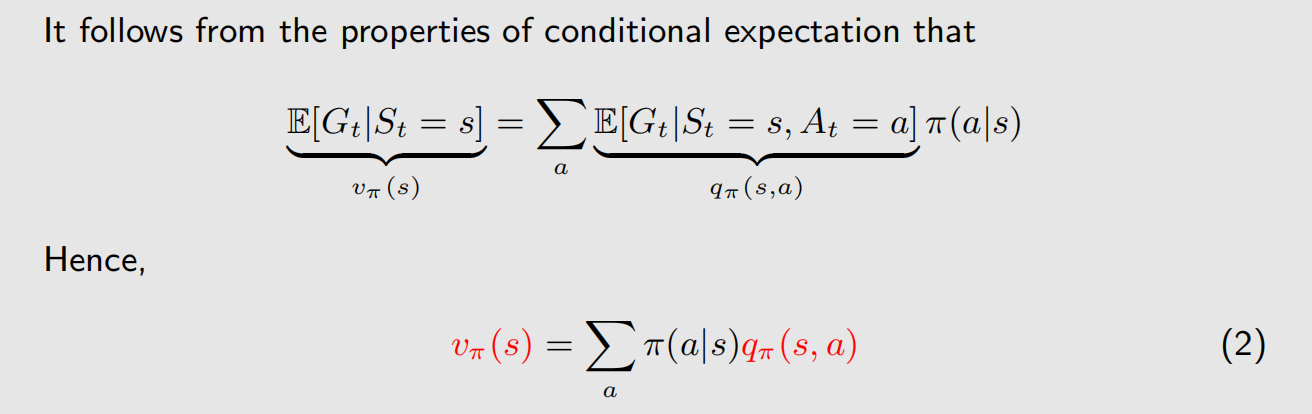

从上面的截图可以看到,(2)式是根据 action value 求 state value,(4)式是根据 state value 求 action value。
(4)式的结构表示 action value 可以根据瞬时奖励和未来奖励加权得到,我们用一个示例来加强对 action value 的理解:
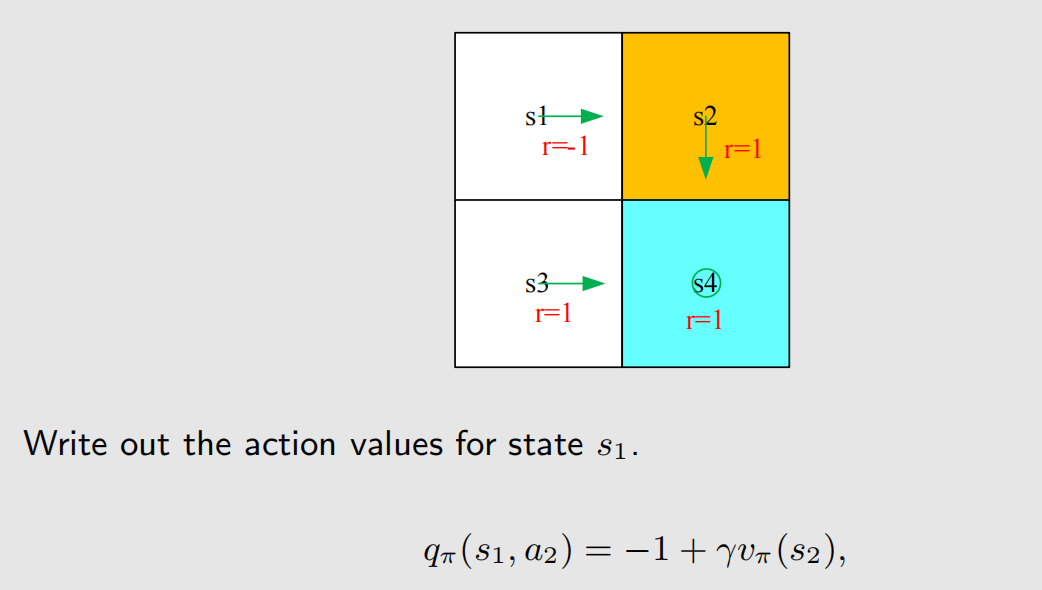
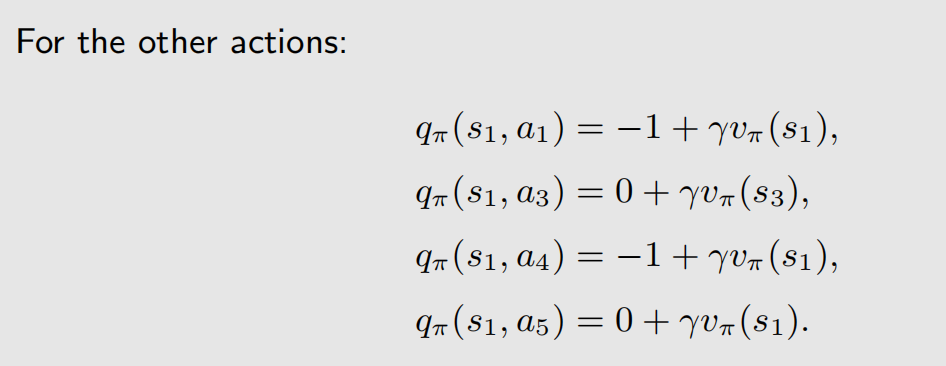
q π ( s , a 1 ) q_{\pi}(s,a_1) qπ(s,a1) 不是0,虽然 π ( a 1 ∣ s 1 ) \pi(a_1|s_1) π(a1∣s1) 是0,但 q π ( s , a 1 ) q_{\pi}(s,a_1) qπ(s,a1) 是假定 a 1 a_1 a1 已经发生了, q π ( s , a 3 ) q_{\pi}(s,a_3) qπ(s,a3)、 q π ( s , a 4 ) q_{\pi}(s,a_4) qπ(s,a4)、 q π ( s , a 5 ) q_{\pi}(s,a_5) qπ(s,a5) 也是同样的道理。
4 总结
这节课公式非常多,但核心的内容可以用一张PPT概括:

我觉得这张PPT还少了一个公式,就是根据 state value 计算 action value 的公式,补充如下: