
这一章介绍最优策略与贝尔曼最优公式
贝尔曼最优公式是贝尔曼公式的一个特殊情况
学习的过程中重点关注两个概念与一个公式
这两个概念是最优状态值和最优策略
一个公式就是贝尔曼最优公式


第一件事是求解贝尔曼最优公式得到状态值,从而得到action value

求解出来后,发现一个问题,就是当前这个策略实际上是不太好的,因为在s1s_1s1状态下他向右进入了禁止区域
发现a3a_3a3对应的action value是最大的


问题:
这种最优的策略是否存在?
这种最优的策略是否是唯一的?
这种最优的策略是确定性的还是非确定性的

在常规的贝尔曼公式前面加上一个max,这个时候π\piπ就是给定的
需要求解这个最优化问题,求解出来π\piπ,然后带回到公式里面去,


这个式子里面有一个未知量v,然后还需要求解一个π\piπ ,






把maxπmax_{\pi}maxπ改写为一个函数f(v)
首先要介绍压缩映射定理 和 不动点



压缩映射定理 告诉我们三个重要的结论
第一是:不关心f函数究竟是什么?只要它满足这个定理,它一定存在一个不动点,满足f(x*)=x*
第二是:这个不动点是唯一存在的
第三是:我知道是如何求解的






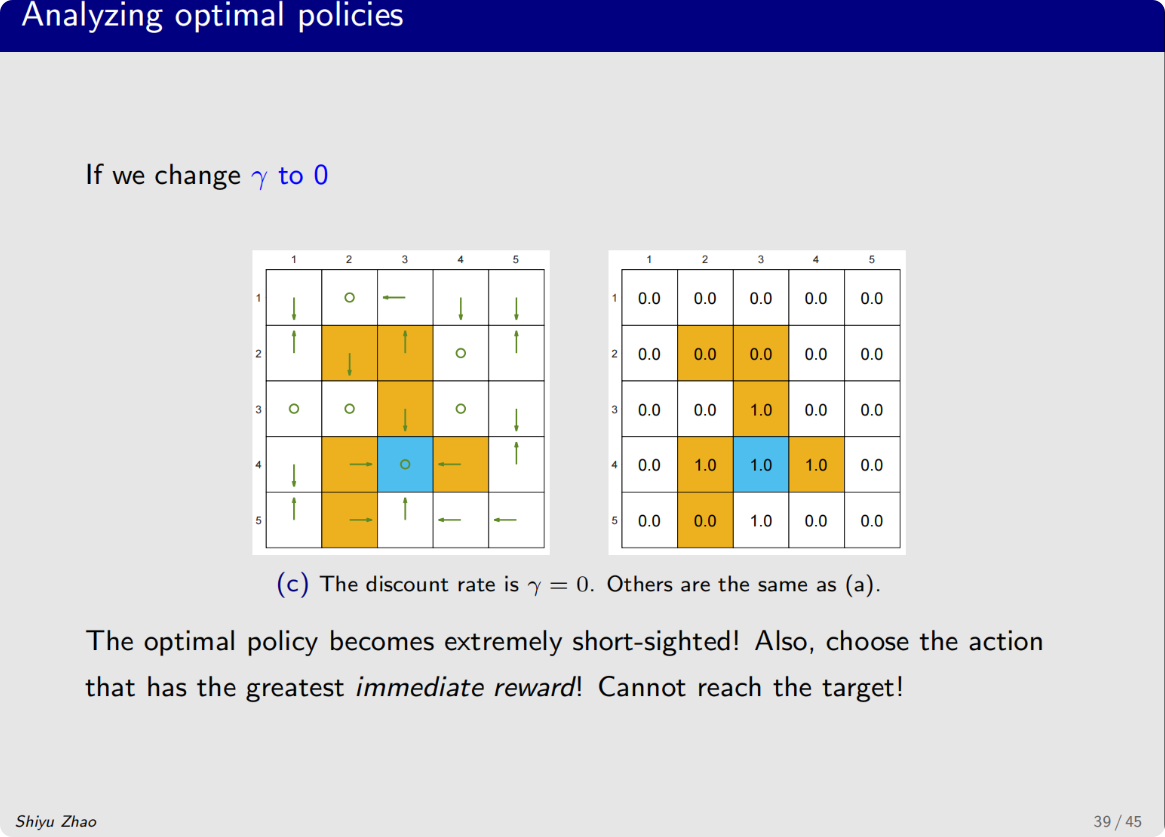
什么样的因素决定了最优策略
奖励的设计、系统模型



仿射变换
不看action value的绝对值而是相对值