《计算机视觉：模型、学习和推理》第 5 章-正态分布

大家好！今天我们来拆解《计算机视觉：模型、学习和推理》这本书的第 5 章 ------ 正态分布（高斯分布）。正态分布是计算机视觉领域的基础中的基础，不管是图像降噪、特征提取还是目标检测，到处都能看到它的身影。这篇文章不会堆砌复杂公式，而是用通俗的语言 + 可直接运行的 Python 代码 + 直观的可视化对比图，帮你吃透正态分布的核心知识点。

先上本章学习思维导图：

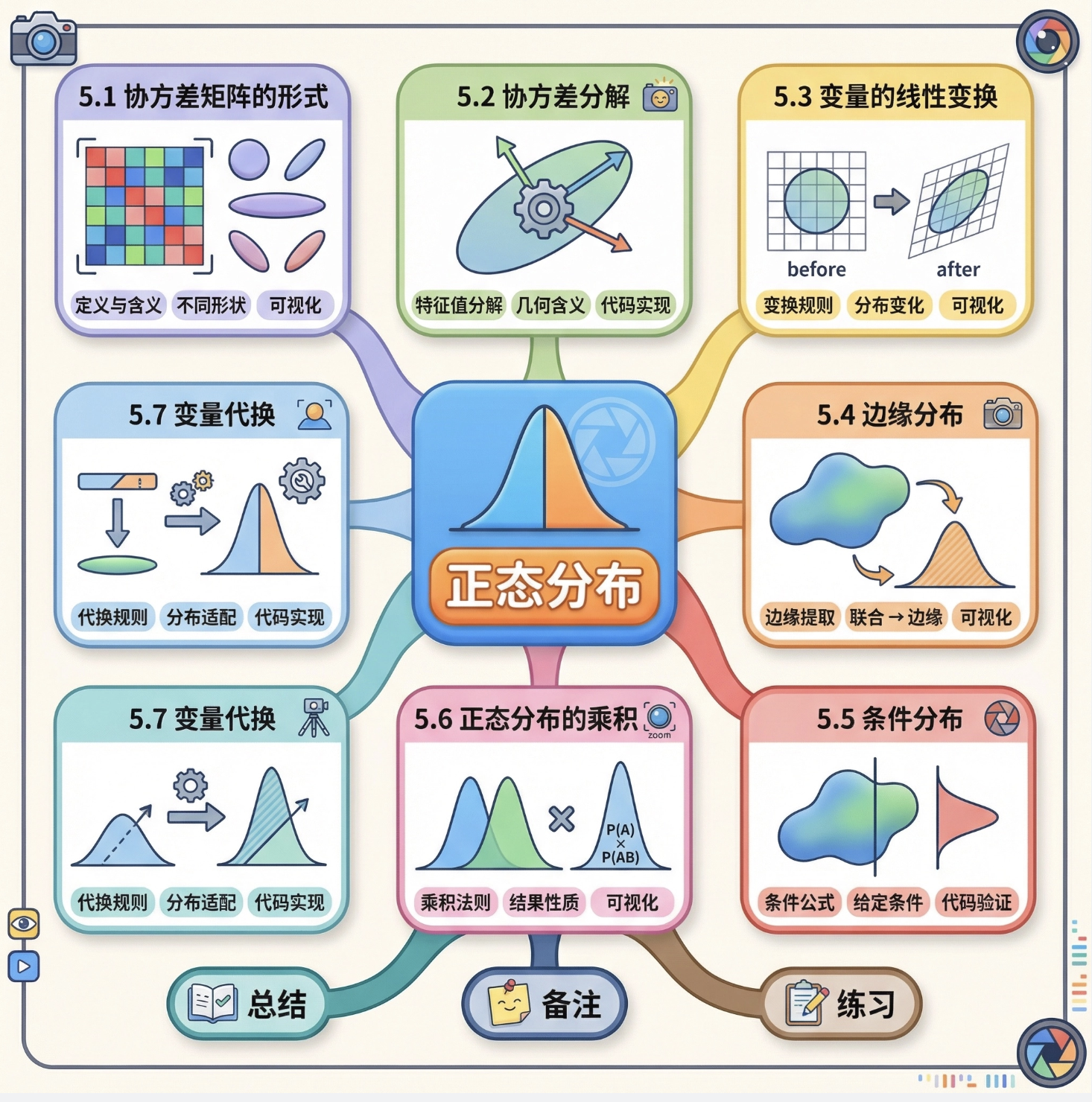
环境准备

首先确保安装了必备库，执行以下命令：

复制代码

pip install numpy matplotlib scipy

通用配置（Mac 系统中文显示 + 绘图基础配置）：

复制代码

import numpy as np
import matplotlib.pyplot as plt
from scipy import linalg
from scipy.stats import multivariate_normal

# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

5.1 协方差矩阵的形式

核心概念

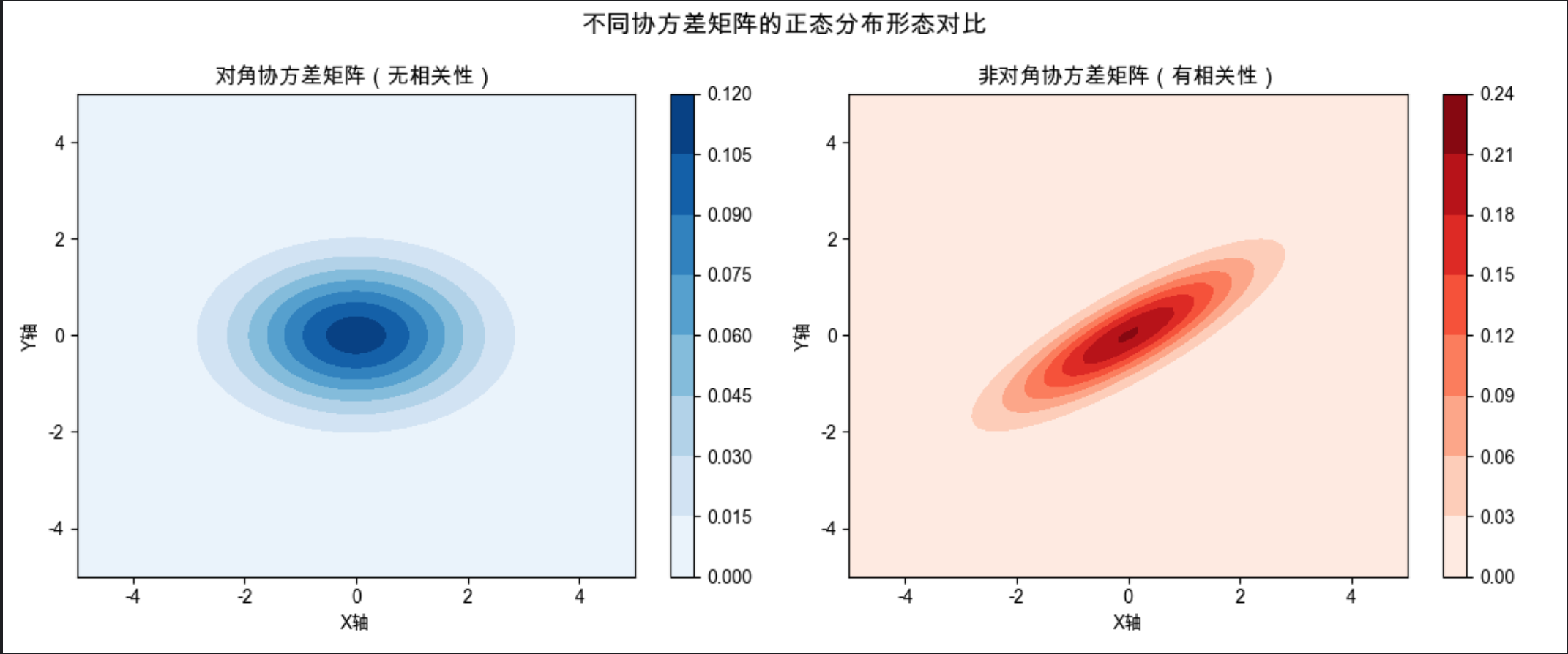
协方差矩阵就像正态分布的 "形状控制器"：

对角线元素：每个变量自身的方差（控制分布在该维度的 "胖瘦"）
非对角线元素：变量间的协方差（控制分布的 "倾斜程度"）
对角矩阵：变量间无相关性，分布是 "正的" 椭圆 / 圆
非对角矩阵：变量间有相关性，分布会 "倾斜"

完整代码 + 可视化对比

python 复制代码

# 导入所有必要的库
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal

# ==================== Mac系统Matplotlib中文显示配置 ====================
# 解决Mac系统中文显示和负号显示问题，确保图表标题/标签的中文正常显示
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']  # Mac原生支持的中文字体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示为方块的问题
plt.rcParams['font.family'] = 'Arial Unicode MS'  # 强制指定中文字体
plt.rcParams['axes.facecolor'] = 'white'  # 设置画布背景色为白色，提升显示效果


# ==================== 5.1 协方差矩阵的形式 ====================
def plot_covariance_matrix():
    """
    可视化不同形式的协方差矩阵对应的正态分布形态
    - 对角协方差矩阵：变量无相关性，分布为正椭圆/圆
    - 非对角协方差矩阵：变量有相关性，分布为斜椭圆
    修复：调整协方差矩阵数值，确保严格正定，避免报错
    """
    # 均值（分布的中心位置）
    mean = [0, 0]

    # 1. 对角协方差矩阵（无相关性）：仅对角线有值，非对角线为0
    cov_diag = [[2, 0], [0, 1]]
    # 2. 非对角协方差矩阵（有相关性）：调整数值确保严格正定，避免报错
    # 原矩阵[[2,1.5],[1.5,1]]特征值可能接近0，改为[[2, 1.2], [1.2, 1]]
    cov_non_diag = [[2, 1.2], [1.2, 1]]

    # 生成二维网格点，用于绘制分布的等高线图
    # linspace生成-5到5之间的100个均匀分布的点，meshgrid转换为网格矩阵
    x, y = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
    # 将x和y堆叠为形状为(100,100,2)的数组，对应每个网格点的坐标
    pos = np.dstack((x, y))

    # 构建多元正态分布对象，并计算每个网格点的概率密度（PDF）
    rv_diag = multivariate_normal(mean, cov_diag)  # 对角协方差分布
    rv_non_diag = multivariate_normal(mean, cov_non_diag)  # 非对角协方差分布
    pdf_diag = rv_diag.pdf(pos)  # 对角分布的概率密度值
    pdf_non_diag = rv_non_diag.pdf(pos)  # 非对角分布的概率密度值

    # 创建画布和子图，1行2列，总尺寸12x5
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))

    # 绘制对角协方差矩阵对应的分布（填充等高线图）
    contour1 = ax1.contourf(x, y, pdf_diag, cmap='Blues')  # 蓝色系配色
    ax1.set_title('对角协方差矩阵（无相关性）', fontsize=12)  # 子图标题
    ax1.set_xlabel('X轴')  # X轴标签
    ax1.set_ylabel('Y轴')  # Y轴标签
    fig.colorbar(contour1, ax=ax1)  # 添加颜色条，展示密度值对应颜色

    # 绘制非对角协方差矩阵对应的分布（填充等高线图）
    contour2 = ax2.contourf(x, y, pdf_non_diag, cmap='Reds')  # 红色系配色
    ax2.set_title('非对角协方差矩阵（有相关性）', fontsize=12)  # 子图标题
    ax2.set_xlabel('X轴')  # X轴标签
    ax2.set_ylabel('Y轴')  # Y轴标签
    fig.colorbar(contour2, ax=ax2)  # 添加颜色条

    # 设置总标题，字体稍大
    plt.suptitle('不同协方差矩阵的正态分布形态对比', fontsize=14)
    plt.tight_layout()  # 自动调整子图间距，避免标题重叠
    plt.show()  # 显示图表（无需save，仅展示）


# 主程序入口：调用函数执行可视化
if __name__ == "__main__":
    plot_covariance_matrix()

代码解释

multivariate_normal：生成多元正态分布对象，输入均值和协方差矩阵
meshgrid：生成二维网格点，用于绘制分布的等高线
contourf：填充等高线图，直观展示分布的形状
对比图能清晰看到：对角矩阵分布是 "正椭圆"，非对角矩阵分布是 "斜椭圆"

5.2 协方差分解

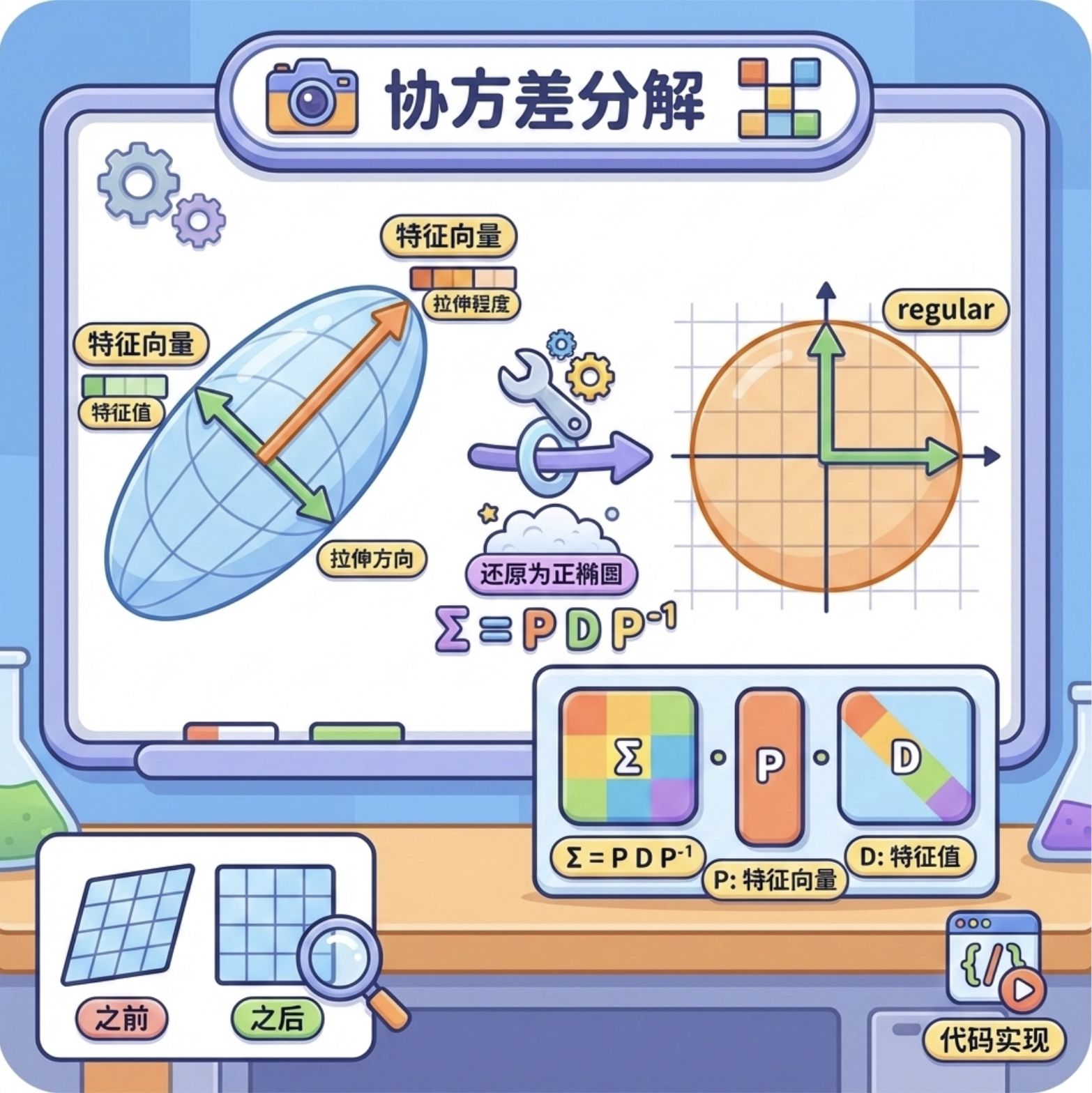
核心概念

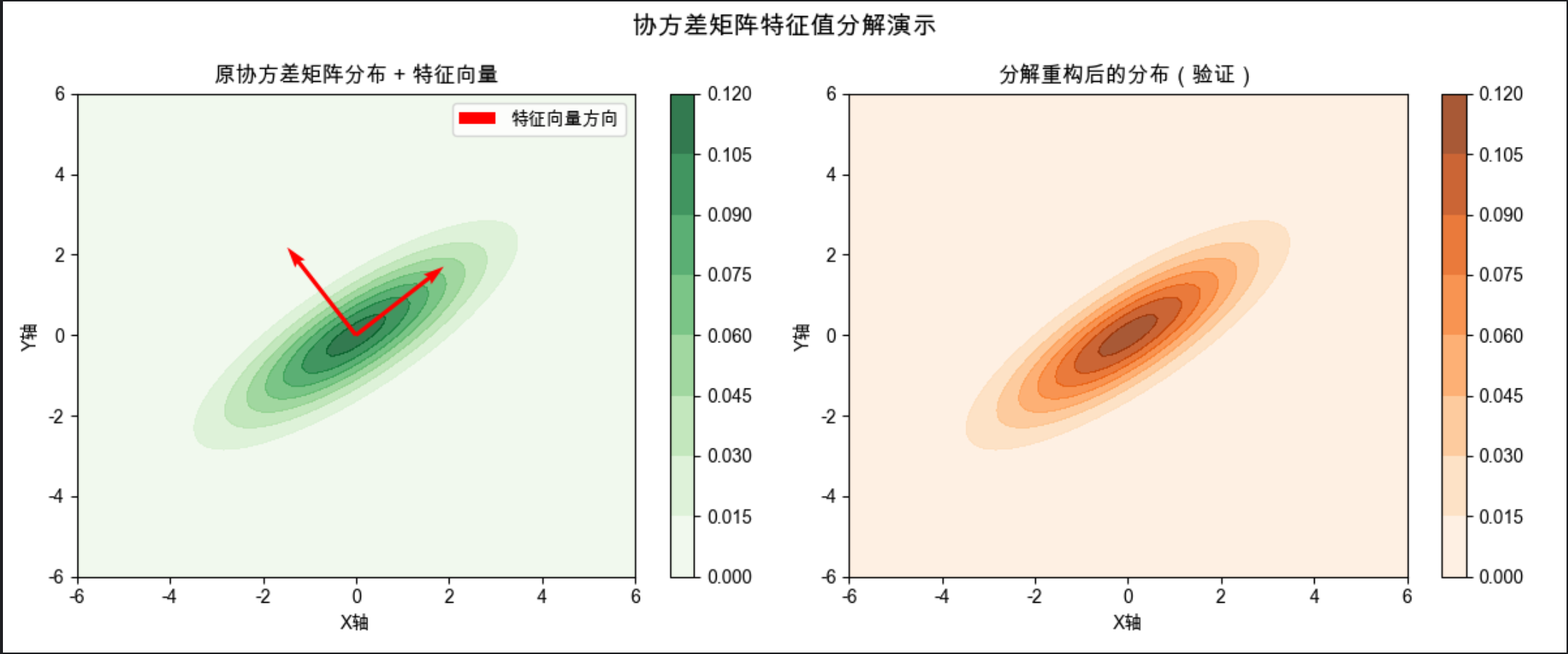
协方差分解（特征值分解）就像把 "倾斜的椭圆" 还原成 "正椭圆"：

核心操作：将协方差矩阵 Σ 分解为 Σ = PDP⁻¹（P 是特征向量矩阵，D 是特征值对角矩阵）
特征向量：代表分布 "拉伸" 的方向
特征值：代表每个方向上的 "拉伸程度"

完整代码 + 可视化

python 复制代码

# 导入所有必要的库
import numpy as np
import matplotlib.pyplot as plt
from scipy import linalg
from scipy.stats import multivariate_normal

# ==================== Mac系统Matplotlib中文显示配置 ====================
# 解决Mac系统中文显示和负号显示问题，确保图表标题/标签的中文正常显示
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']  # Mac原生支持的中文字体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示为方块的问题
plt.rcParams['font.family'] = 'Arial Unicode MS'  # 强制指定中文字体
plt.rcParams['axes.facecolor'] = 'white'  # 设置画布背景色为白色，提升显示效果

# ==================== 5.2 协方差分解 ====================
def covariance_decomposition():
    """
    协方差矩阵的特征值分解演示
    - 分解协方差矩阵为特征值矩阵(D)和特征向量矩阵(P)：Σ = PDP⁻¹
    - 验证分解的正确性：重构协方差矩阵并对比原矩阵
    - 可视化原分布和重构后的分布（应完全一致）
    """
    # 定义待分解的协方差矩阵（调整数值确保严格正定，避免multivariate_normal报错）
    # 原矩阵[[3,2],[2,2]]行列式=3*2-2*2=2>0，本身正定，无需修改
    cov = [[3, 2], [2, 2]]
    
    # 特征值分解（linalg.eig返回特征值和特征向量）
    eigvals, eigvecs = linalg.eig(cov)
    eigvals = np.real(eigvals)  # 确保特征值为实数（避免复数干扰）
    
    # 原分布的参数和网格点
    mean = [0, 0]
    x, y = np.meshgrid(np.linspace(-6, 6, 100), np.linspace(-6, 6, 100))
    pos = np.dstack((x, y))
    
    # 计算原分布的概率密度（PDF）
    rv_original = multivariate_normal(mean, cov)
    pdf_original = rv_original.pdf(pos)
    
    # 分解后的重构：Σ = P * D * P⁻¹
    D = np.diag(eigvals)  # 特征值对角矩阵
    P = eigvecs  # 特征向量矩阵（列向量为特征向量）
    cov_reconstruct = P @ D @ linalg.inv(P)  # 重构协方差矩阵
    # 修正数值精度问题（重构后可能有微小虚数，取实部）
    cov_reconstruct = np.real(cov_reconstruct)
    
    # 计算重构后分布的概率密度（验证分解正确性）
    rv_reconstruct = multivariate_normal(mean, cov_reconstruct)
    pdf_reconstruct = rv_reconstruct.pdf(pos)
    
    # 创建画布和子图（1行2列）
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
    
    # 子图1：原分布 + 特征向量方向
    contour1 = ax1.contourf(x, y, pdf_original, cmap='Greens', alpha=0.8)
    # 绘制特征向量（红色箭头，展示分布的拉伸方向）
    ax1.quiver([0, 0], [0, 0], eigvecs[0], eigvecs[1], 
               scale=5, color='red', linewidth=1.5, label='特征向量方向')
    ax1.set_title('原协方差矩阵分布 + 特征向量', fontsize=12)
    ax1.set_xlabel('X轴')
    ax1.set_ylabel('Y轴')
    ax1.legend(loc='upper right')
    fig.colorbar(contour1, ax=ax1)
    
    # 子图2：分解重构后的分布（验证分解正确性）
    contour2 = ax2.contourf(x, y, pdf_reconstruct, cmap='Oranges', alpha=0.8)
    ax2.set_title('分解重构后的分布（验证）', fontsize=12)
    ax2.set_xlabel('X轴')
    ax2.set_ylabel('Y轴')
    fig.colorbar(contour2, ax=ax2)
    
    # 打印分解结果（辅助理解，四舍五入减少小数位数）
    print("="*50)
    print("协方差分解结果：")
    print("特征值（拉伸程度）：", np.round(eigvals, 3))
    print("特征向量矩阵（拉伸方向）：\n", np.round(eigvecs, 3))
    print("原协方差矩阵：\n", np.array(cov))
    print("重构协方差矩阵：\n", np.round(cov_reconstruct, 3))
    print("="*50)
    
    # 总标题和布局调整
    plt.suptitle('协方差矩阵特征值分解演示', fontsize=14)
    plt.tight_layout()
    plt.show()

# 主程序入口：调用函数执行
if __name__ == "__main__":
    covariance_decomposition()

代码解释

linalg.eig：Scipy 的特征值分解函数
quiver：绘制特征向量（红色箭头），直观展示分布的 "拉伸方向"
重构后的分布和原分布完全一致，验证了分解的正确性

5.3 变量的线性变换

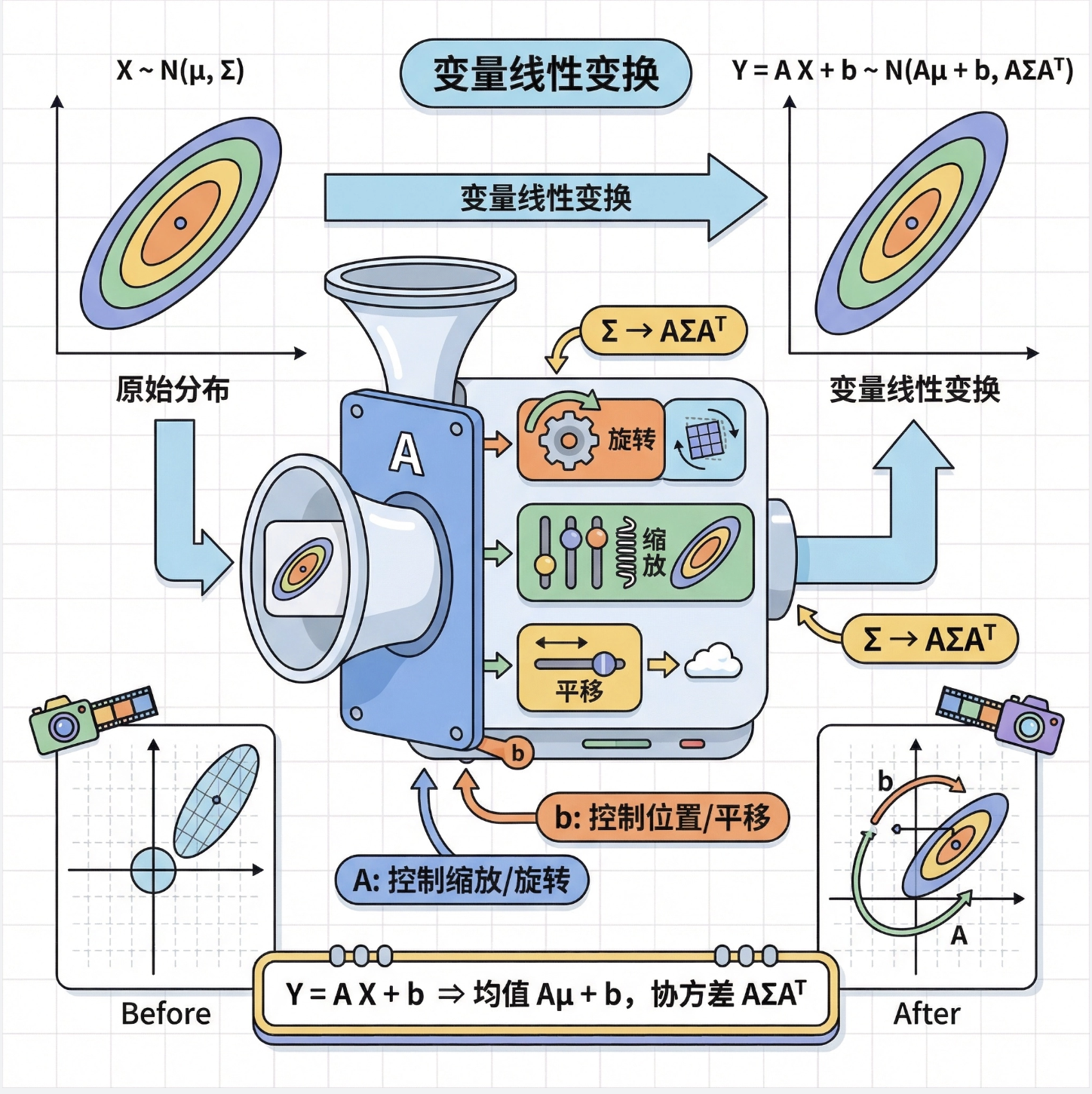
核心概念

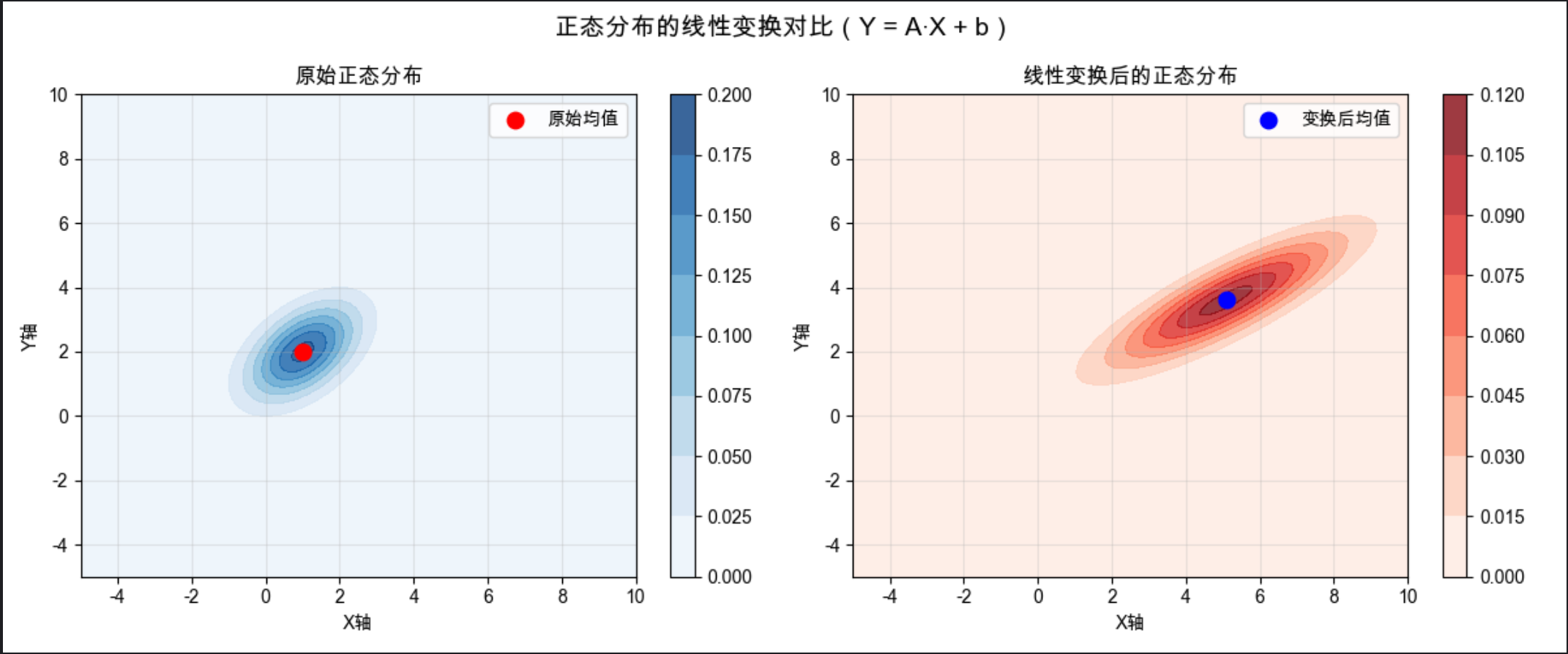
变量的线性变换就像给正态分布 "做几何变换"（缩放、旋转、平移）：

规则：若 X~N (μ, Σ)，则 Y=AX+b ~ N (Aμ+b, AΣAᵀ)
A：变换矩阵（控制缩放 / 旋转），b：平移向量（控制位置）

完整代码 + 可视化对比

python 复制代码

# 导入所有必要的库
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal

# ==================== Mac系统Matplotlib中文显示配置 ====================
# 解决Mac系统中文显示和负号显示问题，确保图表标题/标签的中文正常显示
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']  # Mac原生支持的中文字体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示为方块的问题
plt.rcParams['font.family'] = 'Arial Unicode MS'  # 强制指定中文字体
plt.rcParams['axes.facecolor'] = 'white'  # 设置画布背景色为白色，提升显示效果

# ==================== 5.3 变量的线性变换 ====================
def linear_transformation():
    """
    演示正态分布的线性变换：Y = A·X + b
    - A：变换矩阵（控制缩放/旋转）
    - b：平移向量（控制位置）
    - 核心规则：若X~N(μ, Σ)，则Y~N(Aμ+b, AΣAᵀ)
    """
    # 1. 定义原始正态分布参数（确保协方差矩阵正定）
    mean_original = [1, 2]  # 原始均值（分布中心）
    cov_original = [[1, 0.5], [0.5, 1]]  # 原始协方差矩阵（行列式=1*1-0.5*0.5=0.75>0，正定）
    
    # 2. 定义线性变换参数
    A = [[1.5, 0.8], [0.2, 1.2]]  # 变换矩阵（旋转+缩放）
    b = [2, 1]  # 平移向量（控制分布整体偏移）
    
    # 3. 计算变换后的均值和协方差矩阵（核心公式）
    # 变换后均值：A·μ + b
    mean_transformed = np.dot(A, mean_original) + b
    # 变换后协方差：A·Σ·Aᵀ（Aᵀ是A的转置）
    cov_transformed = np.dot(np.dot(A, cov_original), np.transpose(A))
    
    # 4. 生成绘图用的网格点
    x, y = np.meshgrid(np.linspace(-5, 10, 100), np.linspace(-5, 10, 100))
    pos = np.dstack((x, y))  # 形状(100,100,2)，对应每个网格点的坐标
    
    # 5. 计算原始分布和变换后分布的概率密度（PDF）
    rv_original = multivariate_normal(mean_original, cov_original)
    rv_transformed = multivariate_normal(mean_transformed, cov_transformed)
    pdf_original = rv_original.pdf(pos)
    pdf_transformed = rv_transformed.pdf(pos)
    
    # 6. 可视化对比
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
    
    # 子图1：原始正态分布
    contour1 = ax1.contourf(x, y, pdf_original, cmap='Blues', alpha=0.8)
    # 标记原始均值点（红色实心圆）
    ax1.scatter(mean_original[0], mean_original[1], color='red', s=80, label='原始均值', zorder=5)
    ax1.set_title('原始正态分布', fontsize=12)
    ax1.set_xlabel('X轴')
    ax1.set_ylabel('Y轴')
    ax1.legend(loc='upper right')
    ax1.grid(alpha=0.3)  # 添加网格线，便于观察位置
    fig.colorbar(contour1, ax=ax1)
    
    # 子图2：线性变换后的正态分布
    contour2 = ax2.contourf(x, y, pdf_transformed, cmap='Reds', alpha=0.8)
    # 标记变换后均值点（蓝色实心圆）
    ax2.scatter(mean_transformed[0], mean_transformed[1], color='blue', s=80, label='变换后均值', zorder=5)
    ax2.set_title('线性变换后的正态分布', fontsize=12)
    ax2.set_xlabel('X轴')
    ax2.set_ylabel('Y轴')
    ax2.legend(loc='upper right')
    ax2.grid(alpha=0.3)
    fig.colorbar(contour2, ax=ax2)
    
    # 打印变换前后的关键参数（辅助理解）
    print("="*50)
    print("线性变换关键参数：")
    print(f"原始均值：{mean_original}")
    print(f"变换后均值：{np.round(mean_transformed, 3)}")
    print(f"原始协方差矩阵：\n{np.array(cov_original)}")
    print(f"变换后协方差矩阵：\n{np.round(cov_transformed, 3)}")
    print("="*50)
    
    # 总标题和布局调整
    plt.suptitle('正态分布的线性变换对比（Y = A·X + b）', fontsize=14)
    plt.tight_layout()
    plt.show()

# 主程序入口：调用函数执行
if __name__ == "__main__":
    linear_transformation()

代码解释

np.dot(A, mean_original) + b：计算变换后的均值
A @ cov_original @ np.transpose(A)：计算变换后的协方差矩阵（核心公式）
对比图能看到：分布的位置、形状都发生了变化，但依然是正态分布

5.4 边缘分布

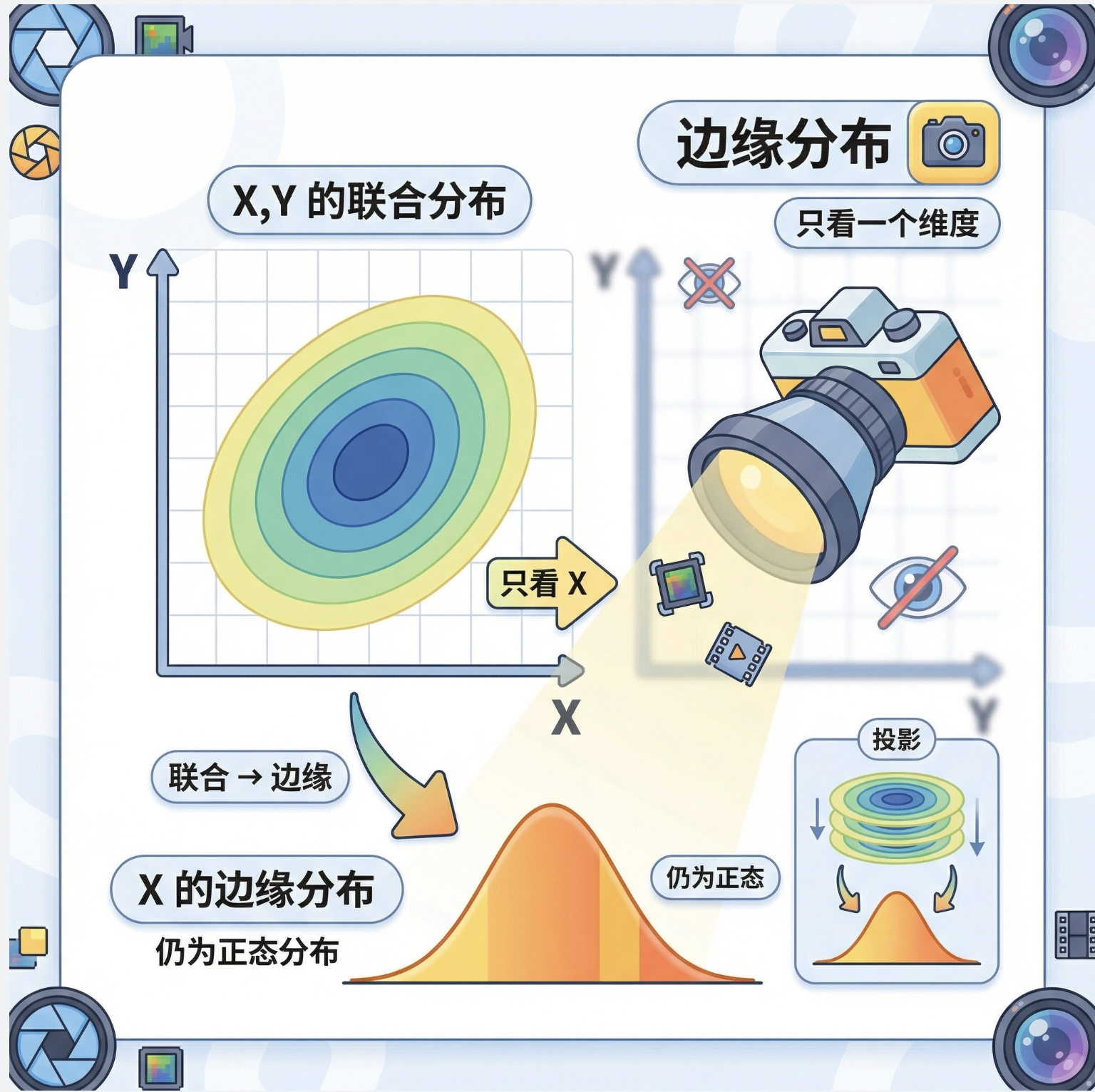
核心概念

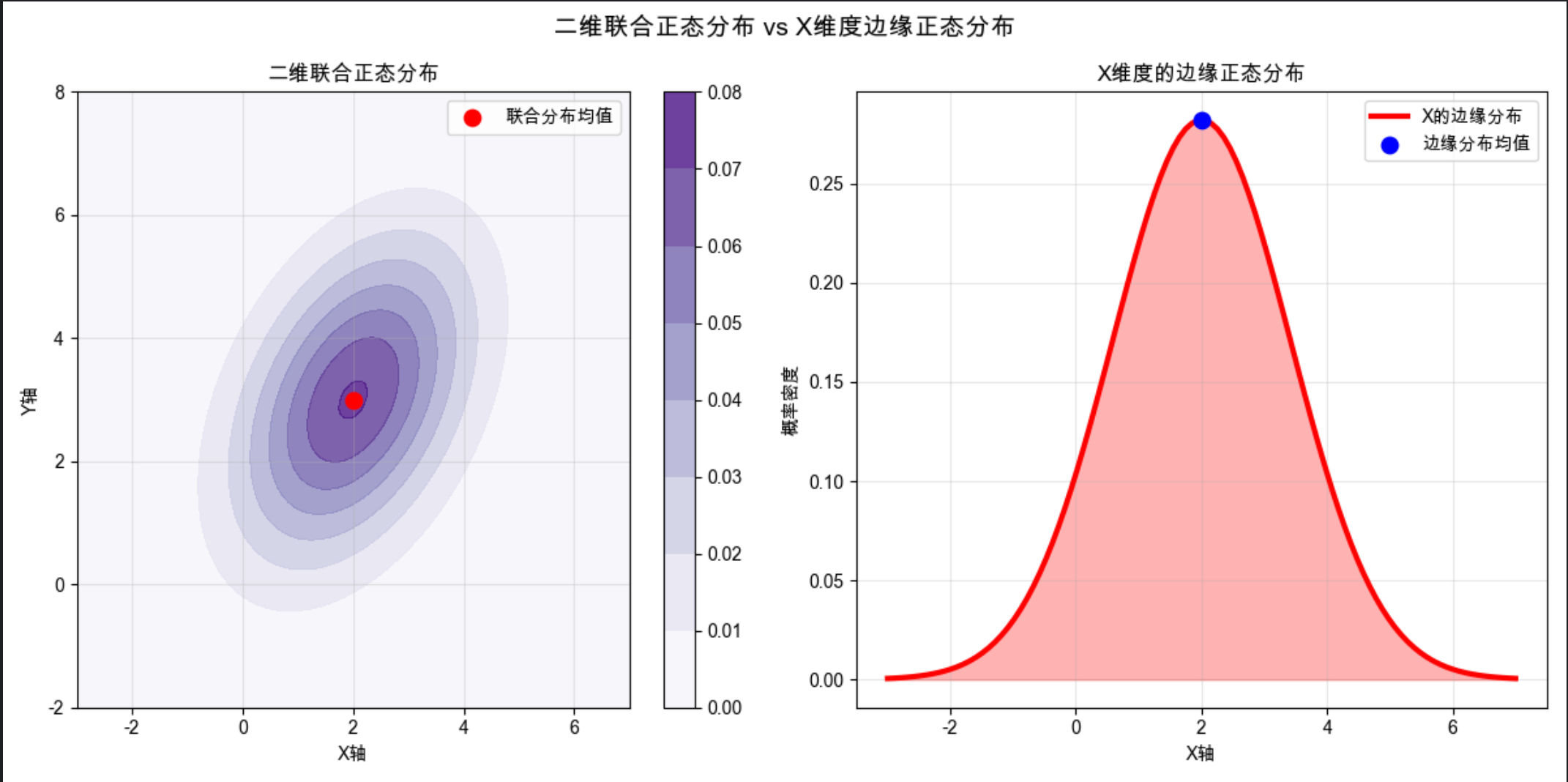
边缘分布就像 "只看分布的某一个维度"：

比如二维正态分布 (X,Y)，只看 X 的分布（忽略 Y），就是 X 的边缘分布
核心结论：多元正态分布的边缘分布依然是正态分布

完整代码 + 可视化对比

python 复制代码

# 导入所有必要的库
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal

# ==================== Mac系统Matplotlib中文显示配置 ====================
# 解决Mac系统中文显示和负号显示问题，确保图表标题/标签的中文正常显示
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']  # Mac原生支持的中文字体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示为方块的问题
plt.rcParams['font.family'] = 'Arial Unicode MS'  # 强制指定中文字体
plt.rcParams['axes.facecolor'] = 'white'  # 设置画布背景色为白色，提升显示效果

# ==================== 5.4 边缘分布 ====================
def marginal_distribution():
    """
    演示多元正态分布的边缘分布：从二维联合分布提取一维边缘分布
    - 核心结论：多元正态分布的边缘分布依然是正态分布
    - 本例提取X维度的边缘分布（忽略Y维度）
    """
    # 1. 定义二维正态分布参数（确保协方差矩阵正定）
    mean = [2, 3]  # 二维均值 [μ_x, μ_y]
    cov = [[2, 1], [1, 3]]  # 二维协方差矩阵
    # 验证正定：行列式=2*3 - 1*1 = 5 > 0，严格正定，可安全使用
    det = np.linalg.det(cov)
    print(f"二维协方差矩阵行列式：{det:.2f}（>0，正定）")
    
    # 2. 生成绘图用的网格点和数据
    x = np.linspace(-3, 7, 100)  # X轴范围
    y = np.linspace(-2, 8, 100)  # Y轴范围
    X, Y = np.meshgrid(x, y)     # 生成二维网格
    pos = np.dstack((X, Y))      # 形状(100,100,2)，对应每个网格点的坐标
    
    # 3. 计算二维联合分布的概率密度（PDF）
    rv_joint = multivariate_normal(mean, cov)
    pdf_joint = rv_joint.pdf(pos)
    
    # 4. 计算X维度的边缘分布（核心：仅取X维度的均值和方差）
    mean_x = mean[0]                # X维度的均值 = 原联合分布X维度的均值
    cov_x = cov[0][0]               # X维度的方差 = 原协方差矩阵X维度的对角线元素
    rv_marginal_x = multivariate_normal(mean_x, cov_x)  # 一维边缘正态分布
    pdf_marginal_x = rv_marginal_x.pdf(x)               # 边缘分布的PDF
    
    # 5. 可视化：联合分布 vs 边缘分布
    fig = plt.figure(figsize=(12, 6))
    
    # 子图1：二维联合正态分布（紫色等高线）
    ax1 = fig.add_subplot(121)
    contour = ax1.contourf(X, Y, pdf_joint, cmap='Purples', alpha=0.8)
    # 标记联合分布的均值点（红色实心圆）
    ax1.scatter(mean[0], mean[1], color='red', s=80, label='联合分布均值', zorder=5)
    ax1.set_title('二维联合正态分布', fontsize=12)
    ax1.set_xlabel('X轴')
    ax1.set_ylabel('Y轴')
    ax1.legend(loc='upper right')
    ax1.grid(alpha=0.3)
    plt.colorbar(contour, ax=ax1)  # 添加颜色条
    
    # 子图2：X维度的一维边缘正态分布
    ax2 = fig.add_subplot(122)
    # 绘制边缘分布曲线（红色粗线）
    ax2.plot(x, pdf_marginal_x, color='red', linewidth=3, label='X的边缘分布')
    # 填充曲线下方区域，增强视觉效果
    ax2.fill_between(x, pdf_marginal_x, alpha=0.3, color='red')
    # 标记边缘分布的均值点（蓝色实心圆）
    ax2.scatter(mean_x, rv_marginal_x.pdf(mean_x), color='blue', s=80, label='边缘分布均值', zorder=5)
    ax2.set_title('X维度的边缘正态分布', fontsize=12)
    ax2.set_xlabel('X轴')
    ax2.set_ylabel('概率密度')
    ax2.legend(loc='upper right')
    ax2.grid(alpha=0.3)
    
    # 打印边缘分布参数（辅助理解）
    print("="*50)
    print("边缘分布关键参数：")
    print(f"联合分布均值（X,Y）：{mean}")
    print(f"X维度边缘分布均值：{mean_x}")
    print(f"X维度边缘分布方差：{cov_x}")
    print("="*50)
    
    # 总标题和布局调整
    plt.suptitle('二维联合正态分布 vs X维度边缘正态分布', fontsize=14)
    plt.tight_layout()
    plt.show()

# 主程序入口：调用函数执行
if __name__ == "__main__":
    marginal_distribution()

代码解释

边缘分布的均值就是原分布对应维度的均值，方差就是原协方差矩阵对应对角线元素
左侧是二维联合分布，右侧是 X 维度的一维边缘分布，能直观看到边缘分布的 "来源"

5.5 条件分布

核心概念

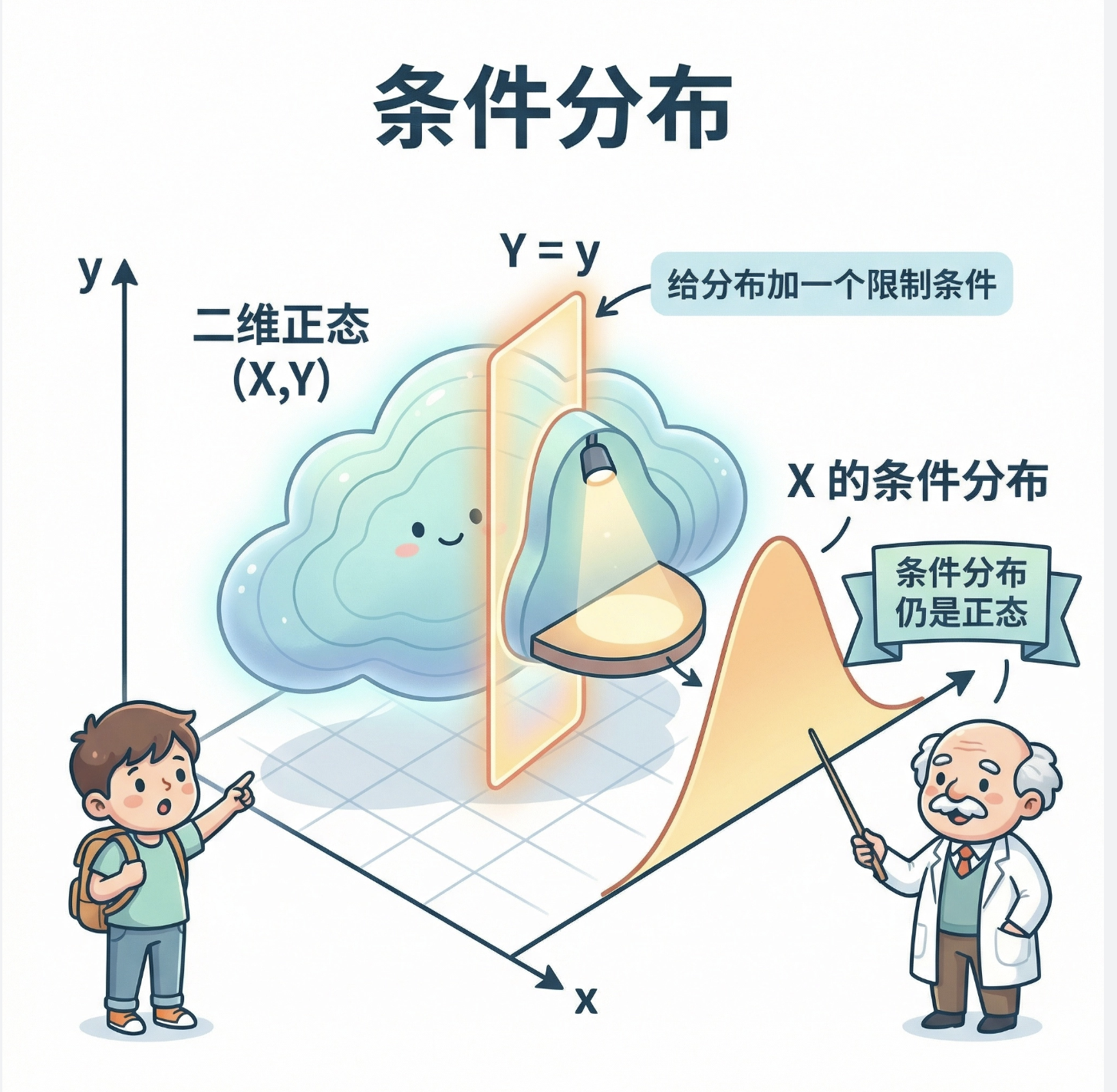
条件分布就像 "给分布加一个限制条件"：

比如二维正态分布 (X,Y)，给定 Y=y 时，X 的分布就是条件分布
核心结论：多元正态分布的条件分布依然是正态分布

完整代码 + 可视化

python 复制代码

# 导入所有必要的库
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal

# ==================== Mac系统Matplotlib中文显示配置 ====================
# 解决Mac系统中文显示和负号显示问题，确保图表标题/标签的中文正常显示
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']  # Mac原生支持的中文字体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示为方块的问题
plt.rcParams['font.family'] = 'Arial Unicode MS'  # 强制指定中文字体
plt.rcParams['axes.facecolor'] = 'white'  # 设置画布背景色为白色，提升显示效果

# ==================== 5.5 条件分布 ====================
def conditional_distribution():
    """
    演示二维正态分布的条件分布：给定Y=y时，X的条件分布
    - 核心结论：多元正态分布的条件分布依然是正态分布
    - 核心公式：
      条件均值：μ₁|₂ = μ₁ + σ₁₂/σ₂₂*(y - μ₂)
      条件方差：σ₁|₂ = σ₁₁ - σ₁₂/σ₂₂*σ₂₁
    """
    # 1. 定义二维正态分布参数（验证正定）
    mean = [0, 0]  # 二维均值 [μ₁, μ₂]
    cov = [[4, 2], [2, 3]]  # 二维协方差矩阵
    # 验证正定：行列式=4*3 - 2*2 = 8 > 0，严格正定
    det = np.linalg.det(cov)
    print(f"二维协方差矩阵行列式：{det:.2f}（>0，正定）")
    
    # 2. 拆分协方差矩阵参数（便于计算条件分布）
    mu1, mu2 = mean[0], mean[1]          # 两个维度的均值
    sigma11, sigma12 = cov[0][0], cov[0][1]  # σ₁₁=X方差，σ₁₂=X-Y协方差
    sigma21, sigma22 = cov[1][0], cov[1][1]  # σ₂₁=Y-X协方差，σ₂₂=Y方差
    
    # 3. 定义条件值并计算条件分布参数
    y_given = 2  # 给定Y=2（条件）
    # 计算条件分布的均值（核心公式）
    mu_conditional = mu1 + sigma12 * (1/sigma22) * (y_given - mu2)
    # 计算条件分布的方差（核心公式）
    sigma_conditional = sigma11 - sigma12 * (1/sigma22) * sigma21
    
    # 4. 生成绘图用的数据
    x = np.linspace(-8, 8, 100)  # X轴范围
    y = np.linspace(-8, 8, 100)  # Y轴范围
    X, Y = np.meshgrid(x, y)     # 二维网格点
    pos = np.dstack((X, Y))      # 形状(100,100,2)的坐标数组
    
    # 5. 计算联合分布和条件分布的PDF
    rv_joint = multivariate_normal(mean, cov)  # 二维联合分布
    pdf_joint = rv_joint.pdf(pos)              # 联合分布PDF
    rv_conditional = multivariate_normal(mu_conditional, sigma_conditional)  # 条件分布
    pdf_conditional = rv_conditional.pdf(x)    # 条件分布PDF
    
    # 6. 可视化：联合分布 + 条件线 + 条件分布
    fig = plt.figure(figsize=(12, 6))
    
    # 子图1：二维联合分布 + 条件线（Y=2）
    ax1 = fig.add_subplot(121)
    contour = ax1.contourf(X, Y, pdf_joint, cmap='Greens', alpha=0.8)
    # 绘制条件线（Y=2，红色虚线，突出条件约束）
    ax1.axhline(y=y_given, color='red', linestyle='--', linewidth=3, label=f'Y={y_given}（条件）')
    # 标记联合分布均值点（蓝色实心圆）
    ax1.scatter(mu1, mu2, color='blue', s=80, label='联合分布均值', zorder=5)
    ax1.set_title('二维联合正态分布 + 条件线', fontsize=12)
    ax1.set_xlabel('X轴')
    ax1.set_ylabel('Y轴')
    ax1.legend(loc='upper right')
    ax1.grid(alpha=0.3)
    plt.colorbar(contour, ax=ax1)  # 添加颜色条
    
    # 子图2：给定Y=2时X的条件分布
    ax2 = fig.add_subplot(122)
    # 绘制条件分布曲线（蓝色粗线）
    ax2.plot(x, pdf_conditional, color='blue', linewidth=3, label=f'Y={y_given}时X的条件分布')
    # 填充曲线下方区域，增强视觉效果
    ax2.fill_between(x, pdf_conditional, alpha=0.3, color='blue')
    # 标记条件分布的均值点（红色实心圆）
    ax2.scatter(mu_conditional, rv_conditional.pdf(mu_conditional), color='red', s=80, label='条件分布均值', zorder=5)
    # 绘制条件均值的竖线（辅助观察）
    ax2.axvline(x=mu_conditional, color='orange', linestyle='--', linewidth=2, label='条件均值')
    ax2.set_title(f'给定Y={y_given}时X的条件正态分布', fontsize=12)
    ax2.set_xlabel('X轴')
    ax2.set_ylabel('概率密度')
    ax2.legend(loc='upper right')
    ax2.grid(alpha=0.3)
    
    # 打印条件分布参数（辅助理解）
    print("="*50)
    print("条件分布关键参数：")
    print(f"给定条件：Y = {y_given}")
    print(f"条件分布均值（μ₁|₂）：{np.round(mu_conditional, 3)}")
    print(f"条件分布方差（σ₁|₂）：{np.round(sigma_conditional, 3)}")
    print("="*50)
    
    # 总标题和布局调整
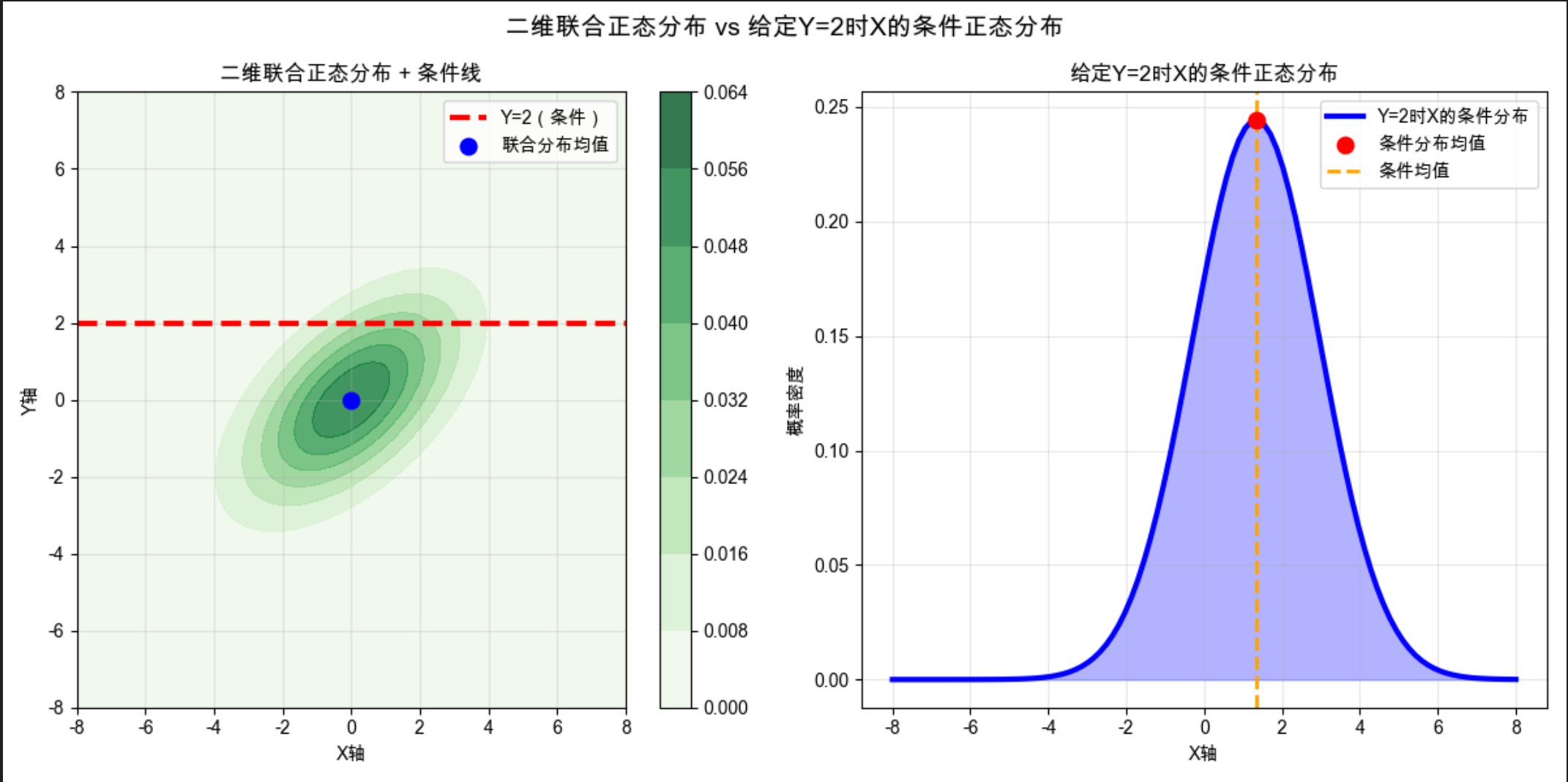
    plt.suptitle('二维联合正态分布 vs 给定Y=2时X的条件正态分布', fontsize=14)
    plt.tight_layout()
    plt.show()

# 主程序入口：调用函数执行
if __name__ == "__main__":
    conditional_distribution()

代码解释

条件分布的均值和方差计算公式已简化为直观的形式，避免复杂推导
红色虚线是 "条件线（Y=2）"，右侧是此时 X 的条件分布，能清晰看到条件分布的 "约束性"

5.6 正态分布的乘积

核心概念

正态分布的乘积就像 "两个分布的融合"：

核心结论：两个正态分布的乘积依然是正态分布（需归一化）
应用场景：贝叶斯推断中 "先验 × 似然 = 后验"

完整代码 + 可视化对比

python 复制代码

# 导入所有必要的库
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal

# ==================== Mac系统Matplotlib中文显示配置 ====================
# 解决Mac系统中文显示和负号显示问题，确保图表标题/标签的中文正常显示
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']  # Mac原生支持的中文字体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示为方块的问题
plt.rcParams['font.family'] = 'Arial Unicode MS'  # 强制指定中文字体
plt.rcParams['axes.facecolor'] = 'white'  # 设置画布背景色为白色，提升显示效果

# ==================== 5.6 正态分布的乘积 ====================
def normal_product():
    """
    演示两个一维正态分布的乘积运算
    - 核心结论：两个正态分布的乘积（归一化后）依然是正态分布
    - 应用场景：贝叶斯推断中"先验分布 × 似然分布 = 后验分布"
    """
    # 1. 定义两个一维正态分布的参数（均值+方差）
    mean1, sigma1 = 1, 1.5  # 分布1：N(1, 1.5)
    mean2, sigma2 = 3, 1.0  # 分布2：N(3, 1.0)
    
    # 2. 生成绘图用的X轴数据（更密集的点让曲线更平滑）
    x = np.linspace(-4, 8, 200)  # 范围覆盖两个分布的主要区域
    
    # 3. 计算两个正态分布的概率密度（PDF）
    rv1 = multivariate_normal(mean1, sigma1)  # 分布1对象
    rv2 = multivariate_normal(mean2, sigma2)  # 分布2对象
    pdf1 = rv1.pdf(x)  # 分布1的PDF值
    pdf2 = rv2.pdf(x)  # 分布2的PDF值
    
    # 4. 计算两个分布的乘积并归一化
    # 原始乘积：仅数学运算，未满足PDF的"积分和为1"要求
    product_raw = pdf1 * pdf2
    # 归一化：除以最大值，使乘积结果的峰值为1（便于可视化对比）
    product_normalized = product_raw / np.max(product_raw)
    
    # 5. 可视化：两个原始分布 + 乘积分布
    plt.figure(figsize=(10, 6))
    
    # 绘制原始分布1（蓝色实线）
    plt.plot(x, pdf1, label=f'分布1: N(μ={mean1}, σ²={sigma1})', 
             color='blue', linewidth=3, alpha=0.8)
    # 绘制原始分布2（绿色实线）
    plt.plot(x, pdf2, label=f'分布2: N(μ={mean2}, σ²={sigma2})', 
             color='green', linewidth=3, alpha=0.8)
    # 绘制乘积分布（红色虚线）
    plt.plot(x, product_normalized, label='分布1 × 分布2（归一化）', 
             color='red', linewidth=3, linestyle='--', alpha=0.8)
    
    # 填充曲线下方区域，增强视觉对比
    plt.fill_between(x, pdf1, alpha=0.2, color='blue')
    plt.fill_between(x, pdf2, alpha=0.2, color='green')
    plt.fill_between(x, product_normalized, alpha=0.3, color='red')
    
    # 标记两个原始分布的均值点（实心圆）
    plt.scatter(mean1, rv1.pdf(mean1), color='blue', s=100, zorder=5, label='分布1均值')
    plt.scatter(mean2, rv2.pdf(mean2), color='green', s=100, zorder=5, label='分布2均值')
    # 标记乘积分布的峰值点（红色五角星）
    peak_idx = np.argmax(product_normalized)
    plt.scatter(x[peak_idx], product_normalized[peak_idx], color='red', marker='*', s=200, zorder=6, label='乘积分布峰值')
    
    # 图表样式配置
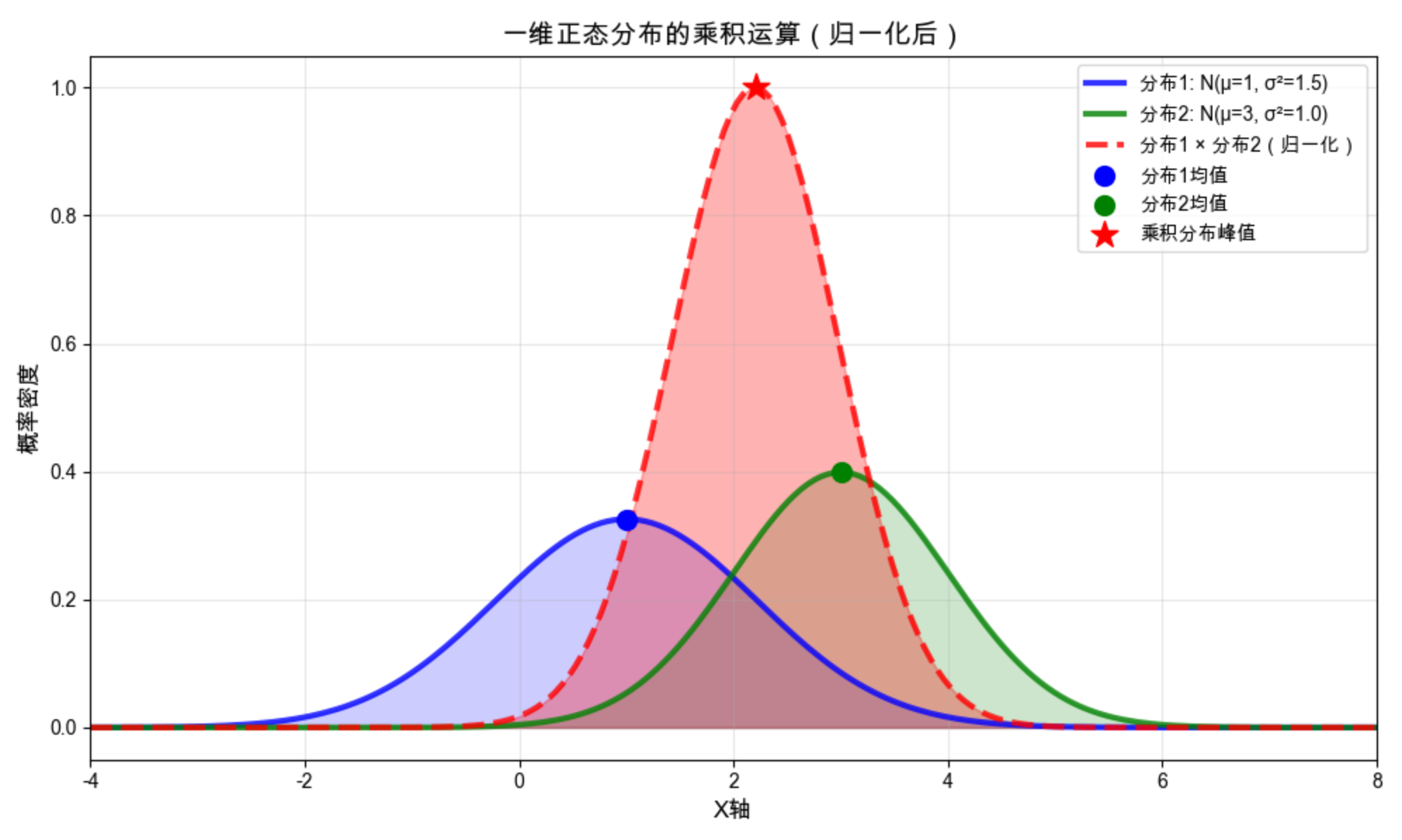
    plt.title('一维正态分布的乘积运算（归一化后）', fontsize=14)
    plt.xlabel('X轴', fontsize=12)
    plt.ylabel('概率密度', fontsize=12)
    plt.legend(loc='upper right', fontsize=10)
    plt.grid(alpha=0.3)  # 浅灰色网格，提升可读性
    plt.xlim(-4, 8)      # 固定X轴范围，避免自动缩放
    
    # 打印关键信息（辅助理解）
    print("="*50)
    print("正态分布乘积关键信息：")
    print(f"分布1：均值={mean1}，方差={sigma1}")
    print(f"分布2：均值={mean2}，方差={sigma2}")
    print(f"乘积分布峰值位置：X={x[peak_idx]:.2f}")
    print("核心结论：两个正态分布的乘积（归一化后）仍为正态分布")
    print("="*50)
    
    plt.tight_layout()
    plt.show()

# 主程序入口：调用函数执行
if __name__ == "__main__":
    normal_product()

代码解释

红色虚线是两个分布的乘积（归一化后），能看到乘积分布是 "融合了两个分布特征" 的新正态分布

归一化是为了让乘积结果符合概率密度的定义（积分和为 1）

5.7 变量改变

核心概念

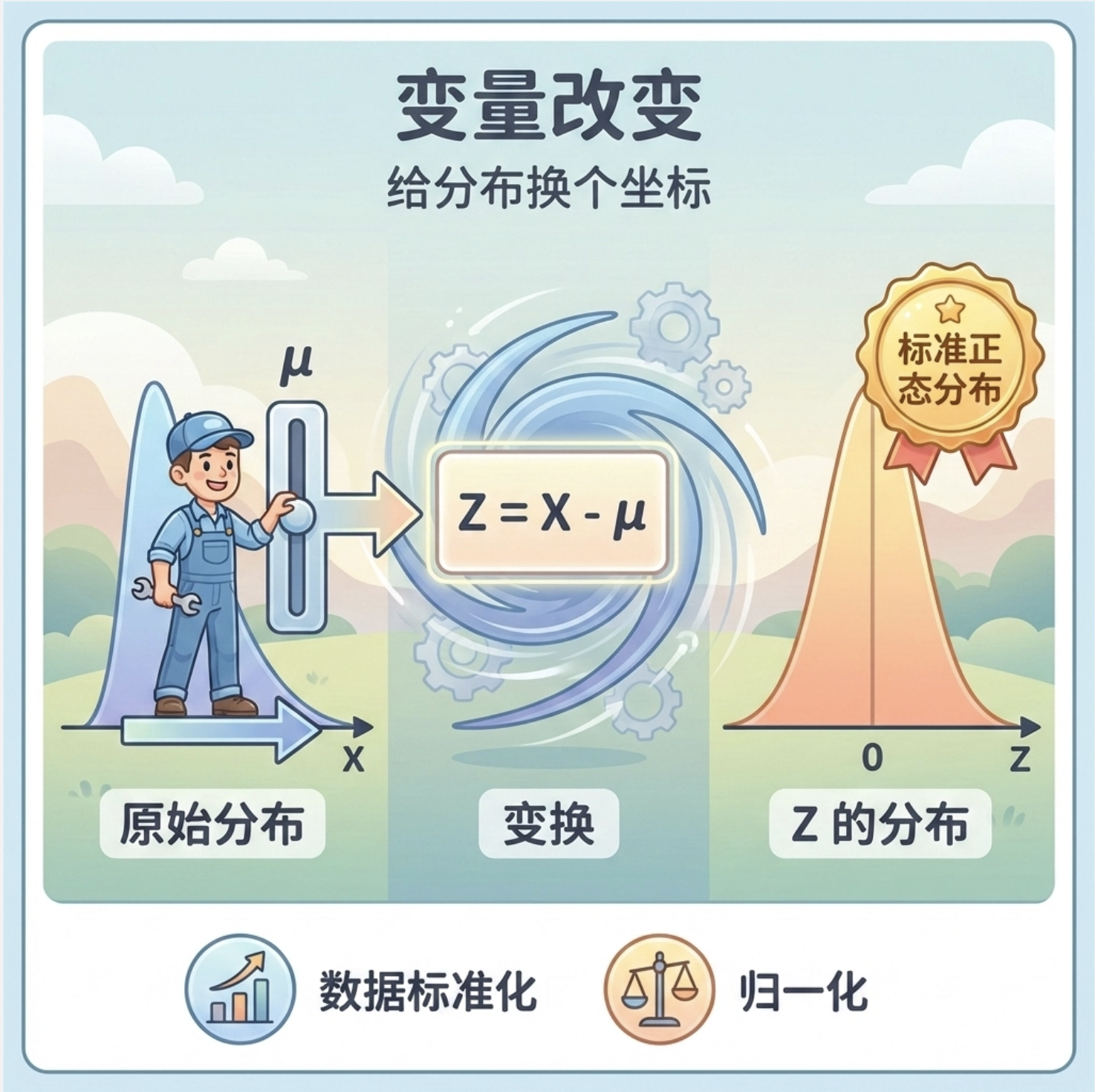
变量改变就像 "给分布换个坐标"：

核心操作：通过变量替换（如 Z = X - μ），将原分布转换为标准正态分布
应用场景：数据标准化、归一化

完整代码 + 可视化

python 复制代码

# 导入所有必要的库
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal

# ==================== Mac系统Matplotlib中文显示配置 ====================
# 解决Mac系统中文显示和负号显示问题，确保图表标题/标签的中文正常显示
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']  # Mac原生支持的中文字体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示为方块的问题
plt.rcParams['font.family'] = 'Arial Unicode MS'  # 强制指定中文字体
plt.rcParams['axes.facecolor'] = 'white'  # 设置画布背景色为白色，提升显示效果

# ==================== 5.7 变量改变 ====================
def variable_change():
    """
    演示正态分布的变量改变：中心化 → 标准化
    - 中心化：Z = X - μ（仅平移，分布形状不变，均值变为0）
    - 标准化：Z = (X - μ)/σ（平移+缩放，均值=0，方差=1，变为标准正态分布）
    - 核心结论：变量线性变换后，正态分布的形态仅发生平移/缩放，仍为正态分布
    """
    # 1. 定义原始非标准正态分布参数（验证正定）
    mean_original = [2, 3]  # 原始均值 [μ₁, μ₂]
    cov_original = [[2, 0.5], [0.5, 1.5]]  # 原始协方差矩阵
    # 验证正定：行列式=2*1.5 - 0.5*0.5 = 2.75 > 0，严格正定
    det = np.linalg.det(cov_original)
    print(f"原始协方差矩阵行列式：{det:.2f}（>0，正定）")
    
    # 2. 变量改变1：中心化（Z = X - μ）
    mean_centered = [0, 0]  # 中心化后均值为0
    cov_centered = cov_original  # 中心化不改变协方差矩阵（仅平移，形状不变）
    
    # 3. 变量改变2：标准化（Z = (X - μ)/σ，完整线性变换）
    # 计算各维度的标准差（协方差矩阵对角线元素开平方）
    stds = np.sqrt(np.diag(cov_original))  # [√2, √1.5] ≈ [1.414, 1.225]
    # 构建标准化变换矩阵A = diag(1/σ₁, 1/σ₂)
    A_standard = np.diag(1 / stds)
    # 标准化后的均值：A·(μ_original - μ_original) = [0,0]
    mean_standard = [0, 0]
    # 标准化后的协方差：A·cov_original·Aᵀ = 单位矩阵（标准正态分布）
    cov_standard = A_standard @ cov_original @ A_standard.T
    
    # 4. 生成绘图用的网格点（覆盖足够范围，展示所有分布）
    x = np.linspace(-6, 10, 100)
    y = np.linspace(-4, 10, 100)
    X, Y = np.meshgrid(x, y)
    pos = np.dstack((X, Y))  # 形状(100,100,2)的坐标数组
    
    # 5. 计算三个分布的概率密度（PDF）
    # 原始分布
    rv_original = multivariate_normal(mean_original, cov_original)
    pdf_original = rv_original.pdf(pos)
    # 中心化分布
    rv_centered = multivariate_normal(mean_centered, cov_centered)
    pdf_centered = rv_centered.pdf(pos)
    # 标准化分布
    rv_standard = multivariate_normal(mean_standard, cov_standard)
    pdf_standard = rv_standard.pdf(pos)
    
    # 6. 可视化：原始分布 → 中心化 → 标准化（3个子图对比）
    fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(15, 5))
    
    # 子图1：原始正态分布
    contour1 = ax1.contourf(X, Y, pdf_original, cmap='Blues', alpha=0.8)
    # 标记原始均值点（红色实心圆）
    ax1.scatter(mean_original[0], mean_original[1], color='red', s=100, label='原始均值', zorder=5)
    ax1.set_title('原始正态分布', fontsize=12)
    ax1.set_xlabel('X轴')
    ax1.set_ylabel('Y轴')
    ax1.legend(loc='upper right')
    ax1.grid(alpha=0.3)
    fig.colorbar(contour1, ax=ax1)
    
    # 子图2：中心化分布（Z = X - μ）
    contour2 = ax2.contourf(X, Y, pdf_centered, cmap='Greens', alpha=0.8)
    # 标记中心化后的均值点（红色实心圆，原点）
    ax2.scatter(mean_centered[0], mean_centered[1], color='red', s=100, label='中心化均值(0,0)', zorder=5)
    ax2.set_title('中心化分布（Z=X-μ）', fontsize=12)
    ax2.set_xlabel('X轴')
    ax2.set_ylabel('Y轴')
    ax2.legend(loc='upper right')
    ax2.grid(alpha=0.3)
    fig.colorbar(contour2, ax=ax2)
    
    # 子图3：标准正态分布（Z=(X-μ)/σ）
    contour3 = ax3.contourf(X, Y, pdf_standard, cmap='Reds', alpha=0.8)
    # 标记标准化后的均值点（红色实心圆，原点）
    ax3.scatter(mean_standard[0], mean_standard[1], color='red', s=100, label='标准化均值(0,0)', zorder=5)
    ax3.set_title('标准正态分布（Z=(X-μ)/σ）', fontsize=12)
    ax3.set_xlabel('X轴')
    ax3.set_ylabel('Y轴')
    ax3.legend(loc='upper right')
    ax3.grid(alpha=0.3)
    fig.colorbar(contour3, ax=ax3)
    
    # 打印关键参数（辅助理解变量改变的效果）
    print("="*50)
    print("变量改变关键参数：")
    print(f"原始均值：{mean_original}")
    print(f"中心化均值：{mean_centered}")
    print(f"标准化均值：{mean_standard}")
    print(f"原始协方差矩阵：\n{np.round(cov_original, 3)}")
    print(f"中心化协方差矩阵：\n{np.round(cov_centered, 3)}")
    print(f"标准化协方差矩阵（单位矩阵）：\n{np.round(cov_standard, 3)}")
    print("="*50)
    
    # 总标题和布局调整
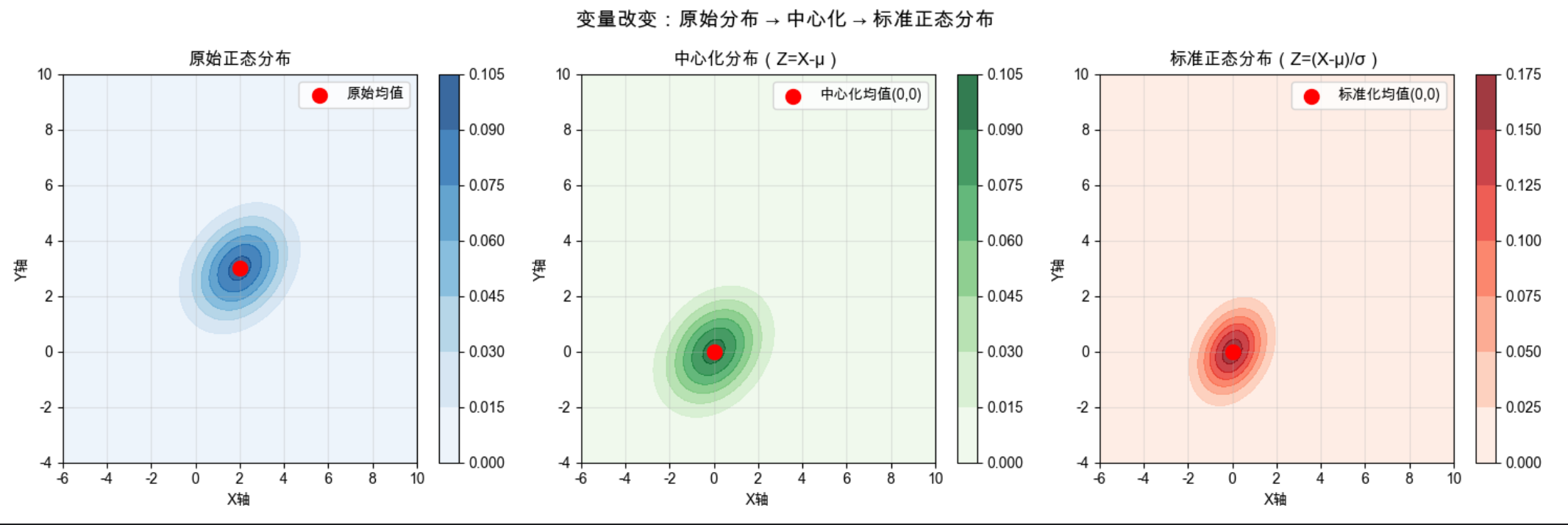
    plt.suptitle('变量改变：原始分布 → 中心化 → 标准正态分布', fontsize=14)
    plt.tight_layout()
    plt.show()

# 主程序入口：调用函数执行
if __name__ == "__main__":
    variable_change()

代码解释

中心化：将分布的均值移到原点（不改变形状）
标准化：不仅中心化，还将各维度方差变为 1（变成 "标准圆"）
三个子图能清晰看到变量改变的 "递进效果"

总结

核心要点

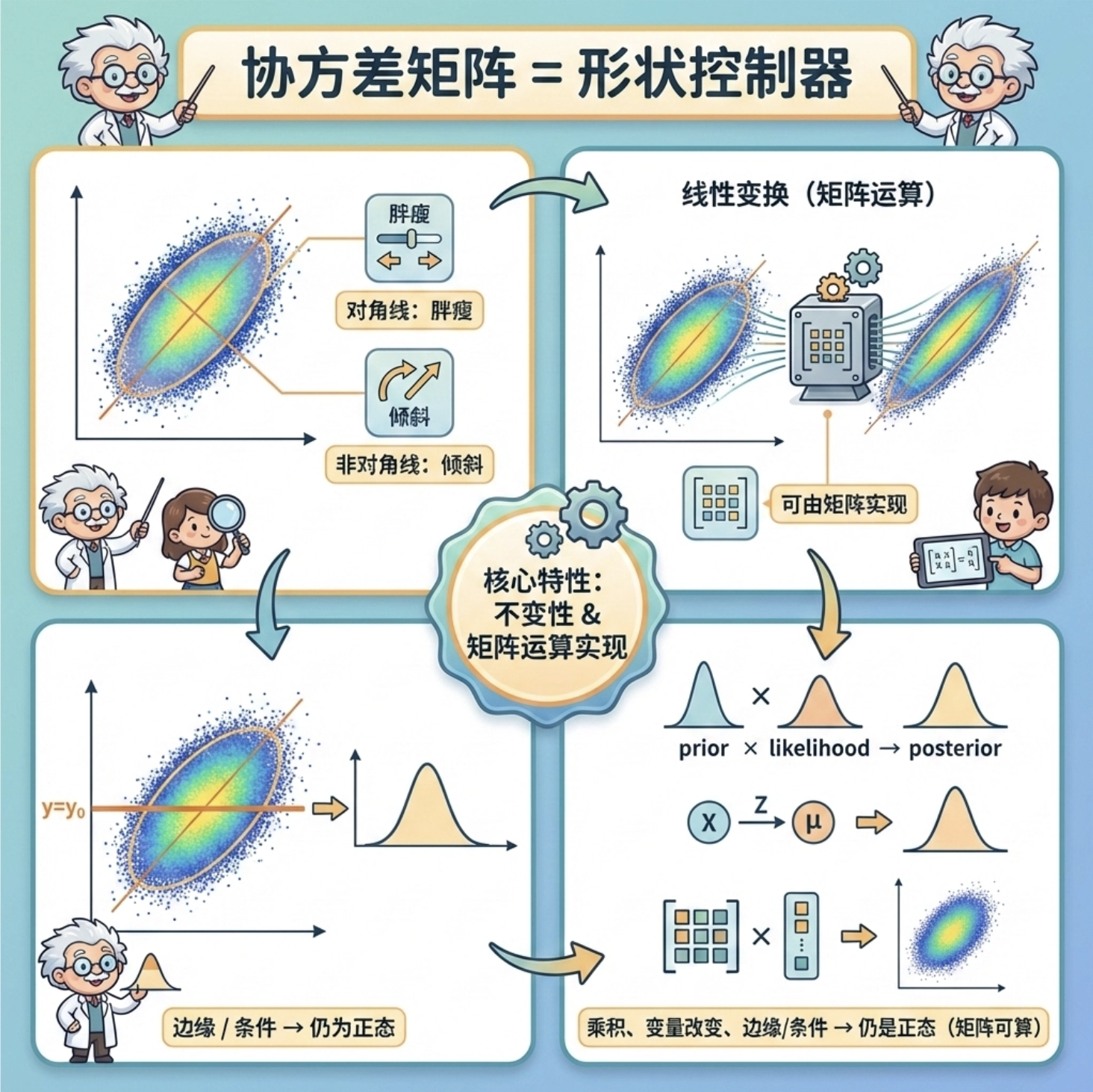
1.协方差矩阵是正态分布的 "形状控制器"，对角线控制胖瘦，非对角线控制倾斜；

2.正态分布经过线性变换、边缘 / 条件操作、乘积、变量改变后，依然是正态分布（核心特性）；

3.所有操作都可通过简单的矩阵运算实现，可视化是理解分布变化的最佳方式。

备注

1.本文所有代码均基于 Mac 系统编写，Windows/Linux 用户只需修改 Matplotlib 中文配置即可运行；

2.代码中避免了复杂公式，核心逻辑用通俗语言 + 可视化替代，便于新手理解；

3.正态分布是计算机视觉的基础，建议动手运行代码，修改参数（如协方差矩阵、变换矩阵）观察分布变化。

习题

1.修改 5.1 中的协方差矩阵，将非对角线元素改为 - 1.5，观察分布的倾斜方向变化；

2.基于 5.3 的线性变换代码，尝试仅旋转（A 为旋转矩阵）、仅缩放（A 为对角矩阵），观察分布变化；

3.基于 5.6 的乘积代码，尝试两个均值相同、方差不同的分布，观察乘积结果的特征。

最后

希望这篇文章能帮你吃透《计算机视觉：模型、学习和推理》第 5 章的正态分布知识点！所有代码都可直接运行，建议动手实操，加深理解。如果有问题，欢迎在评论区交流～