深度范式转移：漂移模型（Drifting Models）解析

论文：Generative Modeling via Drifting

引言

在当前的生成式人工智能领域，扩散模型（Diffusion Models）和流匹配（Flow Matching）占据了主导地位。这些模型的核心逻辑是通过在推理阶段（Inference-time）求解常微分方程（ODE）或随机微分方程（SDE）来实现从先验分布到数据分布的映射。然而，这类方法依赖于多步迭代网络调用（NFE > 1），在计算效率上存在天然瓶颈。

何恺明近期提出的 Drifting Models（漂移模型） 提出了一种截然不同的范式：将样本分布的演进从"推理阶段"转移至"训练阶段"。通过引入一种基于吸引与排斥机制的漂移场（Drifting Field），模型能够在单次前向传播中完成生成。

1. 核心机制：训练时分布演进

Drifting Models 的核心目标是学习一个单步映射函数 fθf_\thetafθ，使得先验分布 pϵp_\epsilonpϵ 的推前分布（Pushforward Distribution）q=f#(ϵ)q = f_{\#}(\epsilon)q=f#(ϵ) 能够匹配目标数据分布 pdatap_{data}pdata。

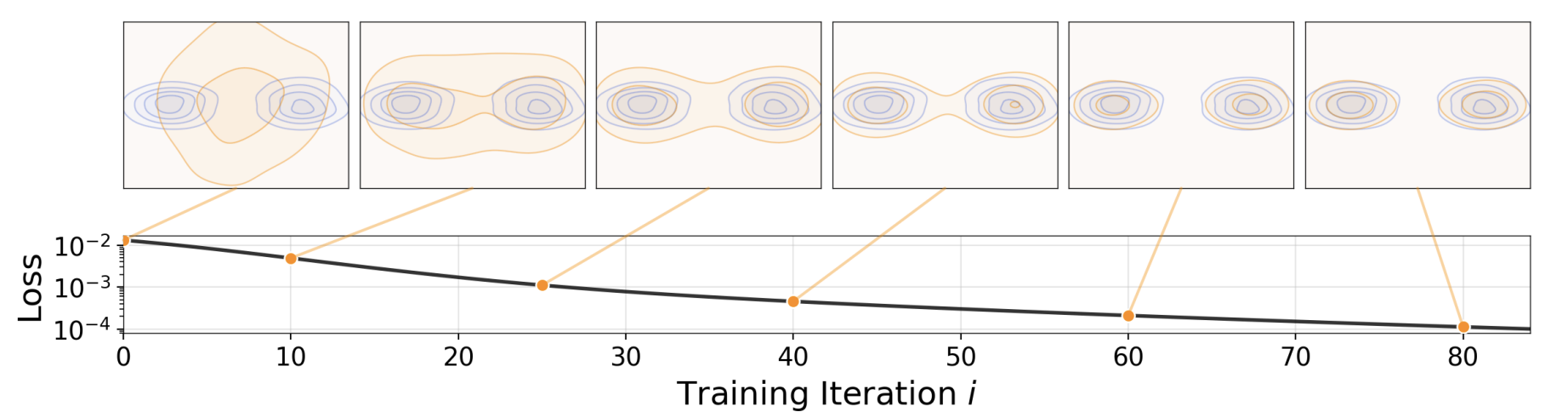
图1 漂移模型 ：网络fff执行前推操作：q=f#ppriorq=f_{\#} p_{\text{prior}}q=f#pprior，将先验分布ppriorp_{\text{prior}}pprior（如高斯分布，图中未展示）映射为前推分布qqq（橙色）。训练的目标是让该分布逼近数据分布pdatap_{\text{data}}pdata（蓝色）。随着训练迭代进行，我们得到一系列模型{fi}\{f_i\}{fi}，对应一系列前推分布{qi}\{q_i\}{qi}。本文的漂移模型聚焦于训练阶段前推分布的演化过程。论文引入了一个漂移场，当分布qqq与数据分布pdatap_{\text{data}}pdata匹配时，该漂移场趋于零。
pushforward operation/ distribution：前推操作/前推分布（概率论专业术语，指通过映射将一个分布转化为另一个分布，也译作"推送操作/分布"）

与扩散模型通过预设的噪声调度（Noise Schedule）定义演进路径不同，Drifting Models 利用训练迭代过程中的自然演化。在第 iii 次训练迭代时，模型 fif_ifi 对应一个推前分布 qiq_iqi。研究者引入漂移场 Vp,q\mathbf{V}{p,q}Vp,q 指导分布的移动：
xi+1=xi+Vp,q(xi)\mathbf{x}{i+1} = \mathbf{x}i + \mathbf{V}{p,q}(\mathbf{x}_i)xi+1=xi+Vp,q(xi)

当 q=pq = pq=p 时，漂移场达到平衡状态（V=0\mathbf{V} = 0V=0）。

2. 漂移场（Drifting Field）的数学构建

漂移场的构造灵感来源于经典统计学中的均值漂移（Mean-shift）算法。为了确保收敛性与稳定性，漂移场被定义为正向引力与负向斥力的线性叠加：
Vp,q(x)=Vp+(x)−Vq−(x)\mathbf{V}_{p,q}(\mathbf{x}) = \mathbf{V}^+_p(\mathbf{x}) - \mathbf{V}^-_q(\mathbf{x})Vp,q(x)=Vp+(x)−Vq−(x)

其中，Vp+\mathbf{V}^+_pVp+ 由数据分布 ppp 提供吸引力，Vq−\mathbf{V}^-qVq− 由生成分布 qqq 提供排斥力。通过核函数 k(x,y)k(\mathbf{x}, \mathbf{y})k(x,y) 衡量样本间的相似性，其具体形式为（y+\textbf{y}^{+}y+来自数据分布，x\textbf{x}x来自生成分布）：
Vp+(x)=1Ey+∼p[k(x,y+)]Ey+∼p[k(x,y+)(y+−x)]\mathbf{V}^+p(\mathbf{x}) = \frac{1}{\mathbb{E}{\mathbf{y}^+ \sim p} [k(\mathbf{x}, \mathbf{y}^+)]} \mathbb{E}{\mathbf{y}^+ \sim p} [k(\mathbf{x}, \mathbf{y}^+)(\mathbf{y}^+ - \mathbf{x})]Vp+(x)=Ey+∼p[k(x,y+)]1Ey+∼p[k(x,y+)(y+−x)]

这种反对称（Anti-symmetric）的构造确保了当生成分布与数据分布重合时，样本受到的总作用力为零，从而维持分布的平衡。

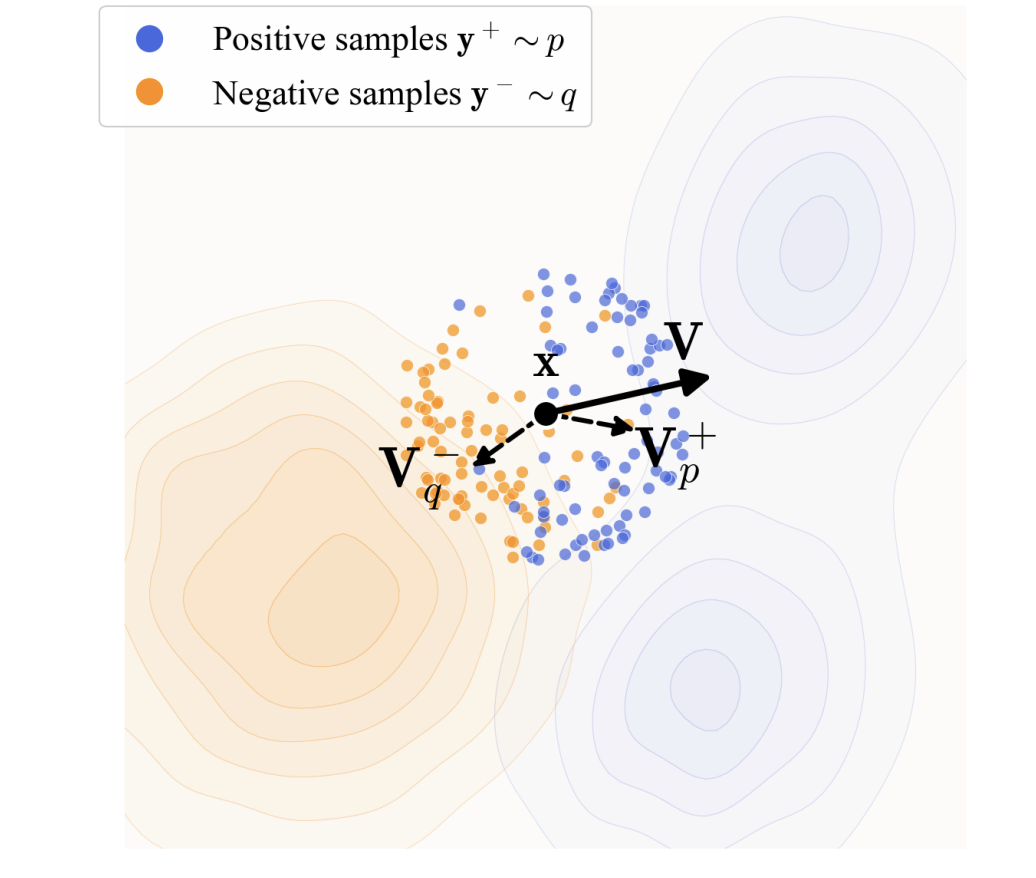
图2 样本漂移示意图 ：生成样本xxx（黑色）沿向量V=Vp+−Vq−V=V_{p}^{+}-V_{q}^{-}V=Vp+−Vq−产生漂移。其中Vp+V_{p}^{+}Vp+为正样本（蓝色）的均值漂移向量，Vq−V_{q}^{-}Vq−为负样本（橙色）的均值漂移向量。样本xxx受Vp+V_{p}^{+}Vp+的吸引作用、受Vq−V_{q}^{-}Vq−的排斥作用发生漂移。

3. 训练目标：固定点迭代与 Stop-gradient

Drifting Models 的训练目标并非直接最小化分布间距（如 KL 散度或 W 距离），而是建立一个固定点回归（Fixed-point Regression）任务。其损失函数定义如下：
L=Eϵ[∥fθ(ϵ)−sg(fθ(ϵ)+Vp,qθ(fθ(ϵ)))∥2]\mathcal{L} = \mathbb{E}\epsilon [ \| f\theta(\epsilon) - \text{sg}(f_\theta(\epsilon) + \mathbf{V}{p,q\theta}(f_\theta(\epsilon))) \|^2 ]L=Eϵ[∥fθ(ϵ)−sg(fθ(ϵ)+Vp,qθ(fθ(ϵ)))∥2]

其中 sg(⋅)\text{sg}(\cdot)sg(⋅) 表示梯度阻断（Stop-gradient）操作。

为什么使用 Stop-gradient？

这一设计与何恺明此前在 SimSiam (Simple Siamese) 中的发现具有方法论一致性。在 SimSiam 中，stop-gradient 是防止双孪生网络发生表征退化（Collapse）的核心。

SimSiam主要解决自监督对比学习的崩溃解问题（不论输入什么，特征提取器都是相同的输出），并且不同于 SimCLR、MoCo 等依赖负样本对构建对比损失的方法，SimSiam 仅通过最小化同一图像两个增强视图的负余弦相似度进行学习，全程不引入负样本，也无需大批次数据或动量编码器。

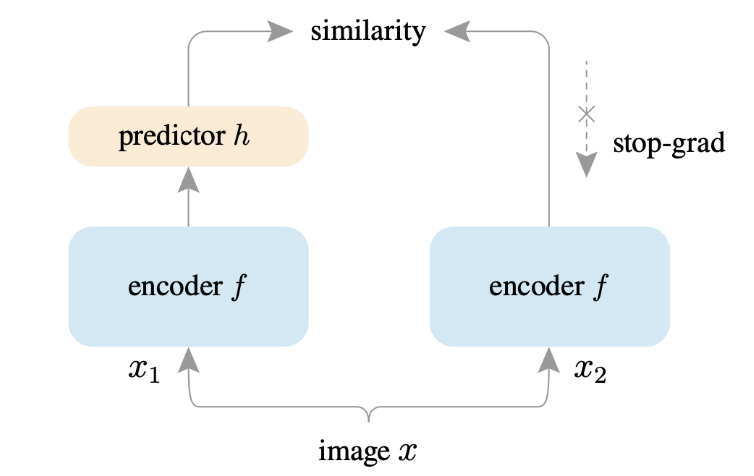
SimSiam架构：它让支路 1 去预测支路 2 的输出，但在计算梯度时，停止了支路 2 的梯度回传。
直观理解：支路 2 被当成了一个"静态的目标"。网络被迫去"追赶"这个目标，而目标本身不会为了迎合网络而主动收缩到一个常数点。这种不对称性打破了对称梯度下降导致的崩溃。

在 Drifting Models 中，stop-gradient 扮演了类似的角色：

解耦优化目标 ：它将"漂移后的位置"视为一个冻结的（Frozen）目标，避免了通过复杂的核函数计算以及通过整个分布 qqq 进行反向传播。这使得优化过程在数学上等价于一种隐式的 Expectation-Maximization (EM) 算法。
动力学稳定：通过将更新后的状态作为目标而非直接最小化漂移场本身，网络被迫学习如何直接映射到稳定流形上。

4. 特征空间漂移（Drifting in Feature Space）

实验表明，直接在像素空间计算漂移场由于维度过高和语义信息匮乏，往往难以收敛。Drifting Models 引入了特征提取器 ϕ\phiϕ （如预训练的自监督 MAE），在语义特征空间执行上述动力学过程：
Lfeat=E[∥ϕ(f(ϵ))−sg(ϕ(f(ϵ))+Vϕ)∥2]\mathcal{L}{feat} = \mathbb{E} [ \| \phi(f(\epsilon)) - \text{sg}(\phi(f(\epsilon)) + \mathbf{V}{\phi}) \|^2 ]Lfeat=E[∥ϕ(f(ϵ))−sg(ϕ(f(ϵ))+Vϕ)∥2]

这种设计使得模型能够优先捕获图像的高层结构信息。由于特征提取仅在训练时用于计算损失，而在推理时并不参与计算，因此不影响生成速度。

5. 实验分析与结论

在 ImageNet 256×256 基准测试中，Drifting Models 展现了卓越的性能：

1-NFE 性能 ：在 Latent Space 下达到 1.54 FID ，在 Pixel Space 下达到 1.61 FID。这一指标不仅超越了所有非蒸馏的一步生成模型，甚至优于许多多步迭代的扩散模型。
分类器自由引导（CFG）：该模型通过在训练阶段引入无条件样本作为负样本，实现了单步推理下的 CFG 增强效果。
泛化能力：在机器人运动规划任务（Robotics Control）中，Drifting Policy 在单步推理下的表现与需要 100 步迭代的 Diffusion Policy 相当，验证了该框架在时效性要求较高任务中的巨大潜力。

总结

Drifting Models 标志着生成模型从"推理时迭代"向"训练时演进"的范式转变。通过结合漂移场动力学与 SimSiam 式的非对称优化技巧，它解决了生成模型在质量与速度之间的长期博弈。这一研究不仅为一步生成提供了坚实的理论支撑，也为后续自监督学习与生成模型的融合指明了方向。