题目
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
数据范围
1 <= heights.length <=105
0 <= heights[i] <= 104
测试用例
示例1
java
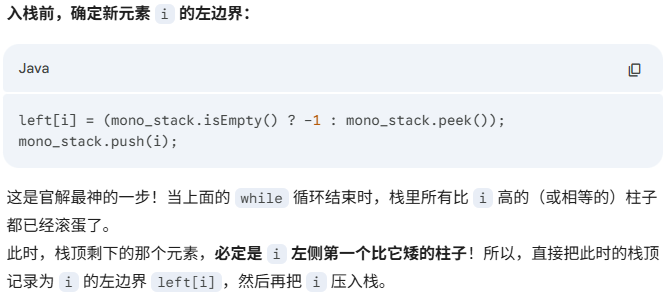
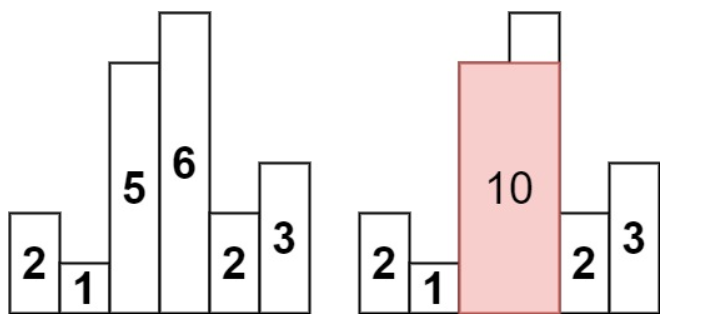
输入:heights = [2,1,5,6,2,3]
输出:10
解释:最大的矩形为图中红色区域,面积为 10示例2
java
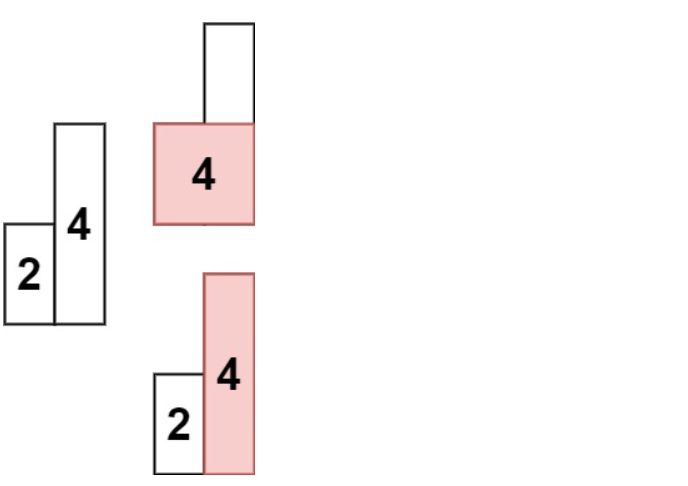
输入: heights = [2,4]
输出: 4题解1(博主题解,时空On,解法与官解1类似,细节不同而已)
java
import java.util.*;
class Solution {
public int largestRectangleArea(int[] heights) {
int len = heights.length;
if (len == 0) return 0;
// left 数组记录的是:当前柱子【右边】第一个比它矮的柱子下标
int[] left = new int[len];
// right 数组记录的是:当前柱子【左边】第一个比它矮的柱子下标
int[] right = new int[len];
// 核心修正1:如果右边没有比自己矮的,右边界默认扩展到数组最右端 (len)
Arrays.fill(left, len);
// 核心修正1:如果左边没有比自己矮的,左边界默认扩展到数组最左端 (-1)
Arrays.fill(right, -1);
Deque<Integer> deque = new LinkedList<>();
// 1. 从左往右遍历,寻找每个柱子的【右边界】
for(int i = 0; i < len; i++){
// 核心修正2:用当前柱子的高度 heights[i] 与栈顶下标对应的高度 heights[deque.peek()] 比较
while(!deque.isEmpty() && heights[i] < heights[deque.peek()]){
// 栈顶元素遇到了比它矮的,它的右边界就确定了,是 i
left[deque.poll()] = i;
}
deque.push(i);
}
deque.clear(); // 清空栈,准备下一次遍历
// 2. 从右往左遍历,寻找每个柱子的【左边界】
for(int i = len - 1; i >= 0; i--){
while(!deque.isEmpty() && heights[i] < heights[deque.peek()]){
// 栈顶元素遇到了比它矮的,它的左边界就确定了,是 i
right[deque.poll()] = i;
}
deque.push(i);
}
int max = 0;
// 3. 计算最大面积
for(int i = 0; i < len; i++){
// 核心修正3:宽度 = 右边界下标 - 左边界下标 - 1
int width = left[i] - right[i] - 1;
int temp = heights[i] * width;
max = Math.max(temp, max);
}
return max;
}
}题解2(官解1,时空同上)
java
import java.util.*;
class Solution {
public int largestRectangleArea(int[] heights) {
int n = heights.length;
// 这里的命名更符合常理:left 存左边界,right 存右边界
int[] left = new int[n];
int[] right = new int[n];
Deque<Integer> mono_stack = new ArrayDeque<Integer>();
// 1. 从左往右找【左边界】
for (int i = 0; i < n; ++i) {
// 把左边所有比当前柱子高(或相等)的都弹走
while (!mono_stack.isEmpty() && heights[mono_stack.peek()] >= heights[i]) {
mono_stack.pop();
}
// 弹干净后,如果栈空了,说明左边没有比我矮的,左边界是 -1;
// 如果栈没空,栈顶剩下的那个就是左边第一个比我矮的柱子。
left[i] = (mono_stack.isEmpty() ? -1 : mono_stack.peek());
mono_stack.push(i); // 自己入栈
}
mono_stack.clear(); // 清空栈
// 2. 从右往左找【右边界】
for (int i = n - 1; i >= 0; --i) {
// 把右边所有比当前柱子高(或相等)的都弹走
while (!mono_stack.isEmpty() && heights[mono_stack.peek()] >= heights[i]) {
mono_stack.pop();
}
// 弹干净后,栈空说明右边没矮的,右边界是 n;否则是栈顶元素。
right[i] = (mono_stack.isEmpty() ? n : mono_stack.peek());
mono_stack.push(i);
}
int ans = 0;
// 3. 计算面积
for (int i = 0; i < n; ++i) {
// 宽度计算公式依旧是:右边界 - 左边界 - 1
ans = Math.max(ans, (right[i] - left[i] - 1) * heights[i]);
}
return ans;
}
}题解3(关节2,时空同上,虽然两级没变,但时空都优于第一种解法)
java
import java.util.*;
class Solution {
public int largestRectangleArea(int[] heights) {
int n = heights.length;
int[] left = new int[n];
int[] right = new int[n];
// 由于右边界是在出栈时确定的,如果有些柱子(比如最矮的)一直不出栈,
// 它的右边界就会缺失,所以必须提前用 n 兜底。
// 左边界是在入栈时确定的,每个元素都会入栈,所以不需要给 left 兜底。
Arrays.fill(right, n);
Deque<Integer> mono_stack = new ArrayDeque<Integer>();
// 仅仅通过一次从左到右的遍历搞定所有事
for (int i = 0; i < n; ++i) {
// 【确定右边界】:遇到比栈顶矮的柱子 i 了
while (!mono_stack.isEmpty() && heights[mono_stack.peek()] >= heights[i]) {
// 栈顶元素被弹出的瞬间,说明它的右边界找到了,就是当前挡路的 i
right[mono_stack.peek()] = i;
mono_stack.pop();
}
// 【确定左边界】:此时栈里比 i 高的已经被清理干净了
// 栈顶剩下的元素,必然是 i 左边第一个比 i 矮的柱子!
left[i] = (mono_stack.isEmpty() ? -1 : mono_stack.peek());
// 记录完左右边界相关的逻辑后,i 安心入栈
mono_stack.push(i);
}
int ans = 0;
// 计算最大面积
for (int i = 0; i < n; ++i) {
ans = Math.max(ans, (right[i] - left[i] - 1) * heights[i]);
}
return ans;
}
}思路
这道题确实有一定的思维难度,但是想懂了以后很简单,以至于这道题因为博主从前做过,导致不到三十分钟就秒杀了,做了那么久对这个方法还是记忆犹新,甚至耗时不如前两个普通题。
我们看数据量,是10的五次方,我们通过普通的暴力根本不可能解决问题,这道题的题解1的思路就是预处理每一个柱状体左右两边,离他最近且小于他的柱子的下标,这样就可以算得这个柱子的高度所能带来的最大面积。
题解二是进阶优化版本,不需要遍历两次预处理,将过程优化为一次,具体解法我就用AI讲解的截图了,因为博主也是现学的,整体代码逻辑修改不大。