直接法 读书笔记 05 第5章 正交方法

第5章：正交方法

解决最小二乘问题最可靠的方法是使用正交变换 。本章讨论基于 Householder 反射和 Givens 旋转的 QR 分解。

5.1 Householder 反射

Householder 反射是一种形式为 的正交矩阵，其中 是标量， 是列向量。可以根据一个向量 来选择 和 ，使得 除了第一个元素 外全为零。MATLAB 函数 [v,beta,s] = gallery('house',x,2) 用于计算 , beta 和 。

对一个长度为 n 的向量 应用 仅需约 4n 次浮点运算：。矩阵 是对称且正交的（），这是由 和 的选择方式决定的。cs_house 函数确保 。它计算 和 ，并用 覆盖 。

double cs_house (double *x, double *beta, int n)
{
    double s, sigma = 0 ;
    int i ;
    if (!x || !beta) return (-1) ;      /* 检查输入 */
    for (i = 1 ; i < n ; i++) sigma += x [i] * x [i] ; /* 计算 x[1..n-1] 的平方和 */
    if (sigma == 0)                    /* x[1..n-1] 全为零 */
    {
        s = fabs (x [0]) ;             /* s = |x(0)| */
        (*beta) = (x [0] <= 0) ? 2 : 0 ;
        x [0] = 1 ;
    }
    else
    {
        s = sqrt (x [0] * x [0] + sigma) ; /* s = ||x|| */
        x [0] = (x [0] <= 0) ? (x [0] - s) : (-sigma / (x [0] + s)) ;
        (*beta) = -1.0 / (s * x [0]) ;
    }
    return (s) ;
}

设 和 分别是向量 和 的非零元模式 。如果 ，那么 。如果这个条件始终成立，稀疏 QR 分解的定理和算法将得到简化，因此下面的讨论假设 是稀疏向量 x 的一个结构性条目 （即 中总是包含 这个位置，尽管其数值可能为零）。那么在忽略数值消去的前提下， 总是成立的。

通常，Householder 反射 不仅会应用于生成它的向量 ，也会应用于其他向量或矩阵。如果将其应用于一个向量 ，并假设 ，那么 的非零元模式将变为：（如果 非空）；否则 。

cs_happly 函数将一个 Householder 反射应用于稠密向量 ，其中 是稀疏的。它用 覆盖 。向量 从矩阵 的第 列获取。

int cs_happly (const cs *V, int i, double beta, double *x)
{
    int p, *Vp, *Vi ;
    double *Vx, tau = 0 ;
    if (!CS_CSC (V) || !x) return (0) ; /* 检查输入 */
    Vp = V->p ; Vi = V->i ; Vx = V->x ;
    for (p = Vp [i] ; p < Vp [i+1] ; p++) /* tau = vᵀ * x */
    {
        tau += Vx [p] * x [Vi [p]] ;
    }
    tau *= beta ;                       /* tau = beta * (vᵀ * x) */
    for (p = Vp [i] ; p < Vp [i+1] ; p++) /* x = x - v * tau */
    {
        x [Vi [p]] -= Vx [p] * tau ;
    }
    return (1) ;
}

5.2 自左向右与自右向左 QR 分解

本节描述两种基于 Householder 的 QR 分解算法，将 m×n 矩阵 分解为正交矩阵 和上三角（若 m < n 则为上梯形）矩阵 的乘积：一种是自左向右 算法，另一种是自右向左算法。

假设 为 m×n 且 。选择一系列 n 个 Householder 反射 将 化为上三角形式。令 表示乘积 。第一个 Householder 反射 根据 的第一列构造，因此 的第一列除对角元 外全为零。第 个 Householder 反射基于向量 ，（长度为 m-k+1）构造，得到标量 和向量 （长度为 m-k+1）。令 是一个长度为 的列向量，其第 1 到 k-1 行元素为零，且 。则 。

定理 5.1 (Golub [113]) ： 的 QR 分解 满足，并且 （因为 是对称正交的）。

Householder 反射序列可以以自左向右 或自右向左 的方式应用。自右向左 算法 qr_right 简单地在每个 Householder 反射构造出来后立即将其应用于整个 。虽然它构成了多 frontal 稀疏 方法的基础，但很难实现为简洁的稀疏矩阵算法。

function [V, Beta, R] = qr_right (A)
    [m, n] = size (A) ;
    V = zeros (m,n) ; Beta = zeros (1,n) ;
    for k = 1:n
        [v, beta, s] = gallery ('house', A (k:m, k), 2) ;
        V (k:m, k) = v ; Beta (k) = beta ;
        A (k:m, k:n) = A (k:m, k:n) - v * (beta * (v' * A (k:m, k:n))) ;
    end
    R = A ;

自左向右 算法 qr_left 一次一列地只将 Householder 反射应用于当前列 ，这对于稀疏情况更易于实现。

function [V, Beta, R] = qr_left (A)
    [m, n] = size (A) ;
    V = zeros (m, n) ; Beta = zeros (1, n) ; R = zeros (m, n) ;
    for k = 1:n
        x = A(:, k) ;                     % 获取第 k 列
        for i = 1:k-1                     % 应用先前已计算的 Householder 反射
            v = V (i:m, i) ;
            beta = Beta (i) ;
            x (i:m) = x (i:m) - v * (beta * (v' * x (i:m))) ;
        end
        % 基于更新后的 x(k:m) 构造新的 Householder 反射
        [v, beta, s] = gallery ('house', x (k:m), 2) ;
        V (k:m, k) = v ; Beta (k) = beta ;
        R (1:(k-1), k) = x (1:(k-1)) ;    % 存储 R 的上三角部分
        R (k, k) = s ;                    % 存储对角元
    end

注意，qr_right 和 qr_left 都不显式计算 的表示；接下来描述的稀疏自左向右 分解也是如此。

5.3 基于Householder的稀疏QR分解

自左向右的QR分解算法（qr_left）构成了下面将要介绍的稀疏QR分解算法的基础。

令 和 分别表示 的第 行和第 列的非零元模式。令 和 分别表示 的第 行和第 列的非零元模式。令 表示 的非零元模式。令 为 的列消去树 （即 的消去树）。

这里陈述的一些定理要求 在结构上是非零的（即，即使数值为零，它也是数据结构中的一个条目）。如果不是这种情况，可以对 的行进行置换，或者通过添加显式的零条目来修改稀疏矩阵 ，以确保这个条件成立。所有定理都忽略了数值消去。有些定理要求矩阵具有强Hall性质（Strong Hall Property）；否则它们提供的是非零元模式的宽松上界。由于篇幅限制，证明是简短的或省略的。强Hall性质的定义在第 7.3 节给出。

定理 5.2 (George, Liu, and Ng [95]) ：考虑 。那么对于 ， 等于 的第 行。对于任何 ， 的非零元模式是

。 (5.1)

也就是说，在 中，任何被 Householder 反射 修改的行 的非零元模式被替换为所有被 修改的行的并集。

证明 ：根据定理 2.1， 的非零模式由 (5.1) 给出。矩阵的条目 （可以忽略 ）非零当且仅当 且 。然后从 中减去矩阵 以得到 ，这会修改所有 的行。 的每个对应行都被用于构造集合并集 (5.1)，因此所有这些行现在都具有相同的非零模式，即由 (5.1) 给出的模式。

定理 5.3 (Golub and Van Loan [114]) ：如果 是正定的，并且其 Cholesky 分解是 ，那么 。

证明： .

定理 5.4 (George and Ng [97]) ：如果对于所有 ， 在结构上非零，那么 。

定理 5.5 (Coleman, Edenbrandt, and Gilbert [22]; George and Heath [83]) ：假设矩阵 具有强 Hall 性质，那么 ，其中 表示 的符号化 Cholesky 因子第 行的非零元模式。如果 不具有强 Hall 性质，则 。

推论 5.6 ：，其中 是 的第 列上三角部分的非零元模式（假设 具有强 Hall 性质）。

一个更简洁的计算 的方法基于以下定理。

定理 5.7 ： (假设 A 有强 Hall 性质)。

证明 ：考虑 的第 列以及 的非零元模式。矩阵 可以写成外积的和，每行一个： 。考虑列 中的条目 。 的非零元模式是 的一个稠密子矩阵；对于 中的任意一对列索引 和 ，每个 都是非零的。根据定理 4.13， 蕴含了在消去树 T 中存在路径 。因此，对于计算 而言， 是冗余的。对于 的第 列中的任何条目 ，只需要考虑 ，即行 i 中非零条目的最小列索引。这个 对应 的第 行中最左边的条目 。因此 。

根据定义，。它可以使用以下两个定理之一计算。

定理 5.8：

,

其中上述表达式中的每个集合互不相交，并且 具有强 Hall 性质。也就是说，

(5.2)

如果 不具有强 Hall 性质，这是 的一个上界。

自左向右的稀疏 算法 cs_qr 使用一个不那么简洁的定理来计算 ，以避免需要计算集合 的大小。

定理 5.9：

(5.3)

其中 具有强 Hall 性质。否则，(5.3) 是一个上界。

这些定理通过一个示例矩阵、其 分解及其列消去树进行了说明。包含 Householder 向量的上三角矩阵 和下三角矩阵 被显示为单个矩阵。出现在 或 中但不在 中的填充元用带圈 表示。

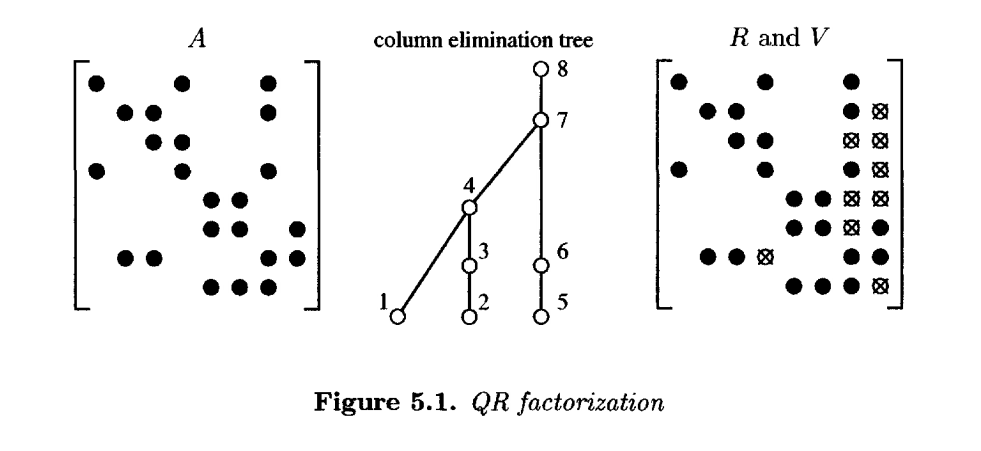
基于这些定理，可以用以下伪代码 sparse_qr_left 来表述一个自左向右的稀疏 分解算法。它假设 在结构上非零，或者等价地，。请将以下伪代码函数与 MATLAB 函数 qr_left 进行比较。

function [V, β_{1...n}, R] = sparse_qr_left(A)
    T = AᵀA 的消去树
    使用 cs_counts 计算 AᵀA 的 |R|
    使用 (5.2) 计算 |V_{1...n}|
    for k = 0 to n-1 do
        R_*k = Reach_{T^k}( { min A_i* | i ∈ A_*k } )
        x = A_*k
        V_k = A_*k
        for each i ∈ R_*k do
            x = x - V_i ( β_i ( V_iᵀ x ) )
            if parent(i) = k then
                V_k = V_k ∪ V_i \ {i}
        R_{1...k-1, k} = x_{1...k-1}
        [v_k, β_k, r_kk] = house( x_{k...m} )

cs_vcount 函数计算 (5.2)。它还计算一个行置换 （由 pinv 表示），以确保对角元 全部在结构上非零，并为所有行 找到leftmost[i] = 。它通过创建和更新一组 n 个链表来找到 。在算法的第 步，链表 将包含集合 。链表通过将每一行 放入链表 来初始化。主 for k 循环计算行置换和 的非零计数。在这个循环中，选择链表 中的第一个条目作为"主元行"；该行成为 的第 k 行，以确保 在结构上非零。如果不存在这样的行，则矩阵 是结构秩亏的，并创建一个虚构行。接下来，除了第一行外，链表 中的所有行都从链表 中移除，并放入 的父节点的链表中。在计算完 后，分配任何未排序的行。它计算 S->lnz，即 V 中的条目数，以及 S->m2，即在添加虚构行后 的行数。

static int cs_vcount (const cs *A, css *S)
{
int i, k, p, pa, n = A->n, m = A->m, *Ap = A->p, *Ai = A->i, *next, *head,
*tail, *nque, *pinv, *leftmost, *v, *parent = S->parent ;
S->pinv = pinv = cs_malloc (m+n, sizeof (int>> ; /* allocate pinv, */
S->leftmost = leftmost = cs_malloc (m, sizeof (int>> ; /* and leftmost */
v = cs_malloc (m+3*n, sizeof (int>> /* get workspace */
if (!pinv II !w II !leftmost)
{
cs_free (w)
return (0) ;
/* pinv and leftmost freed later */
/* out of memory */
}
; nque - w + m + 2*n
/* queue k is empty */
+ m + n
= -1 ;
= -1 ;
= 0
[i] - -1
w + m ; tail = w
k++) head [k]
k++) tail [k]
k++) nque [k]
i++) leftmost
o ; k--)
next = w ; head =
for (k = 0 k < n
for (k = 0 k < n
for (k = 0 k < n
for (i = 0 i < m
for (k = n-1 ; k >=
{
for (p - Ap [k] ; p < Ap [k+1] p++)
{
leftmost [Ai [p]] = k ; /* leftmost[i] = min(find(A(i,:>>)*/
}
}
for (i = m-1
{
i >- 0 i--) /* scan rows in reverse order */
pinv [i] = -1 ;
k = leftmost [i]
if (k == -1) continue
if (nque [k]++ -- 0) tail [k] i
next [i] = head [k] ;
head [k] = i ;
/* row i is not yet ordered */
/* row i is empty */
/* first row in queue k */
/* put i at head of queue k */
}
S->lnz = 0 ;
S->m2 = m ;
for (k = 0 ; k < n k++)
{
/* find row permutation and nnz(V)*/
i = head [k]
S->lnz++ ;
if (i < 0) i - S->m2++ ;
pinv [i] = k ;
if (--nque [k] <= 0) continue
S->lnz += nque [k] ;
if <<pa = parent [k]) != -1)
{
if (nque [pa] == 0) tail [pa]
next [tail [k]] = head [pa]
head [pa] = next [i] ;
nque [pa] += nque [k] ;
/* remove row i from queue k */
/* count V(k,k) as nonzero */
/* add a fictitious row */
/* associate rov i with V(:,k) */
/* skip if V(k+l:m,k) is empty */
/* nque [k] is nnz (V(k+1:m,k>> */
/* move all rovs to parent of k */
tail [k] ;
}
}
for (i = 0 ; i < m i++) if (pinv [i] < 0) pinv [i] k++
cs_free (w) ;
return (1) ;
}

cs_sqr 函数为稀疏 分解执行排序和分析。两个参数决定了 cs_sqr 的行为：order 和 qr。order 参数指定要使用的排序；自然排序（order=0）或 的最小度排序（order=3）是 分解的不错选择。qr 参数对于稀疏 分解必须为真（非零）。cs_sqr 首先找到一个填充约简的列置换 S->q。然后该函数找到置换后的矩阵 （其中 是列置换矩阵，不是正交因子 ），确定 的消去树并对其进行后序遍历，找到 的列计数（等价于 的行计数）。然后调用 cs_vcount 来找到存储 Householder 向量的矩阵 的列计数 。cs_qr 函数执行数值 分解。

css *cs_sqr (int order, const cs *A, int qr)
{
int n, k, ok = 1, *post
css *S ;
if (!CS_CSC (A>> return (NULL)
n = A->n ;
S = cs_calloc (1, sizeof (css>>
if (!S) return (NULL) ;
S->q = cs_amd (order, A)
if (order && !S->q) return (cs_sfree
if (qr)
{
/* check inputs */
/* allocate result S */
/* out of memory */
/* fill-reducing ordering */
(S>> ;
/* QR symbolic analysis */
cs *C = order? cs_permute (A, NULL, S->q, 0) : <<cs *) A) ;
S->parent = cs_etree (C, 1) ; /* etree of C'*C, where C-A(:,q) */
post = cs_post (S->parent, n) ;
S->cp = cs_counts (C, S->parent. post, 1) /* col counts chol(C'*C) */
cs_free (post) ;
ok = C && S->parent && S->cp && cs_vcount (C, S) ;
if (ok) for (S->unz = 0, k = 0 ; k < n ; k++) S->unz +- S->cp [k]
ok = ok && S->lnz >= 0 && S->unz >= 0 ; /* int overflow guard */
if (order) cs_spfree (C) ;
}
else
{
}
S->unz = 4*(A->p [n]) + n
S->lnz - S->unz ;
}
return (ok? S : cs_sfree (S>>
/* for LU factorization only, */
/* guess nnz(L) and nnz(U) */
/* return result S */
csn *cs_qr (const cs *A, const css *S)
{
double *Rx, *Vx, *Ax, *Beta, *x ;
int i, k, p, m, n, vnz, pl, top, m2, len, col, rnz, *s, *leftmost, *Ap, *Ai,
*parent, *Rp, *Ri, *Vp, *Vi, *w, *pinv, *q ;
cs *R, *V ;
csn *N ;
if (!CS_CSC (A) I I IS) return (NULL) ;
m = A->m ; n = A->n ; Ap = A->p ; Ai = A->i ; Ax = A->x ;
q - S->q ; parent - S->parent ; pinv = S->pinv ; m2 = S->m2
vnz = S->lnz ; rnz = S->unz ; leftmost = S->leftmost ;
w = cs_malloc (m2+n, sizeof (int>> ; /* get int workspace */
x = cs_malloc (m2, sizeof (double>> /* get double workspace */
N = cs_calloc (1, sizeof (csn>> ; /* allocate result */



if (!v I I !x I I !N) return (cs_ndone (N, NULL, v, x, 0>> ;
s - v + m2 /* s is size n */
for (k - 0 ; k < m2 k++) x [k] - 0 /* clear workspace x */
N->L - V - cs_spalloc (m2, n, vnz, 1, 0) /* allocate result V */
N->U - R - cs_spalloc (m2, n, rnz, 1, 0) /* allocate result R */
N->B - Beta - cs_malloc (n, sizeof (double>> /* allocate result Beta */
if (!R I I !V I I !Beta) return (cs_ndone (N, NULL, v, x, 0>> ;
Rp - R->p ; Ri - R->i ; Rx - R->x ;
Vp - V->p ; Vi .. V->i ; Vx - V->x ;
for (i - 0 ; i < m2 ; i++) v [i] - -1 /* clear w, to mark nodes */
rnz-O;vnz-O;
for (k .. 0 ; k < n ; k++) /* compute V and R */
{
77
/* R(:,k) starts here */
/* V(:,k) starts here */
/* add V(k,k) to pattern of V */
Rp [k] - rnz
Vp [k] .. p1 - vnz
w[k]-k;
Vi [vnz++] - k ;
top" n ;
col - q ? q [k] : k ;
for (p - Ap [col] ; p < Ap [col+1] ; p++) /* find R(:,k) pattern */
{
i - leftmost [Ai [p]] ;
for (len - 0 ; w [i] !- k
{
s [len++] .. i ;
v [i] - k ;
/* i .. min(find(A(i,q>>) */
i .. parent [i]) /* traverse up to k */
}
while (len> 0) s [--top] .. s
i - piny [Ai [p]]
x [i] - Ax [p]
if (i > k && v [i] < k)
{
Vi [vnz++] - i
w [i] - k ;
}
[--len] ; /* push path on stack */
/* i-permuted rov of A(:,col) */
/* x (i) - A(:,col) */
/* pattern of V(:,k) - x (k+1:m) */
/* add i to pattern of V(:,k) */
}
for (p - top; P < n p++) /* for each i in pattern of R(:,k) */
{
cs_scatter (V, i, 0, v, NULL, k, V, vnz);
i - s [p] ;
cs_happly (V, i, Beta [i), x)
Ri [rnz] .. i
Rx [rnz++] - x [i] ;
x [1] - 0 ;
if (parent [i] -- k) vnz
}
for (p - p1 ; P < vnz ; p++)
/* R(i,k) is nonzero */
/* apply (V(i),Beta(i>> to x */
/* R(i,k) - xCi) */
/* gather V(:,k) - x */
{
Vx [p] .. x [Vi [p]]
x [Vi [p]] - 0
}
Ri [rnz] - k /* R(k,k) .. norm (x) */
Rx [rnz++] .. cs_house (Vx+p1, Beta+k, vnz-p1) ; /* [v,beta]-house(x) */
}
}
Rp [n] - rnz ;
Vp [n] - vnz ;
return (cs_ndone (N, NULL, v, x, 1>>
/* finalize R */
/* finalize V */
/* success */

cs_qr 函数使用由 cs_sqr 计算的符号分析：列消去树 S->parent、列预排序 S->q、行置换 S->pinv、S->leftmost 数组、 和 中的非零元数量（分别为 S->unz 和 S->lnz），以及如果 是结构秩亏时添加虚构行后的行数 S->m2。

该函数首先提取 的内容，分配结果 ，并分配和初始化一些工作空间。接下来，计算 和 的每一列 。for k 循环的主体首先确定 V(:,k) 和 R(:,k) 的起始位置，并找到对应于 C(:,k) 的列 A(:, col)。使用符号化稀疏三角求解（定理 5.7）找到 的第 列的非零元模式 。将先前的 Householder 反射应用于列 k，每个 中的非零条目对应一个反射，并计算 （根据 (5.3)）。修改后的列 从其稠密向量表示 中被收集为 的第 列，并用第 个 Householder 向量覆盖。一个完整的符号化和数值化 分解，包括填充约简的列预排序，可以通过 S=cs_sqr(3, A, 1) 后跟 N=cs_qr(A, S) 来计算。

在 MATLAB 中，[Q,R]=qr(A) 计算 的 分解。填充约简的列置换必须在调用 qr 之前应用于 A。MATLAB 的 qr 函数基于 Givens 旋转，而不是 Householder 反射。它返回正交矩阵 ，而不是 cs_qr 使用的更紧凑的 V、Beta 和 pinv 表示。

cs_qright 和 cs_qleft M 文件将 Householder 反射（由 cs_qr 计算的 V、Beta 和 p）应用于矩阵的右侧或左侧。cs_qleft 类似于 cs_happly，不同之处在于它应用所有的 Householder 向量。

function X = cs_qright (V, Beta, p, Y)
%CS_QRIGHT apply Householder vectors on the right.
% X = cs_qright(V,Beta,p,Y) computes X = Y*P'*Hl*H2* ... *Hn = Y*Q where Q is
% represented by the Householder vectors V, coefficients Beta, and
% permutation p. p can be [], which denotes the identity permutation.
% To obtain Q itself, use Q = cs_qright(V,Beta,p,speye(size(V,l))).
%%
See also CS_QR, CS_QLEFT.
[m n] = size (V) ;
X- Y ;
if (-isempty (p)) X = X (:,p) ; end
fork-l:n
X = X - (X * (Beta (k) * V (:,k))) * V (:,k)'
end
function X = cs_qleft (V, Beta, p, Y)
%CS_QLEFT apply Householder vectors on the left.
% X- cs_qleft(V,Beta,p,Y) computes X = Hn* .•. *H2*Hl*P*Y = Q'*Y where Q is
% represented by the Householder vectors V, coefficients Beta, and
% permutation p. p can be [], which denotes the identity permutation.
%%
See also CS_QR, CS_QRIGHT.
[m2 n] - size (V)
[m ny] = size (Y)
X = Y ;
if (m2 > m)
if (issparse ())
x s [X sparse(m2-m,ny)]
else
X = [X
end
end
if (-isempty (p>> X = X (p,:) ; end
fork=l:n
X = X - V (: ,k) * (Beta (k) * (V (:,k)' * ))
end

存储在 V 中的 Householder 向量通常比 的显式表示要稀疏得多。在 MATLAB 中尝试这个简短的实验，它比较了 （有 38,070 个非零元）和 （只有 3,906 个非零元）：

load west0479
q = colamd (west0479)
[Q,R] = qr (west0479 (:,q))
[V,beta,p,R2] = cs_qr (west0479 (:,q)) ;
Q2 = cs_qright (V, beta, p, speye(size(V,1)))

5.4 Givens 旋转

Givens 旋转是一个 2×2 的正交矩阵，可以应用于 2×1 的向量，以将选定元素化为零。如果 a 和 b 是标量，则选择 c 和 s 使得：

其中 。系数 c 和 s 使用下面的 givens2 MATLAB 函数计算。

function g = givens2(a, b)
    if (b == 0)
        c = 1 ; s = 0 ;
    elseif (abs(b) > abs(a))
        tau = -a / b ;
        s = 1 / sqrt(1 + tau^2) ;
        c = s * tau ;
    else
        tau = -b / a ;
        c = 1 / sqrt(1 + tau^2) ;
        s = c * tau ;
    end
    g = [c, -s ; s, c] ;

如果应用于一个 2×n 的稀疏矩阵 （等价于从一个更大的矩阵中选取两行），则 中每一行的非零元模式都等于 中这两行非零元模式的并集 ，除了可以特意选择将 中的某个特定元素化为零。

5.5 行合并稀疏 QR 分解

对于一个稠密矩阵，基于 Givens 旋转的 分解所需的浮点运算量比基于 Householder 反射的 分解多 50%，但在稀疏情况下它有一些优势。可以通过对行进行排序，使得工作量低于基于 Householder 的稀疏 。使用 Givens 旋转的缺点是，所得的 分解不太适合用于多 frontal 技术。

MATLAB 的稀疏 分解使用 Givens 旋转。它操作于 和 的行上。矩阵 初始时为零，但分配了足够的空间来容纳最终的 。分解的每一步引入 的一个新行，并利用现有的 消去其元素，直到该行全部为零或可以成为 的新行为止。用于稠密矩阵的 qr_givens_full 算法如下所示。它假设 的对角线非零。最内层循环通过一个作用于传入的 的第 行和 的第 行的 Givens 旋转来消去 元素。

function R = qr_givens_full (A)
    [m, n] = size (A) ;
    for i = 2:m
        for k = 1:min(i-1, n)
            A([k i], k:n) = givens2 (A(k, k), A(i, k)) * A([k i], k:n) ;
            A(i, k) = 0 ;
        end
    end
    R = A ;

对于稀疏情况，如果要消去的 已经为零，则可以跳过该旋转操作。需要被消去的元素 对应于 Householder 矩阵 的第 行的非零元模式 ，这在前一节已讨论。

定理 5.10 (George, Liu, and Ng [95]) ：假设 A 有一个无零对角线。那么 Householder 矩阵 的第 行的非零元模式 由 的消去树 中的路径 给出，其中 是第 行中最左边的非零元素， 是树的根节点。

这个方法在下面的 qr_givens M 文件中进行了说明。

function R = qr_givens (A)
    [m, n] = size (A) ;
    parent = cs_etree (sparse (A), 'col') ; % 计算 AᵀA 的消去树
    A = full (A) ; % 转换为稠密矩阵（仅为演示，效率不高）
    for i = 2:m
        k = min (find (A (i, :))) ; % 第 i 行最左边的非零列 f
        if (isempty(k))
            continue ; % 跳过全零行
        end
        while (k > 0 && k <= min (i-1, n)) % 沿消去树路径向上遍历
            A([k i], k:n) = givens2 (A(k, k), A(i, k)) * A([k i], k:n) ;
            A(i, k) = 0 ;
            k = parent (k) ; % 移动到父节点
        end
    end
    R = sparse (A) ;

这个 M 文件并非一个高效的实现。由于对稀疏矩阵的行进行操作非常慢，它首先将矩阵转换为稠密矩阵。在一个高效的实现中，只会将 的第 行存储在一个大小为 的工作数组中。矩阵 被分配了足够的空间来容纳最终的每一行，但初始为空。将 的第 行与消去树路径 上的行 进行消去，直到遇到一个空的 行 为止，此时消去停止，并且部分消去的 行成为 的第 行。如果 有一个无零对角线，这将在 时发生。这个方法被称为行合并 QR 分解算法 ；也可以被称为自底向上稀疏 QR ，因为在第 步，它只访问 的第 行以及 的第 1 到 行。qr_givens 函数假设 具有无零对角线。

5.6 延伸阅读

George 和 Heath [83] 提出了 Givens 旋转的行合并算法；MATLAB 中的 qr 函数是 Gilbert 对该方法的实现。Liu [149] 的行合并方案是对 George-Heath 方法的推广。George 和 Liu [90] 比较了用于稀疏 分解的 Householder 反射和 Givens 旋转。Heath [128] 综述了解决稀疏线性最小二乘问题的一系列方法。Givens [112] 和 Householder [138] 讨论了后来以他们名字命名的变换。Householder 反射、Givens 旋转、 分解和 Gram-Schmidt 方法在 Golub 和 Van Loan [114]、Higham [135] 以及 Stewart [190] 的著作中都有详细讨论。

许多论文研究了 、 和 Householder 矩阵 的稀疏模式以及表示它们的数据结构。Coleman、Edenbrandt 和 Gilbert [22] 证明了当 具有强 Hall 性质时，一系列符号化 Givens 旋转给出了 结构的紧上界。George、Liu 和 Ng [95] 描述了一种利用消去树中的路径来存储 Householder 矩阵 的高效数据结构。Gram-Schmidt 方法在稀疏情况下通常不被使用，因为它显式地计算 ，而显式的稀疏 比 Householder 矩阵 有更多的非零元。Ng 和 Peyton [158] 描述了一种用于显式稀疏 的高效数据结构。

稀疏多 frontal QR 分解通常基于 Householder 反射；参见 Lu 和 Barlow [154]、Matstoms [156]、Amestoy、Duff 和 Puglisi [6] 以及 Pierce 和 Lewis [167]（后者还提出了一种近似秩揭示多 frontal QR 算法）。

欠定系统可以通过将 QR 分解应用于 来求解，如 George、Heath 和 Ng [84] 所述。

练习题

5.1. 编写一个计算 和 的非零元模式的函数。

5.2. 修改 cs_qr，使其能够处理 m < n 的 m×n 矩阵。一个简单的解决方案是在 后面添加空行，但如果 m 远小于 n，这将效率不高。

5.3. 编写一个函数 cs_reqr(cs *A, css *S, csn *N)，用于计算 分解。它应假设 和 的非零元模式已经计算好。

5.4. 在 cs_qr 中添加列主元法。如果某列的范数小于或等于给定的容差，则将其置换到矩阵的末尾。矩阵 和 将需要动态重新分配（见第 6 章的 cs_lu），因为置换列破坏了符号化预分析。

5.5. 在 cs_sqr 中将后序排序与填充约简排序相结合（详见习题 4.9）。