目录
变压器无处不在,它是电网的基石、是小型电子设备的能量枢纽。上篇文章我们从电磁感应定律出发,逐步探究了耦合电感的工作原理,但是具体的耦合电感(变压器)分为哪几种,又有什么区别,并不了解。
本文将带你踏上一段化繁为简的旅程,揭示分析变压器的三层核心思维:
-
第一层:解耦之道------反射阻抗。面对最一般的空心变压器,我们将学习"反射阻抗"这一强大工具,它如何将复杂的互感电路,等效为一个简单的无源电路,让我们绕过联立方程。
-
第二层:抓住本质------全耦合与变比 。当耦合趋于完美(k=1),一个更简洁的规律浮出水面:电压与匝数成正比。我们将看到,如何由此衍生出阻抗变换的能力,这是理解变压器功能的关键一跃。
-
第三层:终极简化------理想变压器模型 。在理论分析和初步设计中,我们追求极致的简洁。通过引入三个理想化条件,我们得到电路理论中最优雅的元件之一:理想变压器。它只剩下一个参数------变比n,却蕴含着电压、电流、阻抗变换的全部奥秘。
理解这三层模型,不仅是为了解题,更是为了获得一种分而治之的工程视角:在面对实际问题时,你能迅速判断该用哪种"镜头"去观察眼前的变压器。让我们开始吧。
一、空心变压器的反射阻抗
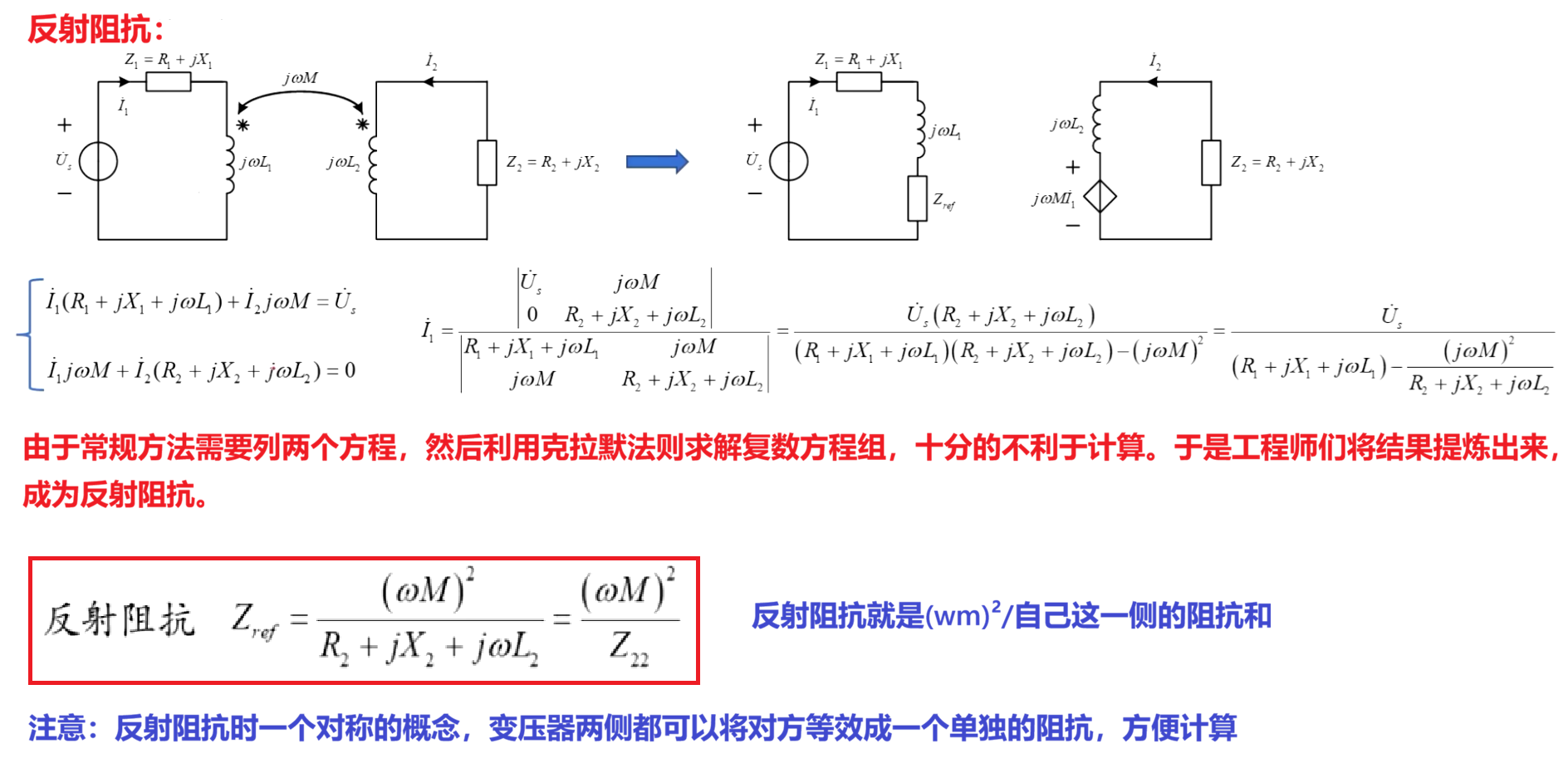
(1)反射阻抗的基本概念
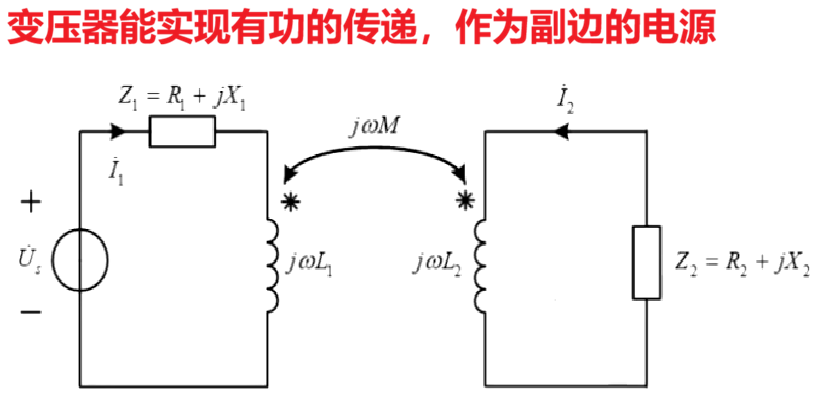
空心变压器指的是一对只有耦合关系,却没有任何导线直接相连的耦合电感。根据上篇文章最后分析的:变压器可以传递有功、变换无功。所以变压器可以当做一个有功的桥梁,在无独立源的副边看来,耦合电感就是一个电源。
 (2)戴维南定理在反射阻抗中的运用
(2)戴维南定理在反射阻抗中的运用
前面我们推导的反射阻抗是在"原边有独立源,副边无独立源"情况下推导的,但是万一两边都有独立源呢?
此时可以用叠加定理的思想,分别将两侧独立源置零,利用两次反射阻抗计算出总电流,然后叠加即可。但是略微有点麻烦,不过人们发现戴维南定理似乎也能在这个时候发挥作用,从而将两次计算简化为一次。
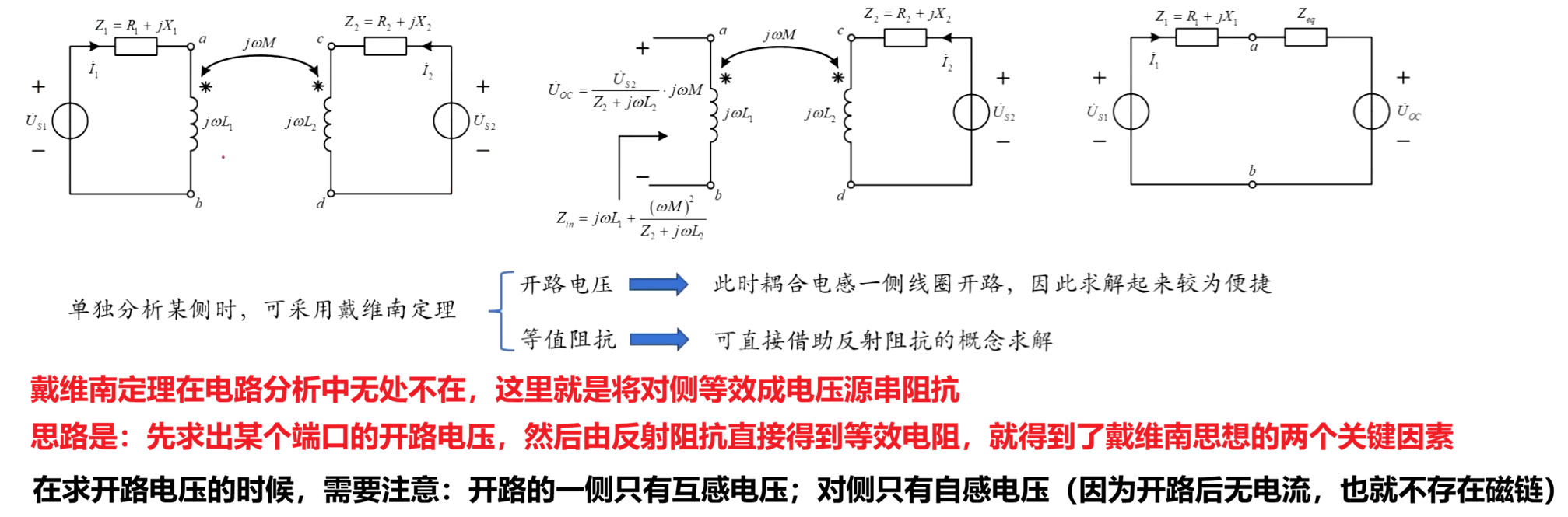
不过值得注意的是:戴维南思想仅仅是将一侧等效成电压源串阻抗的方法,只能用于单独分析某一侧的电路变量。如果需要两侧都分析则没什么优势(可能在高手中依旧是戴维南定理更加好用,不过我更喜欢叠加定理),毕竟直接使用叠加定理更加直观简洁。
二、全耦合变压器
(1)全耦合变压器的基本概念
全耦合变压器本质就是空心变压器的一种特殊形式:将空心变压器中插入一个铁芯,则磁通量几乎100%通过铁芯到另一侧电感,而没有任何损耗。所以耦合系数K=1。
正是因为全耦合变压器是空心变压器的特殊形式,那么空心变压器的分析方法如:反射阻抗、戴维南等效变换等都可以直接套用。不过由于耦合系数K=1,所以会延伸出两个关键特点:变比固定、阻抗变换。
这个我们在下面详细讲解。
(2)变比固定
所谓的变比,指的是两侧各电路参数的变换比值,并不是说这个比值会变化。相反的,只要一个电路的匝数确定了,那么变比的值就是恒定不变的。
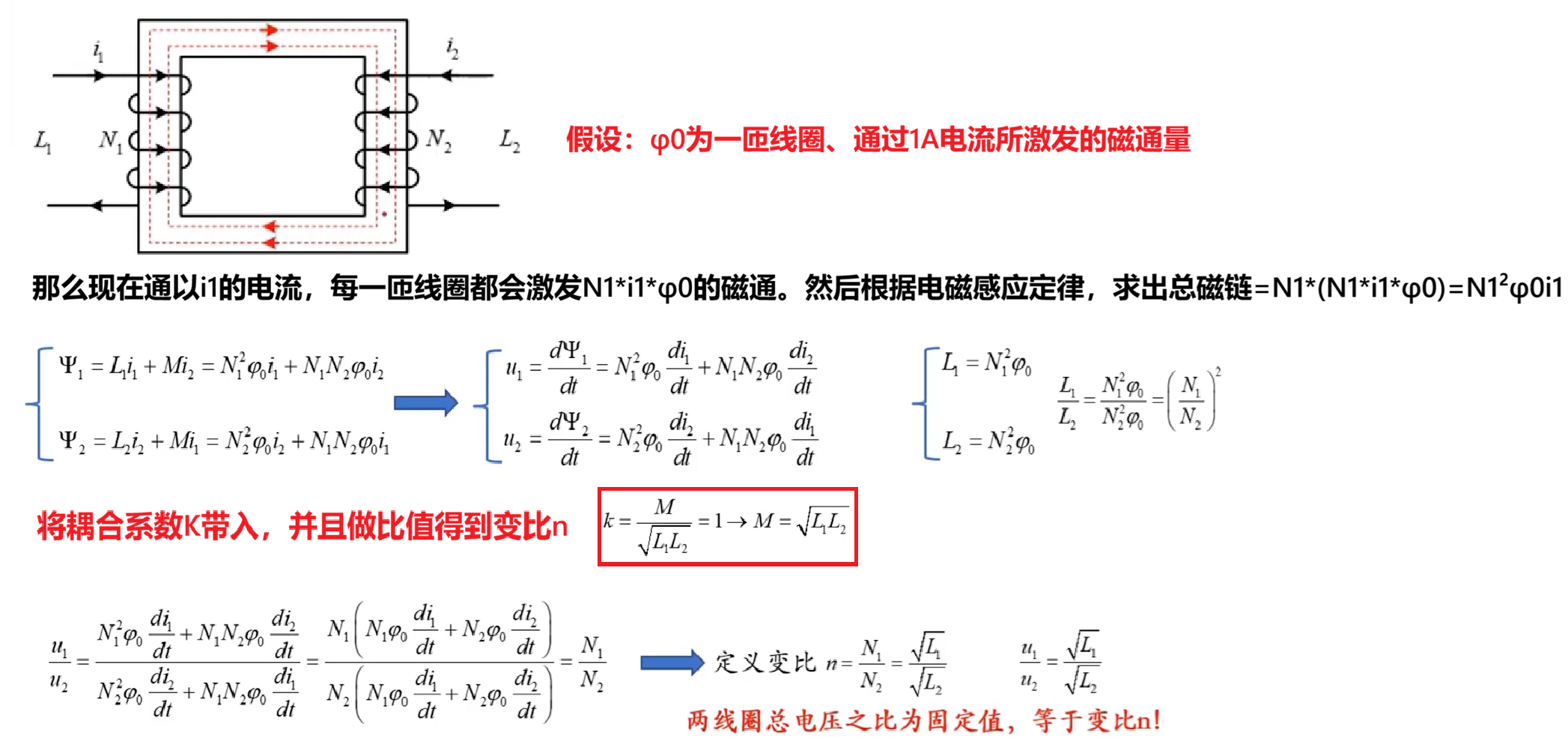
关于变比,他能够反映变压器两端各个信息的变换关系:匝数比、电感比开根号、电压比、电流比等等。
(3)阻抗变换
正是由于全耦合变压器的耦合系数K=1,以及变比n为固定值的特点,引申出变压器两边可以进行阻抗变换的结论,用以简化电路结构。
阻抗变换的本质是使用空心变压器中反射阻抗的结论,进一步推导出来的二级结论。
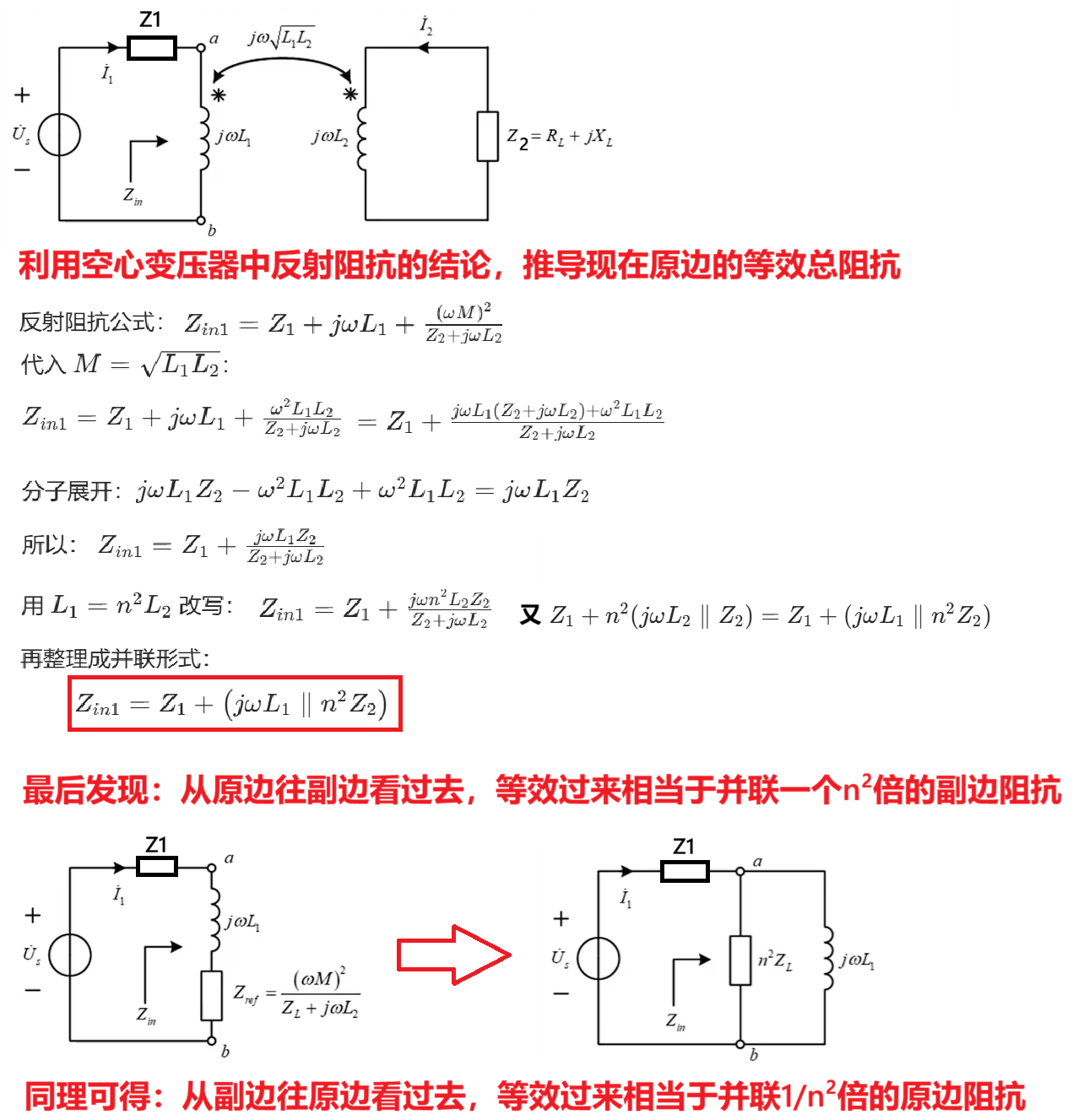
千万要注意:反射阻抗套用的是右边整个回路所有的阻抗(包括电感本身的阻抗);而利用全耦合变压器中的阻抗变换时,只考虑副边的负载阻抗,与电感阻抗无关。
不过值得注意的是:在全耦合变压器中的阻抗变换时,原副变换的系数是相反的,这一点与反射阻抗两边等价的思想也是相反的。
比如副边等效到原边,则是副边阻抗乘上n²倍;而原边阻抗等效到右边,则是原边阻抗除以n²倍。
但无论如何,阻抗变换到对侧,都是并联。
(3)由变比固定引出的比例关系
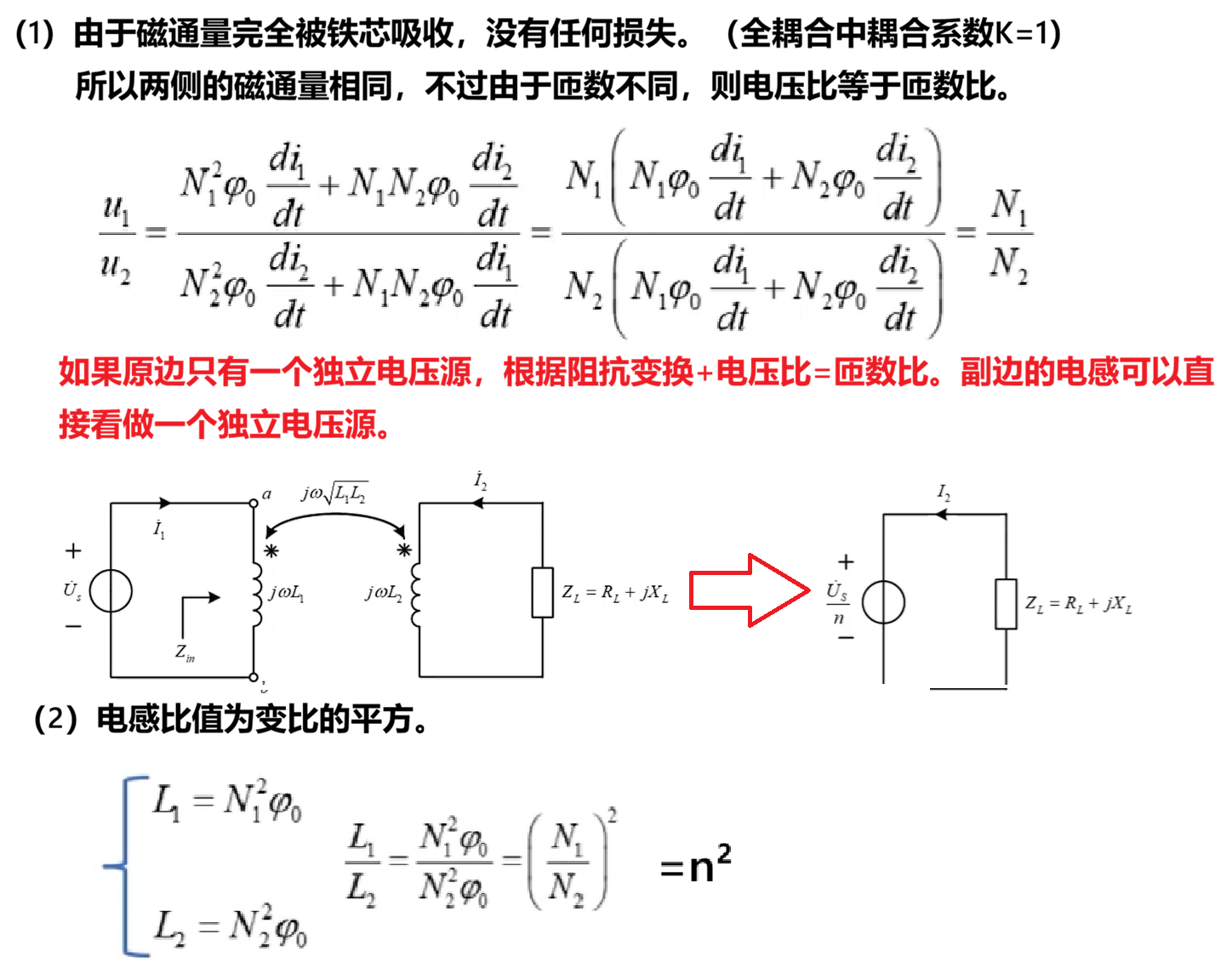
三、理想变压器
(1)理想变压器的基本特点
理想变压器本质就是将全耦合变压器的某些参数理想无穷化。理想变压器中的电感参数L1、L2都被认为是趋近于无穷大的,且他们之间原本满足的变比关系仍然保持不变。
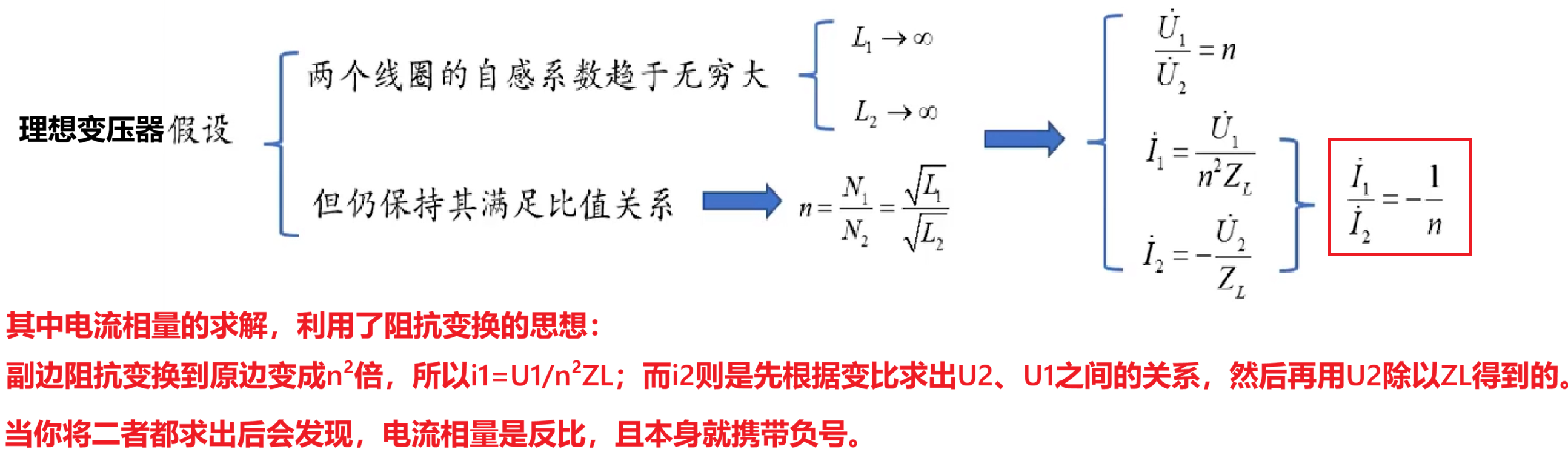
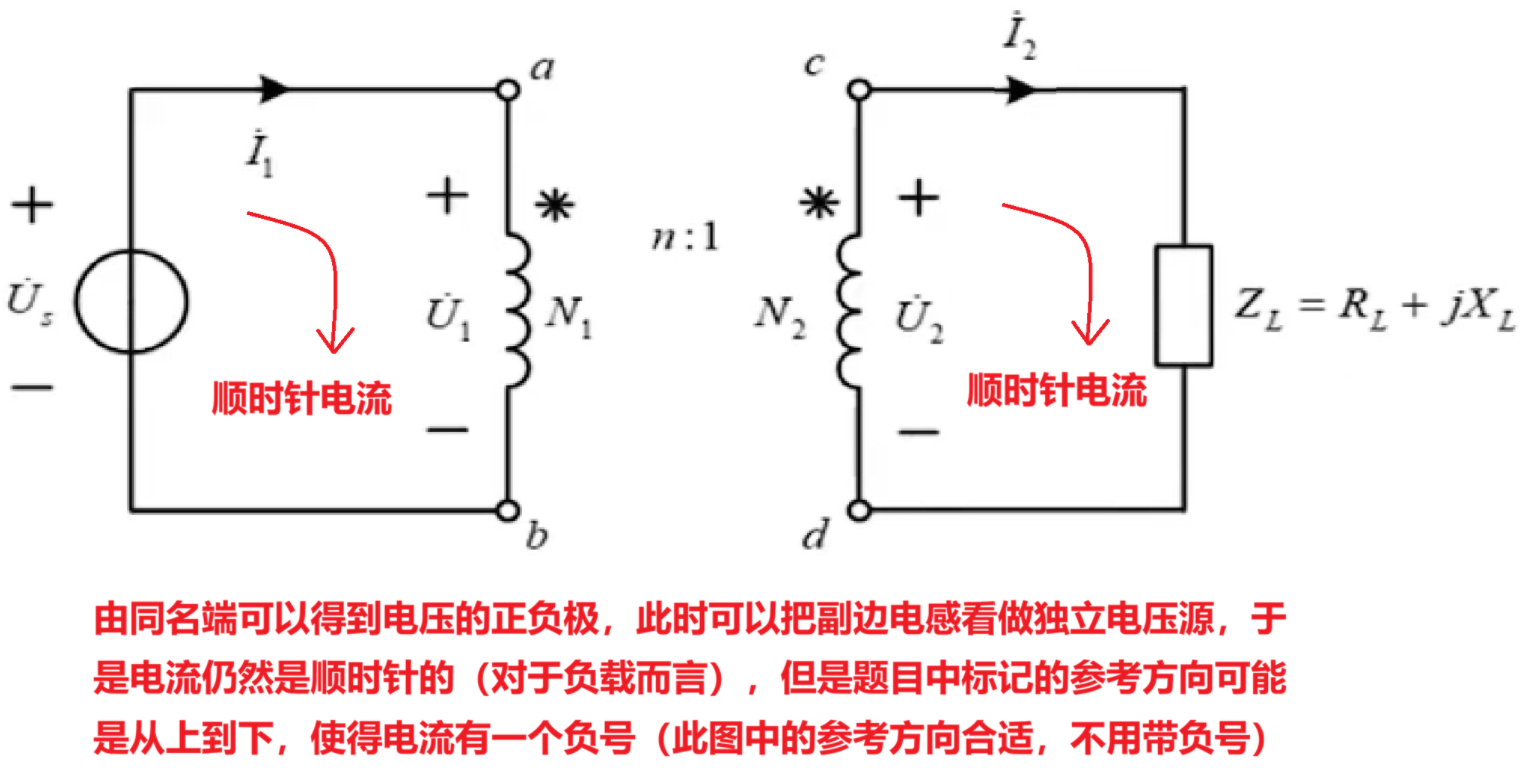
虽然我这里公式中强调了电流方向本身有负号的问题。但是其实你并不需要记忆,还记得我们之前说的同名端吗:如果两个都是同名端流入,则两端都是正号,这里指的是电压的极性。电流的方向通过电压极性往负载上看过去,可以得到流向。
此时就需要把耦合电感看做一个独立源即可,我们说的电流方向是对外负载而言(因为负载上的电流方向与电源内部是相反的)
我这样理解可能与书上有所差异,但是我觉得书上的理解方式不够直观,十分晦涩难懂。直接先用同名端判断电压方向,然后顺着电压直接得到电流方向不就可以行了嘛。
(2)理想变压器引出的电流比例关系
在空心变压器中仅仅只有反射阻抗的结论可以使用、到了全耦合变压器则引入了阻抗变换、电压比=变比、电感比=变比²等结论。
**最后在理想变压器部分又补充了电流比=变比的倒数这个结论。**是一个逐步完善逐步简化计算的过程。


简单来说就是,为了建立这个中间传递能量的磁场,需要消耗一定的功率。而所有变压器消耗的功率都由电流体现(电流始终无法达到无消耗时的最大值,被电感缓存了,虽然没有消耗有功),只不过在理想变压器中,这个电流无穷小,看似没有消耗电流最大值。
(3)理想变压器的阻抗变换
由于理想变压器脱胎于全耦合变压器,那么全耦合变压器拥有的阻抗变换功能理想变压器也会拥有。
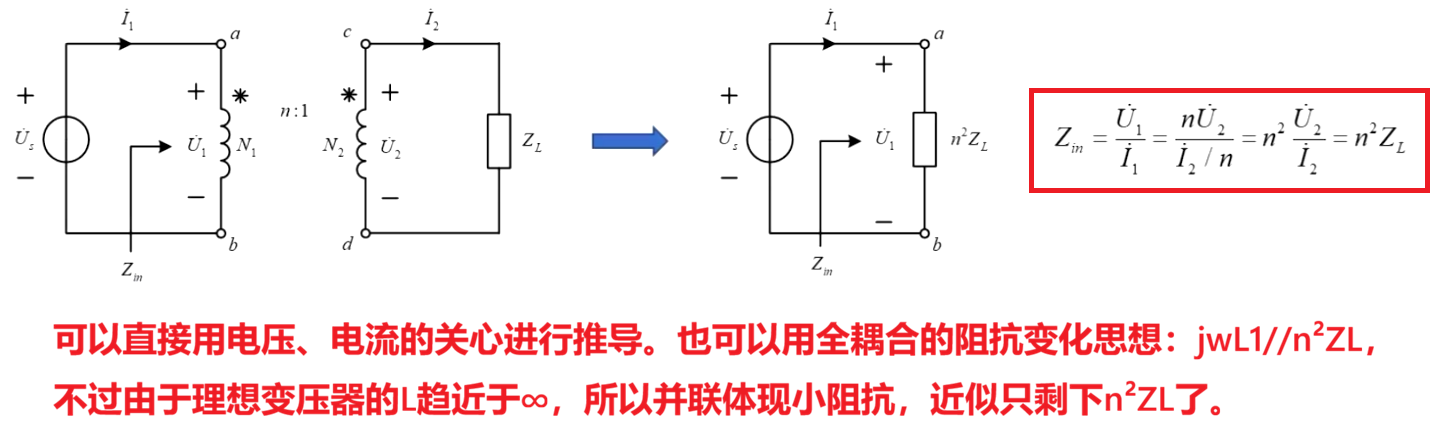
理想变压器的阻抗变换功能通常会用在负载阻抗匹配中,使得负载ZL获得最大的有功功率。(共轭匹配、共模匹配)。不过理想变压器由于不会改变阻抗角,所以在原本负载与电源Ns的内阻不匹配时,只能用于共模匹配。
而全耦合变压器由于自身携带电感的阻抗,所以不方便准确匹配。
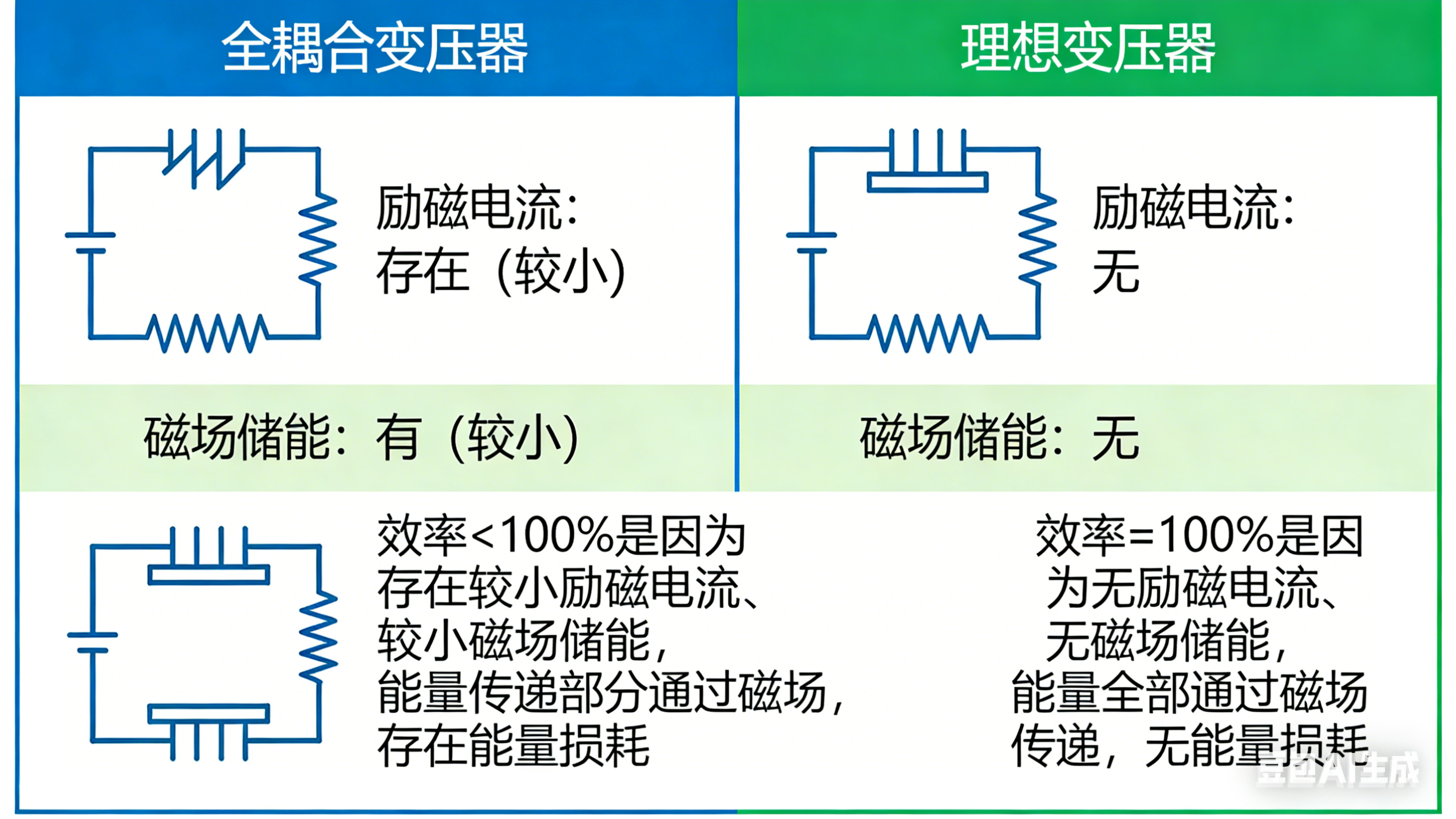
四、理想变压器的空转电流(励激电流)、储能功能的理解
在两个耦合电感之间能量的传递,是依托于媒介磁场的。而由于电磁感应定律,媒介磁场的建立需要消耗一定量的电流,于是当一个变化的电流(比如正弦稳态电流)流过电感的时候,会产生一定程度的衰减,也就形成了电感相位变化。
这个衰减的电流我们认为他用来空转建立磁场了,虽然建立磁场的过程不会消耗能量,但是起到一个缓存作用,使得原边的电流不能完完全全流入副边,这也是全耦合变压器的电流不满足n倍比例关系的原因。
而在电磁场、物理学科中。会研究励激电流与电感的关系。在这里我只是给出记忆一下,不需要证明:电感越大,励激电流越小。即电感越大,用来空转的电流也就越小,而磁场能本身就是这个空转电流做的无功。
在理想变压器条件下,耦合电感趋近于∞,所以空转电流为0,磁场储能为0。此时可以认为理想变压器只做了功率传递、电压、电流幅值变换的功能。而传统电感的储能作用完全消失。所以在理想变压器的题目中,是万万不能用去耦等普通耦合电感的分析方法。此时你只需要将理想变压器当做一个独立的元件即可。