文章目录
1、定点数除法的常用算法
定点数除法通常采用逐位相除的方法，类似于手工长除法，但在计算机中需要通过加减和移位操作实现。主要算法有原码除法和补码除法，其中原码除法又分为恢复余数法和不恢复余数法（加减交替法）。补码除法则常用补码加减交替法。
2、原码除法
2.1、步骤
符号位单独处理：商的符号 = 被除数符号 ⊕ 除数符号（异或）。
数值部分取绝对值进行无符号除法。
最后将商的符号与数值组合。
2.2、恢复余数法
2.2.1、原理
模仿手算，每次用当前余数减去除数，若够减（余数≥0），商上1；若不够减（余数为负），商上0，并恢复原来的余数（加上除数）。然后余数左移一位，继续下一步。
2.2.2、缺点
当不够减时需恢复余数，多了一次加法，效率较低。
2.2.3、步骤
先看题目：
描述：
| 符号 | 符号说明 |
|---|---|
| Y* | 除数Y的绝对值 |
| -Y\*补 | -Y*的补码 |
 |
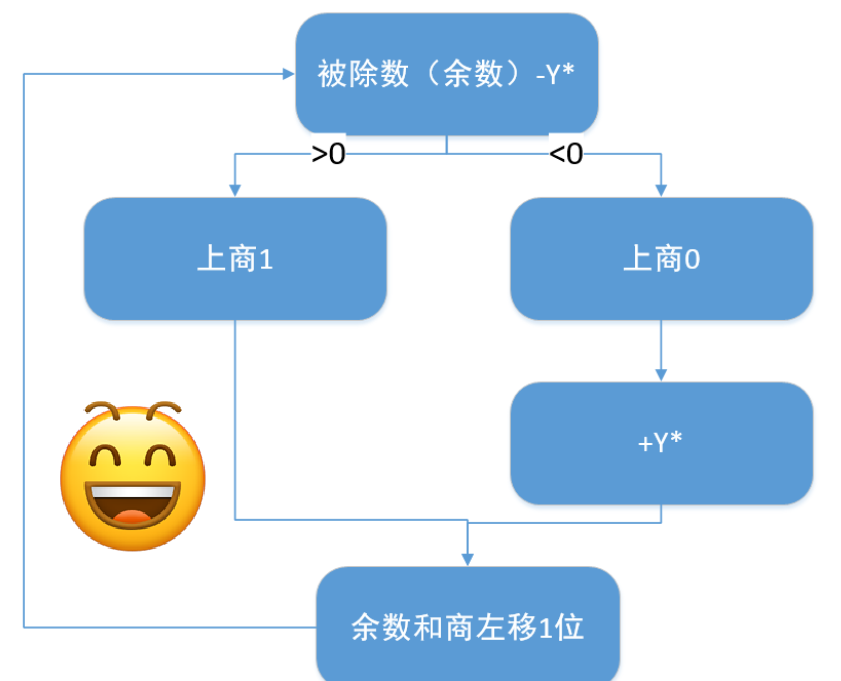当左移次数和除数Y的位数一致时，结束。
看例题：
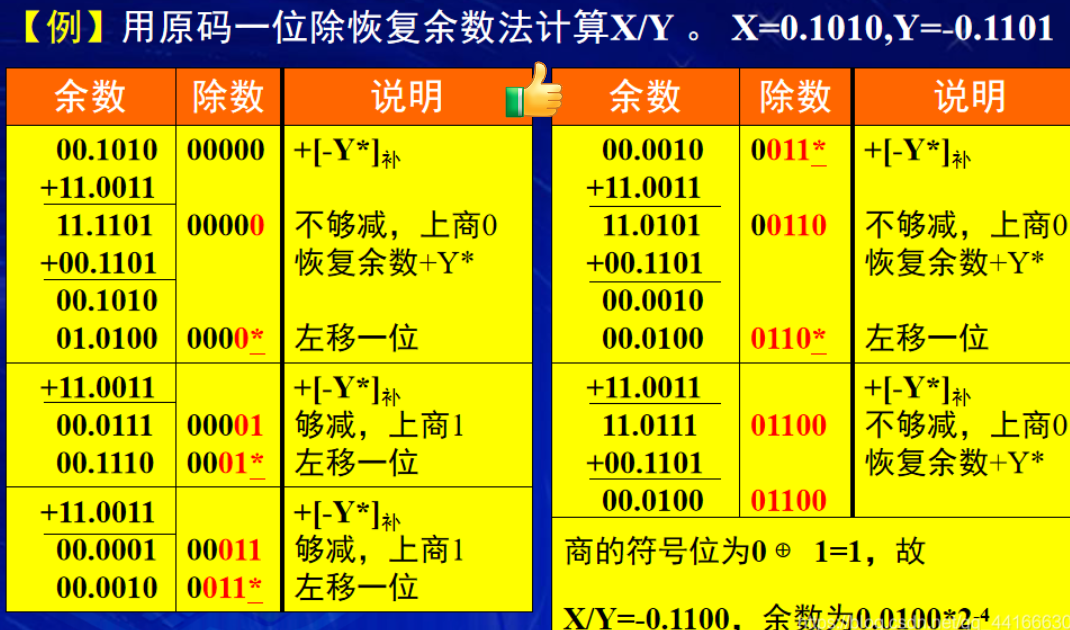
易错点：
若最后一步上商0（即余数小于0），则还需进行一次恢复余数，即余数再加Y*，才能得到正确的余数。
2.2.4、参考视频
看不懂文字的推荐到这个视频学习：
原码除法 恢复余数法和不恢复余数法(加减交替法) 计组
【细碎知识2】定点数的乘除运算（原码一位乘、恢复余数法、加减交替法）
2.3、不恢复余数法（加减交替法）
2.3.1、核心思想
不恢复余数法的核心在于：当某一步试减发现不够减（余数为负）时，不立即恢复余数，而是带着这个负的余数继续下一步，但下一步的操作由"减法"改为"加法"。
通过数学推导可以证明，这种"加减交替"的结果与"先恢复再左移后试减"的结果是完全等价的。
2.3.2、步骤（设被除数、除数均为n位无符号数）
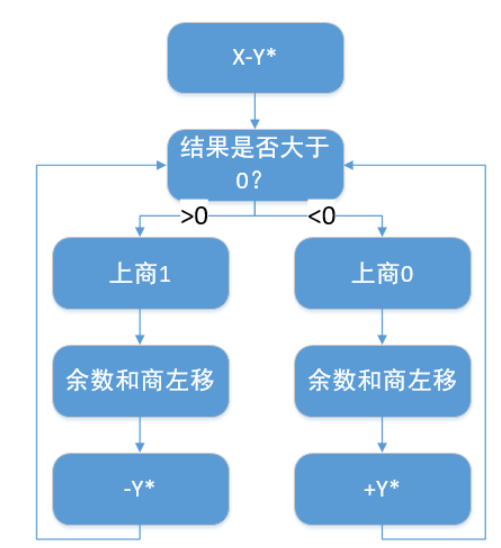结束条件也是：当左移次数=被除数的位数时，结束。
易错点：
若最后一步上商0（即余数小于0），则还需进行一次恢复余数，即余数再加Y*，才能得到正确的余数。
2.3.3、优缺点
2.3.3.1、优点
速度快：去掉了"恢复"所需的额外加法操作，每一步固定一次加法或减法，执行时间确定且更短。
控制逻辑统一：非常适合硬件流水线实现。
2.3.3.2、缺点
最后可能需要修正：如果最终余数为负，需要加一次除数来得到正确的正余数。
理解难度稍高：相对于恢复余数法，加减交替的逻辑在概念上没有那么直观。
2.2.4、参考视频
看不懂文字的推荐到这个视频学习：
原码除法 恢复余数法和不恢复余数法(加减交替法) 计组
【细碎知识2】定点数的乘除运算（原码一位乘、恢复余数法、加减交替法）
3、补码除法（加减交替法）
3.1、补码除法介绍
这种算法相对于原码除法的核心优势在于：商符在运算过程中自动形成，不需要单独处理符号位，并且将操作数的加减统一为补码加法运算，简化了控制逻辑。
3.2、算法前提
被除数 和 除数 都用补码表示。
运算过程中涉及双符号位（变形补码），以防止溢出并方便判断余数的正负。
3.3、核心运算规则
补码除法与常见的原码恢复余数法逻辑不同。它的每一步是加还是减，取决于被除数（余数） 和 除数 的符号关系。
规则表如下：
| 步骤 | 判断条件 （余数 R 与 除数 D 的符号关系） | 操作 | 商上 （上商规则） |
|---|---|---|---|
| 第一步 | 同号 | 做减法：R=R−D | 商上 1 |
| 第一步 | 异号 | 做加法：R=R+D | 商上 0 |
| 后续步 | 新余数 与 除数 同号 | 左移一位后，做减法：R=2R−D | 商上 1 |
| 后续步 | 新余数 与 除数 异号 | 左移一位后，做加法：R=2R+D | 商上 0 |
3.4、计算过程
