文章目录
- 1、浮点数加减运算
-
- 1.1、对阶(Alignment)
- 1.2、尾数加减
- 1.3、规格化(Normalization)
- 1.4、舍入(Rounding)
- 1.5、判断溢出
- [1.6 、参考视频](#1.6 、参考视频)
- 2、浮点数乘法运算
-
- 2.1、乘法运算步骤
-
- 2.1.1、符号位计算
- [2.1.2、 指数部分计算](#2.1.2、 指数部分计算)
- 2.1.3、尾数部分计算
- 2.2、参考视频推荐
- 3、浮点数除法运算
-
-
- 3.1.1、符号位计算
- [3.1.2、 指数部分计算](#3.1.2、 指数部分计算)
- 3.1.3、尾数部分计算
-
1、浮点数加减运算
1.1、对阶(Alignment)
目标:使两个数的指数相同,以便尾数直接相加。
方法:
1、比较两个数的指数,找出较小的指数。
2、将较小指数的数的尾数右移(相当于除以2的差值次方),同时增加其指数,直到两数指数相同。
3、右移过程中,低位丢弃可能导致精度损失(称为"右移丢失")。
示例:
计算 1.0 × 2⁰ + 1.0 × 2⁻¹
指数差:0 - (-1) = 1
将 1.0 × 2⁻¹ 的尾数右移1位 → 0.1 × 2⁰
现在两数均为 1.0 × 2⁰ 和 0.1 × 2⁰。
1.2、尾数加减
根据符号位决定执行加法或减法:
1、同号相加:直接相加尾数。
2、异号相减:尾数相减,结果的符号由绝对值较大的数决定。
溢出处理:若尾数结果超出范围(如单精度>2.0或<1.0),需调整指数并重新归一化。
示例(续):
1.0 × 2⁰ + 0.1 × 2⁰ = 1.1 × 2⁰(无溢出)。
1.3、规格化(Normalization)
目标:确保结果尾数在 [1.0, 2.0) 范围内(隐含位为1)。
方法1:
若尾数结果≥2.0,左移尾数1位,指数加1。
若尾数结果<1.0,右移尾数1位,指数减1(可能需多次调整)。
方法2:
左规:尾数第一数值与符号位相同,左移一位,阶码减一。
右规:尾数01.xxxx或10.xxxx,尾数溢出,右移一位,阶码加一。
示例:
若结果为 0.11 × 2¹(非规格化),需右移尾数1位 → 1.10 × 2⁰,指数减1。
1.4、舍入(Rounding)
由于尾数位数有限,需对多余位进行舍入。IEEE 754提供四种模式:
1、向偶数舍入(Round to Nearest Even):默认模式,减少累积误差。
2、向零舍入(Truncate):直接截断低位。
3、向上舍入(Round Up):向正无穷方向舍入。
4、向下舍入(Round Down):向负无穷方向舍入。
示例:
若尾数结果为 1.01011(单精度需保留23位),第24位为1,且后续有非零位,则根据模式决定是否进位。
1.5、判断溢出
检查指数是否超出范围:
1、上溢:指数超过最大值(如单精度127),结果设为无穷大(±∞)。
阶码[j] 补 = 01,xxxx为上溢。
2、下溢:指数小于最小值(如单精度-126),结果设为0或非规格化数(Denormalized)。
阶码[j] 补 = 10,xxxx为下溢,按机器零处理。
1.6 、参考视频
实际考试中如何计算,参考以下视频:
浮点运算(浮点数加减运算)计算机组成原理(看了包会)
浮点数加减运算规格化(右规情况),阶码为负,溢出判断(计算机组成原理)
2、浮点数乘法运算
以下计算过程根据以下推导式设计:
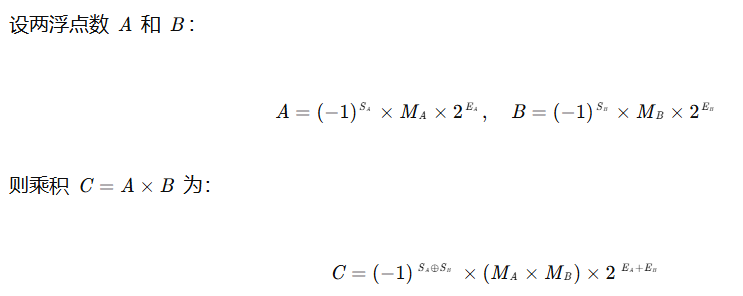
2.1、乘法运算步骤
2.1.1、符号位计算
规则:两数符号位异或(XOR)。
正 × 正 = 正(符号位 0)
负 × 负 = 正(符号位 0)
正 × 负 = 负(符号位 1)
2.1.2、 指数部分计算
规则:两数指数相加,再减去偏移量(单精度 127,双精度 1023)。
若结果指数超出范围(如单精度指数 > 254 或 < 1),需处理溢出或下溢。
示例:
1.5(指数 0) × 2.0(指数 1):
新指数 = 0+1−127=−126(存储为 −126+127=1)。
2.1.3、尾数部分计算
规则:两数尾数(含隐含的 1)相乘,结果需规格化:
1、相乘:将两数尾数(视为整数)相乘,得到一个新尾数。
2、规格化:
若结果 ≥ 2:右移 1 位,指数 +1。
若结果 < 1:左移若干位,指数 -相应值。
3、舍入:根据 IEEE 754 的舍入模式(如"就近舍入到偶数")处理多余位数。
示例:
1.5(尾数 1.1) × 2.0(尾数 1.0):尾数相乘:1.1 × 1.0 = 1.1(无需规格化)。结合指数调整后,结果为 3.0(二进制 1.1 × 2^1)。
2.2、参考视频推荐
3、浮点数除法运算
以下计算过程根据以下推导式设计:
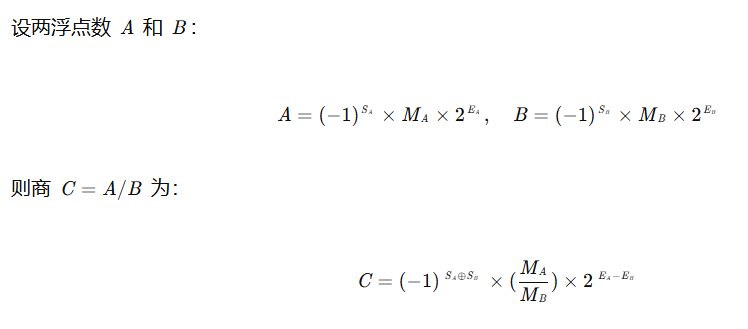
3.1.1、符号位计算
规则:两数符号位异或(XOR)。
正 × 正 = 正(符号位 0)
负 × 负 = 正(符号位 0)
正 × 负 = 负(符号位 1)
3.1.2、 指数部分计算
规则:被除数指数减去除数指数,再调整偏移量。
若结果指数超出范围(如单精度指数 > 254 或 < 1),需处理溢出或下溢。
数学表示:
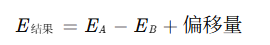
示例:
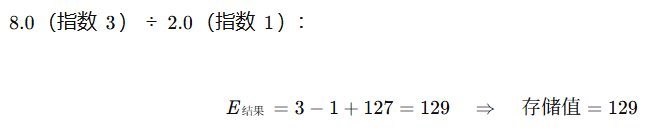
3.1.3、尾数部分计算
规则:被除数尾数(含隐含的 1)除以除数尾数,结果需规格化:
1、相除:将两数尾数(视为整数)相除,得到商和余数。

2、规格化:

3、舍入:根据 IEEE 754 的舍入模式(如"就近舍入到偶数")处理多余位数。
示例:
