
🔥小叶-duck:个人主页
❄️个人专栏:《Data-Structure-Learning》
《C++入门到进阶&自我学习过程记录》《算法题讲解指南》--从优选到贪心
✨未择之路,不须回头
已择之路,纵是荆棘遍野,亦作花海遨游
目录
09.长度最小的子数串
题目链接:
题目描述:

题目示例:

解法一:(暴力求解)(会超时)
算法思路:
【从前往后】枚举数组中的任意一个元素,把它当成起始位置。然后从这个【起始位置】开始,然后寻找一段最短的区间,使得这段区间的和【大于等于】目标值。
将所有元素作为起始位置所得的结果中,找到【最小值】即可。
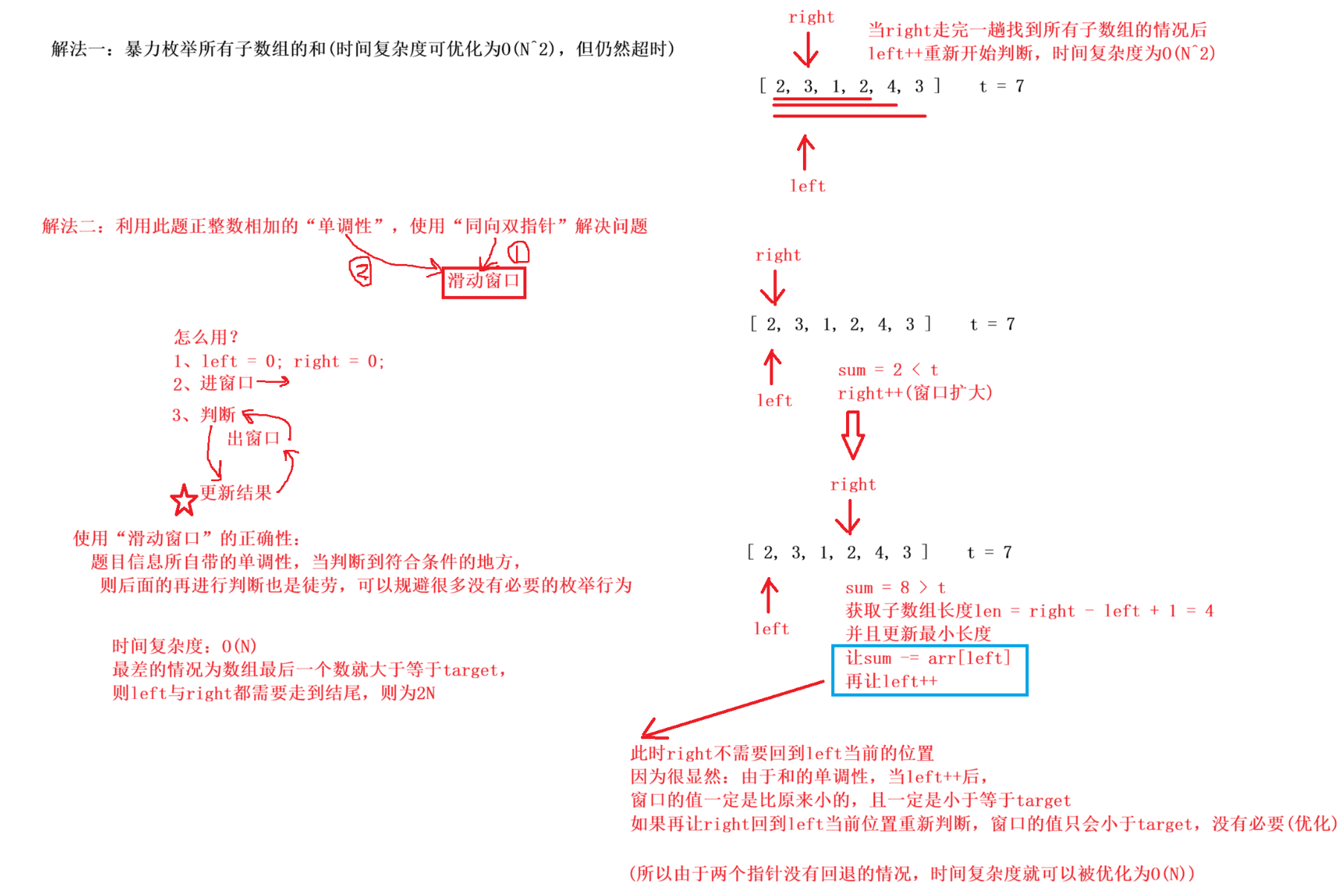
解法二:(滑动窗口)
算法思路:
由于此问题分析的对象是【一段连续的区间 】,因此可以考虑【滑动窗口】的思想来解决这道题。
让滑动窗口满足:从 i 位置开始,窗口内所有的和小于 target (那么当窗口内元素之和第一次大于等于目标值的时候,就是 i位置开始,满足条件的最小长度)。
做法:将右端元素划入窗口之中,统计出此时窗口内元素的和:
- 如果窗口内元素之和大于 target:更新结果,并且将左端元素划出去的同时继续判断是否满足条件并更新结果(因为左端元素可能很小,划出去之后依旧满足条件)
- 如果窗口内元素之和不满足条件:right++,另下一个元素进入窗口。
为何滑动窗口可以解决问题,并且时间复杂度更低?
这个窗口寻找的是:以当前窗口最左侧元素(记为left1 )为基准,符合条件的情况。也就是在这道题中,从 left1 开始,满足区间和 sum >= target 时的最右侧(记为 right1)能到哪里。
我们既然已经找到从 left1 开始的最优的区间,那么就可以大胆舍去left1 。但是如果继续像方法一一样,重新开始统计第二个元素(left2)往后的和,势必会有大量重复的计算(因为我们在求第一段区间的时候,已经算出很多元素的和了,这些和是可以在计算下次区间和的时候用上的)。
此时**,right1** 的作用就体现出来了,我们只需要将 left1 这个值从 sum 中剔除。从 right1 这个元素开始,往后找满足 left2 元素的区间 (此时 right1 也有可能是满足的,因为 left1 可能很小。sum 剔除掉 left1 之后,依旧满足大于等于 target)。这样我们就能省掉大量重复的计算。
时间复杂度:虽然代码是两层循环,但是我们的 left 指针和 right 指针都是不回退 的,两者最多都往后移动 n 次。因此时间复杂度是 O(N)。
C++代码演示:
cpp
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums)
{
// int left = 0;
// int right = -1;
// //right初始化为-1原因是target为正整数,一开始sum一定小于target
// //所以为了让right++并且能让sum能加上开头元素,就需要初始化为-1
// int len = 0;
// int n = nums.size();
// int min_len = n + 1; //先将最小长度置为非正常值,如果最后没有发生变化则说明没有符合条件的子数组
// int sum = 0;
// while (right < n)
// {
// if (sum >= target)
// {
// len = right - left + 1;
// if (min_len > len)
// {
// min_len = len;
// }
// sum -= nums[left];
// left++;
// }
// else
// {
// right++;
// if (right < n)
// {
// sum += nums[right];
// }
// else
// {
// break;
// }
// }
// }
// if(min_len == n + 1)
// {
// return 0;
// }
// return min_len;
//代码优化:
int n = nums.size();
int sum = 0;
int len = n + 1;
int left = 0;
int right = 0;
for(right = 0; right < n; right++)
{
sum += nums[right];//进窗口
while(sum >= target)//判断
{
len = min(len, right - left + 1);//更新结果
sum -= nums[left++];//出窗口
}
}
return len == n + 1 ? 0 : len;
}
};算法总结及流程解析:
10.无重复字符的最长字串
题目链接:
题目描述:
题目示例:

解法一:(暴力求解)(不会超时,可以通过)
算法思路:
枚举【从每一个位置】开始往后,无重复字符的子串可以到达什么位置。找到其中长度最大的即可。
在往后寻找无重复子串能到达的位置时,可以利用【哈希表 】统计出字符出现的频次,来判断什么时候子串出现了重复元素。
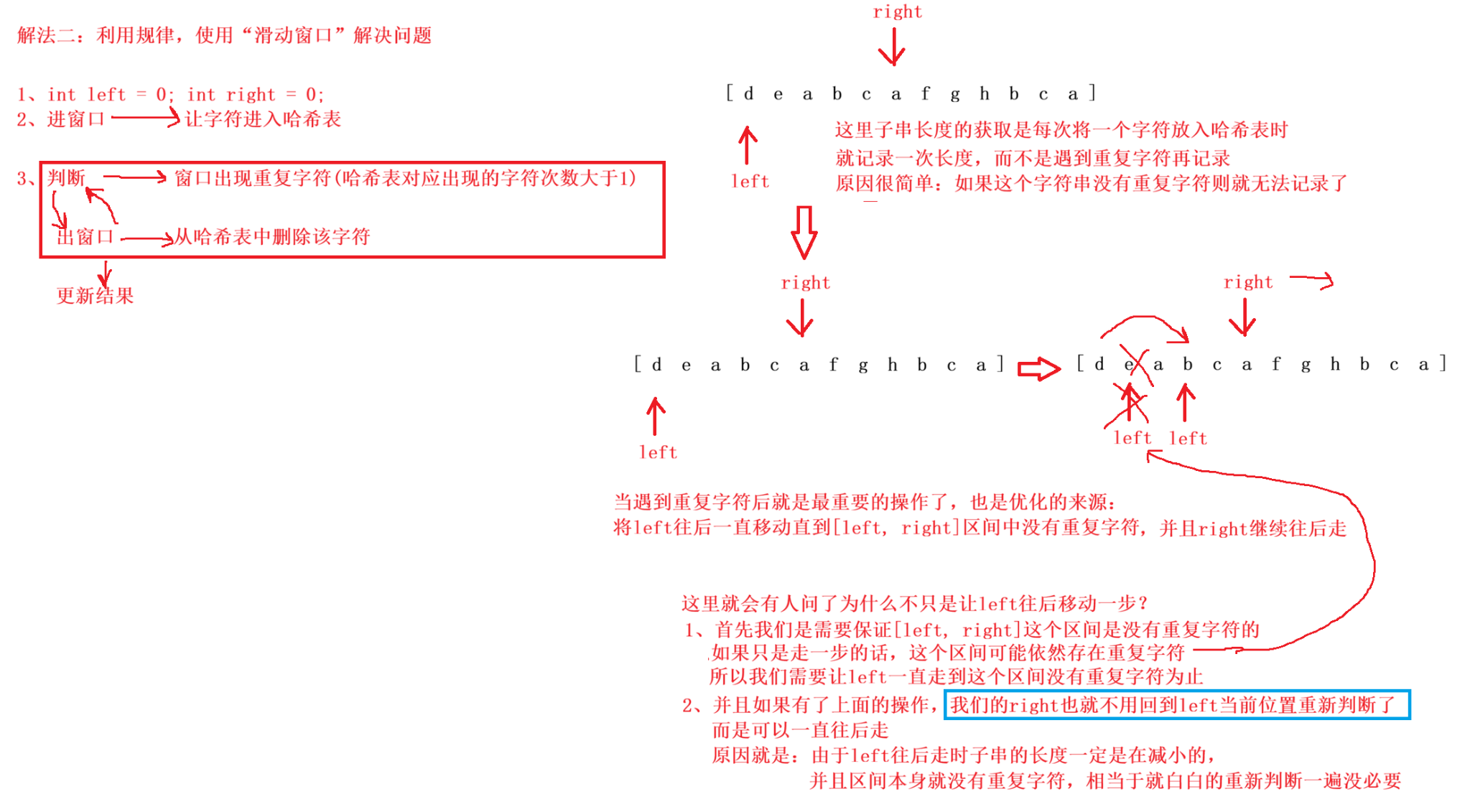
解法二:(滑动窗口)
算法思路:
研究的对象依旧是一段连续的区间 ,因此继续使用【滑动窗口】思想来优化。
让滑动窗口满足:窗口内所有元素都是不重复的。
做法:右端元素 s[ right ] 进入窗口的时候,哈希表统计这个字符的频次:
- 如果这个字符出现的频次超过 1 ,说明窗口内有重复元素 ,那么就从左侧开始划出窗口 ,直到 s[ right ] 这个元素的频次变为1,然后再更新结果。
- 如果没有超过 1,说明当前窗口没有重复元素,可以直接更新结果
C++代码演示:
cpp
class Solution {
public:
int lengthOfLongestSubstring(string s)
{
int len = 0;
int left = 0;
int right = 0;
int hash[128] = { 0 }; //使用数组来模拟哈希表
while(right < s.size())
{
hash[s[right]]++;//进入窗口
while(hash[s[right]] > 1)//判断
{
hash[s[left++]]--;//出窗口
}
len = max(len, right - left + 1);//更新结果
right++;
}
return len;
}
};算法总结及流程解析:

结束语
到此,09长度最小的子数串,10无重复字符的最长字串 两道算法题就讲解完了。**第一题,通过暴力解法和滑动窗口对比,详细解释了滑动窗口的高效原理,即通过左右指针不回退降低时间复杂度。第二题同样采用滑动窗口,利用哈希表统计字符频次来检测重复。**希望大家能有所收获!
