自创小算法00：数据分组

// 2026.02.21

对一堆数据nums进行组合，将分组的数据存入到s1和s2中，求解一共有多少种不同的分配方法，并将不同的分配方法保存到s1和s2中。

cc方法00：二进制枚举法

cpp 复制代码

#include <iostream>
#include <vector>
#include <algorithm>
#include <cassert>

using namespace std;

// ### 解决思路
// 1. 生成所有可能的子集组合：对于 `n` 个元素，共有 `2^n` 种分配方式（每个元素可以选择放入 `s1`组合 或 `s2`组合）。
// 2. 记录所有组合：将每种分配方式对应的 `s1` 和 `s2` 存入结果中。
// ### 实现方法
// 1. 位运算枚举：用整数 `mask` 的二进制位表示元素分配（二进制`1` 放入 `s1`，`0` 放入 `s2`）。
// 2. 动态构建子集：遍历 `mask`，根据二进制位动态生成 `s1` 和 `s2` 的当前组合。
// 3. 存储结果：将每个有效的 `s1` 和 `s2` 存入 `vector<vector<int>>` 中。
void calc(vector<int> nums, vector<vector<int>> &s1, vector<vector<int>> &s2)
{
    int n = nums.size();
    s1.clear();
    s2.clear();
    // 遍历所有可能的分配方式（2^n 种）- `1 << n` 是位运算，表示将数字1左移n位（即计算2的n次方）。
    // - 例如：当 `n=3` 时，`1<<3 = 8`，即共有8种分组方式。
    // 2. 遍历所有可能的掩码（mask）
    // for (int mask = 0; mask < sum; mask++)
    // - `mask` 是一个整数，其二进制形式用来表示当前的分组方案。
    // - 例如 `n=3` 时，`mask` 从 `000`（二进制）到 `111`（二进制），即0到7，一共8种。
    int sum = 1 << n;
    for (int mask = 0; mask < sum; mask++) {
        vector<int> cur1, cur2;
        // 根据 mask 分配数据，遍历每个bit，根据bit的值将对应的数据放入对应的组中
        // 检查对应nums中的每个数字对应的bit是否为1，如果为1则放入s1中，否则放入s2中
        for (int i = 0; i < n; i++) {
            // (1 << i)：生成一个只有第i位是1的数字
            // - `mask & (1 << i)`：检查 `mask` 的第i位是否是1。
            // - 若结果为真，则 `nums[i]` 放入 `s1`；否则放入 `s2`。
            if (mask & (1 << i)) {
                cur1.push_back(nums[i]); // 放入 s1
            } else {
                cur2.push_back(nums[i]); // 放入 s2
            }
        }
        // 存储当前组合
        s1.push_back(cur1);
        s2.push_back(cur2);
    }
}

int main()
{
    int n = 0;
    while (cin >> n) {
        vector<int> nums(n, 0);
        vector<vector<int>> s1, s2;
        for (int i = 0; i < n; ++i) {
            cin >> nums[i];
        }
        calc(nums, s1, s2);
        if (s1.size() != s2.size()) {
            cout << "error : s1.size() != s2.size()" << endl;
            assert(0);
        }
        // 输出所有组合
        for (int i = 0; i < s1.size(); i++) {
            cout << "Combination " << i + 1 << ":" << endl;
            cout << "s1: ";
            for (int num : s1[i]) cout << num << " ";
            cout << endl << "s2: ";
            for (int num : s2[i]) cout << num << " ";
            cout << endl << "----------------------" << endl;
        }
    }

    return 0;
}

cc方法0：二进制枚举法优化

cpp 复制代码

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

// 用于存储一堆数据分成两组时每个组中间的数字
using myType = pair<vector<int>, vector<int>>;

vector<myType> GetRes(const vector<int> & nums)
{
    vector<myType> res;
    int n = nums.size();
    int sum = 1 << n;
    for (int mask = 0; mask < sum; ++mask) {
        vector<int> s1;
        vector<int> s2;
        for (int i = 0; i < n; ++i) {
            if (mask & (1 << i)) {
                s1.push_back(nums[i]);
            } else {
                s2.push_back(nums[i]);
            }
        }
        res.push_back({s1, s2});
    }

    return res;
}

int main()
{
    int n = 0;
    while (cin >> n) {
        vector<int> nums(n, 0);
        for (int i = 0; i < n; ++i) {
            cin >> nums[i];
        }
        vector<myType> res = GetRes(nums);
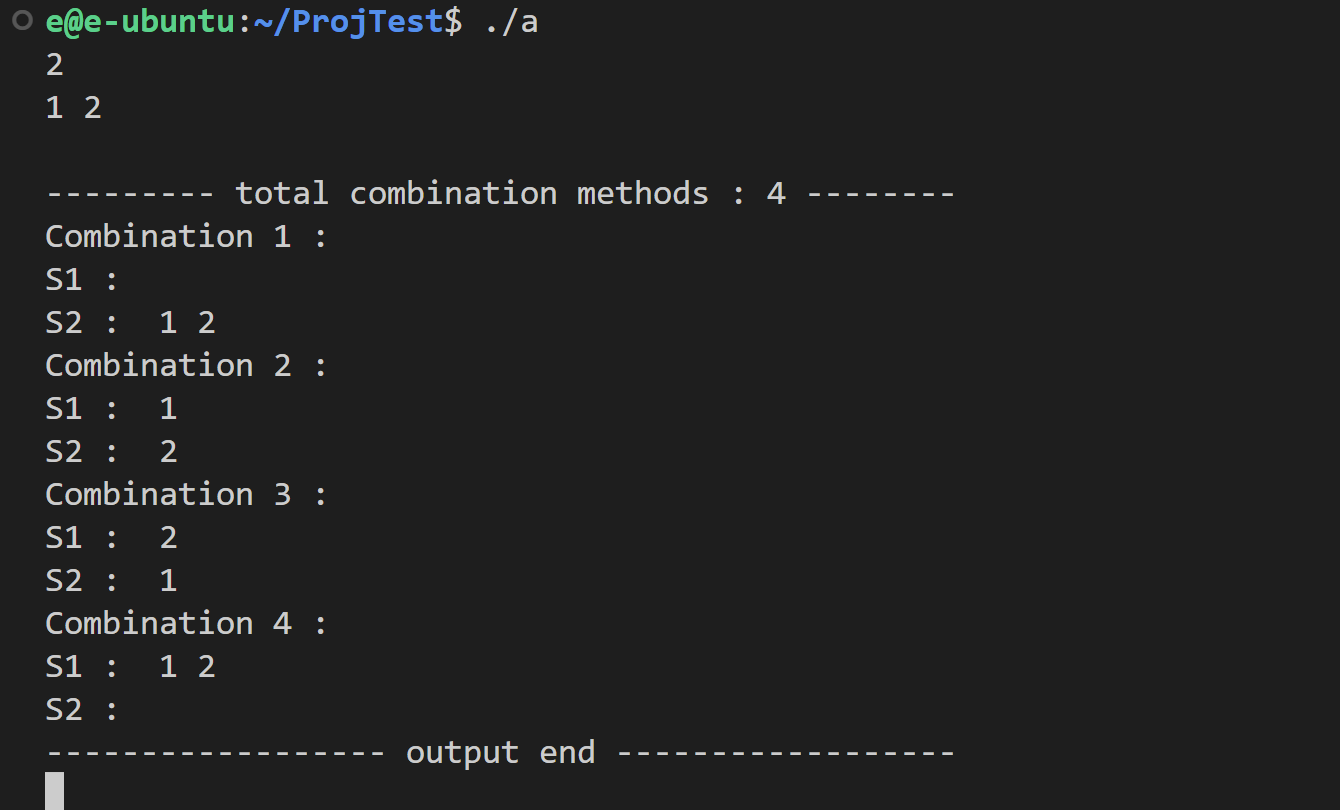
        // 输出所有组合数
        cout << endl << "--------- total combination methods : " << res.size() << " --------";
        for (int i = 0; i < res.size(); ++i) {
            cout  << endl << "Combination " << i + 1 << " :" << endl;
            cout << "S1 : ";
            for (const int n : res[i].first) {
                cout << " " << n;
            }
            cout << endl << "S2 : ";
            for (const int n : res[i].second) {
                cout << " " << n;
            }
        }
        cout << endl << "------------------ output end ------------------" << endl;
    }

    return 0;
}

// 输入输出示例：