0.位运算基础
在看具体的题目之前,需要先了解一些常见的位运算操作。
(1)运算符
<<左移
>>右移
&按位与:有0则为0
|按位或:有1则为1
^按位异或:相同为0,相异为1
(2)具体操作
①给定一个数n,确定它的二进制表示中的第x位是0还是1
(n>>x)&1
x x x x x x x x->0 0 0 0 0 0 0 ?(若原位为0,则得到的数为0,若原位为1,则得到的数为1)
②将一个数n的二进制表示的第x位修改成1
n|=(1<<x)
③将一个数n的二进制表示的第x位修改成0
n&=(~(1<<x))
④位图的思想
用32位二进制数每一位中的0或1来表示信息
⑤提取一个数n二进制表示中最右侧的1
n&(-n)
意思是:
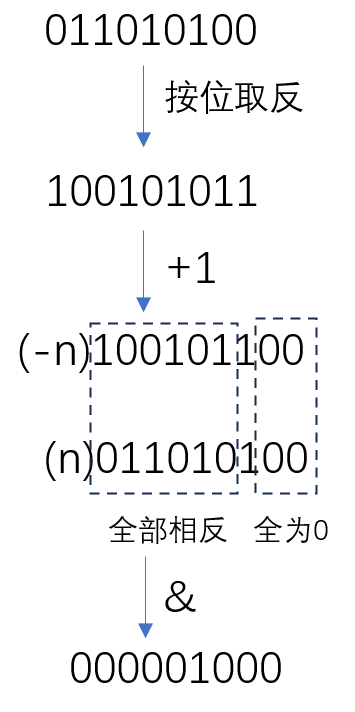
⑥将一个数n二进制表示中最右侧的1变成0
n&(n-1)
意思是: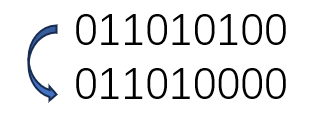

⑦异或(^)运算的运算律
a^0=a
a^a=0
a^b^c=a^(b^c)
1.判定字符是否唯一
面试题 01.01. 判定字符是否唯一 - 力扣(LeetCode)

用位图的思想去做,每一位的1或0代表字符已经存在或否
但这其实也有局限性,一个int只有32个二进制位,这里的字符刚好只包括小写字母,如果是更多可能就不适用了。
进入循环先判断该字符在位图中的位置是0还是1,是1则表示已经存在过了,直接false,是0则存入。另外还有一个优化:根据鸽巢原理,原字符串长度如果超过26则一定有重复,可以提前判断一下。
代码如下:
cpp
class Solution
{
public:
bool isUnique(string astr)
{
if(astr.size()>26)
{
return false;
}
int bitMap=0;
for(int i=0;i<astr.size();i++)
{
int n=astr[i]-'a';
if(((bitMap>>n)&1)==0)
{
bitMap|=(1<<n);
}
else
return false;
}
return true;
}
};2.丢失的数字
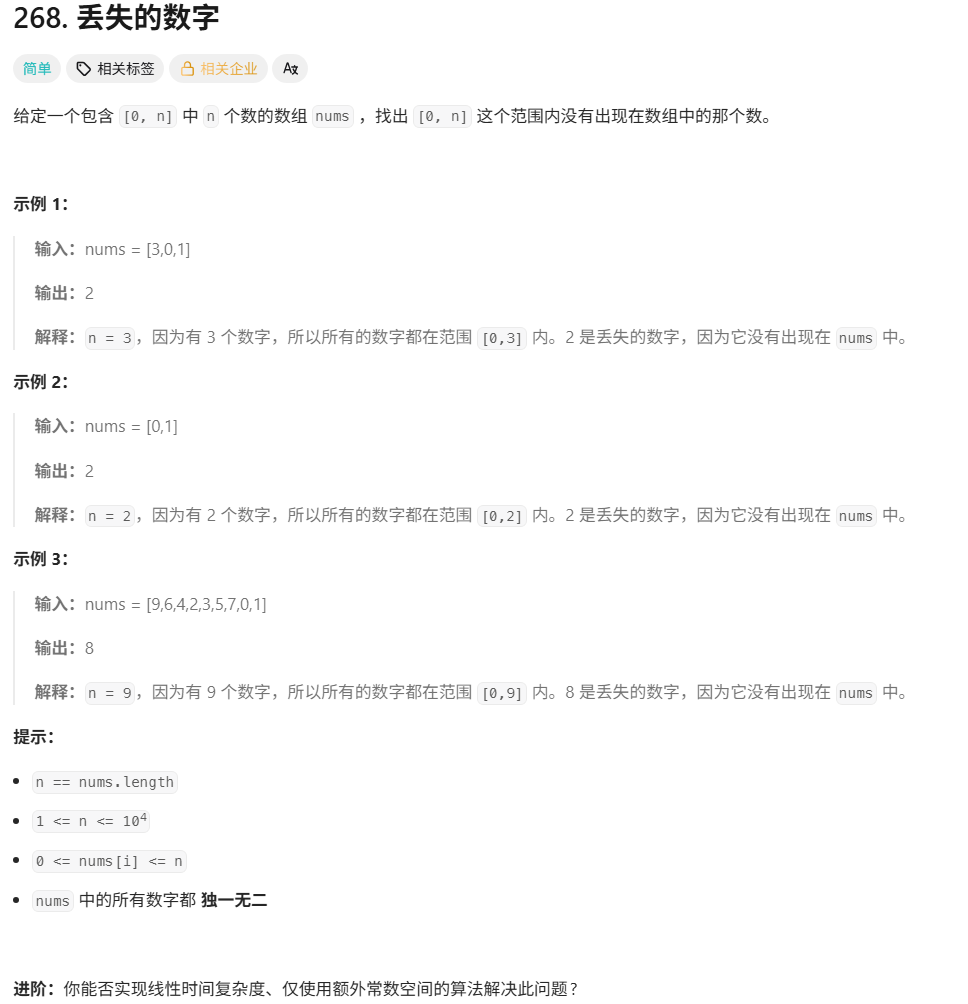
方法有很多:
①用哈希表储存字符出现的次数
②高斯求和 Sn-sum[nums]
③位运算 创建一个不缺失的数组(不用真的创建,遍历的i就可以当作数组元素),和nums中的所有元素全部异或起来,得到的值就是缺失的数字
代码如下:
cpp
class Solution {
public:
int missingNumber(vector<int>& nums)
{
int n=nums.size(),ret=0;
for(int i=0;i<n;i++)
{
ret^=nums[i];
ret^=i;
}
ret^=n;
return ret;
}
};3.两整数之和

这种不允许用运算符的题可以考虑一下位运算
用异或解决(因为异或是无进位相加,只要找到进位即可)
只有1+1会产生进位,所以凡有0的进位都是0,用&
示例:13+28=41

代码如下:
cpp
class Solution {
public:
int getSum(int a, int b)
{
int ret=0;
unsigned int n=0;
while(b)
{
ret=a^b;
n=(unsigned int)(a&b)<<1;
a=ret;
b=n;
}
return a;
}
};4.只出现一次的数字Ⅱ
137. 只出现一次的数字 II - 力扣(LeetCode)

对于二进制表示的每一位,如果将数组所有元素相加起来,有且仅有4种情况:
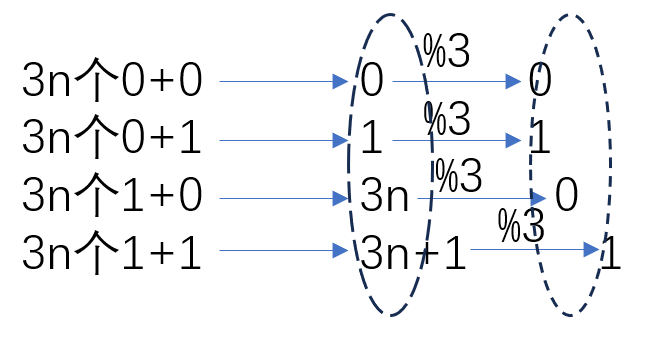
可见,处理后的数位和要找的数的数位是一一对应的,所以可以循环遍历32个数位,将处理后的数填充到其中即可
代码如下:
cpp
class Solution {
public:
int singleNumber(vector<int>& nums)
{
int ret=0;
for(int i=0;i<32;i++)
{
int sum=0;
for(auto x:nums)
{
if(((x>>i)&1))
{
sum++;
}
}
sum%=3;
if(sum)
{
ret|=(1<<i);
}
}
return ret;
}
};5.消失的两个数字
面试题 17.19. 消失的两个数字 - 力扣(LeetCode)

将不缺失的数组中的元素和题给数组中的元素异或在一起,最终得到的tmp是缺失的a和b异或的结果,由于异或相异为1,找到tmp的二进制表示中为1的位下标(其中一个),可知它是由该位上a和b的0和1异或而成的,根据该位为0或1,可以将其余所有元素分为两类,这两类分别异或可以分别得到a和b
代码如下:
cpp
class Solution {
public:
vector<int> missingTwo(vector<int>& nums)
{
int tmp=0,b=0,a=0;
int n=nums.size();
for(int i=1;i<=n+2;i++)tmp^=i;
for(auto x:nums) tmp^=x;
int diff=0;
for(;diff<32;diff++)
{
if(((tmp>>diff)&1)) break;
}
for(int i=1;i<=n+2;i++)
{
if(((i>>diff)&1)) a^=i;
else b^=i;
}
for(auto x:nums)
{
if(((x>>diff)&1)) a^=x;
else b^=x;
}
return{a,b};
}
};