【KMP】算法详解

前言

本文将详细讲解 KMP (看毛片) 算法.

例题引入

首先我们来看一道题目:

题目描述

给定两个字符串 A A A 和 B B B,

输出字符串 B B B 在字符串 A A A 的每一个出现的位置
输入样例
复制代码
aabcabc
abc
输出样例
复制代码
2
5
容易发现，字符串 aabcabc 中有两个子串 abc，开头位置为 2 2 2 和 5 5 5.
数据规模

设 ∣ S ∣ |S| ∣S∣ 表示字符串 S S S 的长度
1 ≤ ∣ A ∣ , ∣ B ∣ ≤ 1.1 × 10 7 1\leq |A|,|B| \leq1.1\times10^7 1≤∣A∣,∣B∣≤1.1×107

什么? ∣ A ∣ , ∣ B ∣ ≤ 1.1 × 10 7 |A|,|B| \leq 1.1\times10^7 ∣A∣,∣B∣≤1.1×107，这么大的数据意味着我们必须考虑 O ( ∣ A ∣ + ∣ B ∣ ) O(|A| + |B|) O(∣A∣+∣B∣) 的算法.

但是我们发现我们想不出来（你又不是 Knuth-Morris-Pratt 这 3 位大佬），所以我们必须一步一个脚印，不断优化暴力.

比暴力还暴力的暴力

根据骗分大佬的影响，我们一定要坚信以下的口诀：

骗分过样例，暴力出奇迹。打表进省一，口诀要牢记。

所以，我们直接设计一个 O ( ∣ A ∣ ∣ B ∣ ) O(|A||B|) O(∣A∣∣B∣) 的算法，直接暴力匹配每一位.

以图片说明精髓

不要小看这个算法，这个和我们接下来的算法有很大的联系.

下面将给出图片，手模样例来说明这个比暴力还暴力的暴力 的算法.

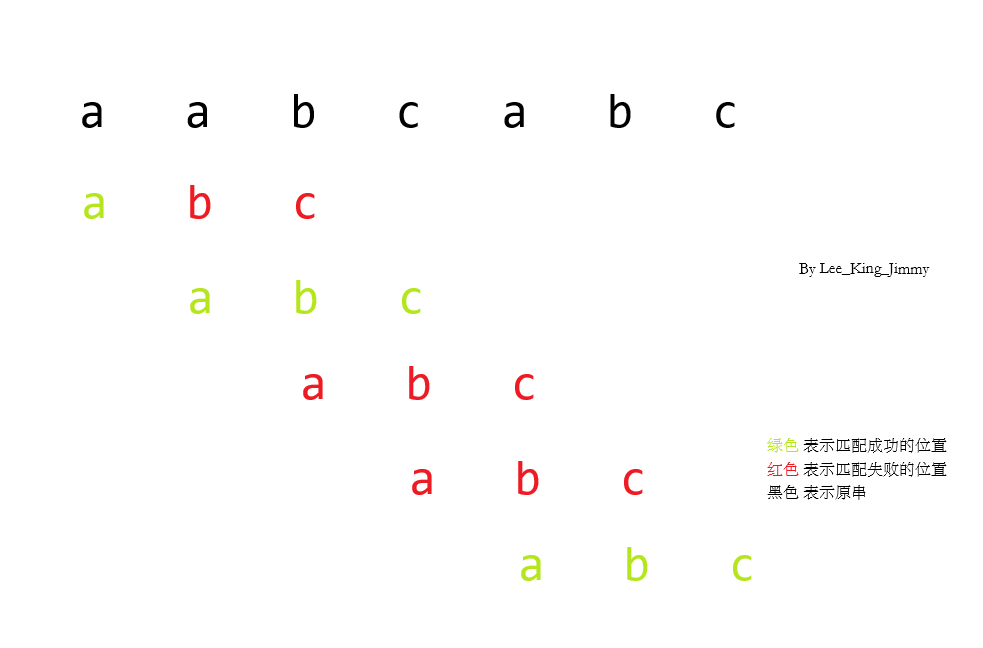
容易发现，这个算法就是将串 abc 和串 aabcabc 进行匹配，然后发现匹配成功有两个位置.

代码彰显思维

cpp 复制代码

#include <stdio.h>
#include <string.h>

void bruteForceSearch(char text[], char pattern[]) {
    int n = strlen(text);
    int m = strlen(pattern);
    
    for (int i = 0; i <= n - m; i++) {
    	int ok_pos = 0;		// 相等的个数
        for (int j = 0; j < m; j++)
            if (text[i + j] == pattern[j])			// 如果两个位置相等，那么相等的个数++
                ok_pos++;
       	if (ok_pos == m) printf("%d\n", i);		/// 如果匹配的位置达到 m 个，那么代表这个位置是可以匹配的
    }
}

强大的暴力取得了显著的效果.

没有暴力那么暴力的暴力

我们可以发现一个优化，上面的算法将每一个位置都进行了暴力，那么我们可以进行一个简单的优化: 只要有一个位置不匹配，我们就直接跳出，下面给出图.

震惊！令人震惊的结果！

数据太水了！直接卡过了！！！！！！！！！！！！

果然，一个小小的优化就水过去了 (因为这个题目的 ∣ A ∣ ≤ 10 5 |A|\leq10^5 ∣A∣≤105，强行卡过去了！)

代码

cpp 复制代码

#include <stdio.h>
#include <string.h>

void bruteForceSearch(char text[], char pattern[]) {
	int n = strlen(text);
	int m = strlen(pattern);
	
	for (int i = 0; i <= n - m; i++) {
		int j = 0;		// 相等的个数
		for (; j < m; j++)
			if (text[i + j] != pattern[j])			// 如果两个位置不相等，那么匹配没有意义，直接跳出即可
				break;
		if (j == m) printf("%d\n", i + 1);		/// 如果匹配的位置达到 m 个，那么代表这个位置是可以匹配的
	}
}

const int MAXN = 100010;
char str1[MAXN], str2[MAXN];
int main() {
	int N, M;
	scanf("%d%d%s%s", &N, &M, str1, str2);
	bruteForceSearch(str1, str2);
}

正题 --- KMP 匹配算法

我们发现暴力属实还是没有那么靠谱，那么我们现在请出 O ( ∣ A ∣ + ∣ B ∣ ) O(|A| + |B|) O(∣A∣+∣B∣) 复杂度的 K M P KMP KMP 算法.

细节

现在我们将前面的暴力算法放慢速度，一步一步来看。

首先如果我们不知道 上面的串 A A A(下面称其为 模板串 )，再看一张图:

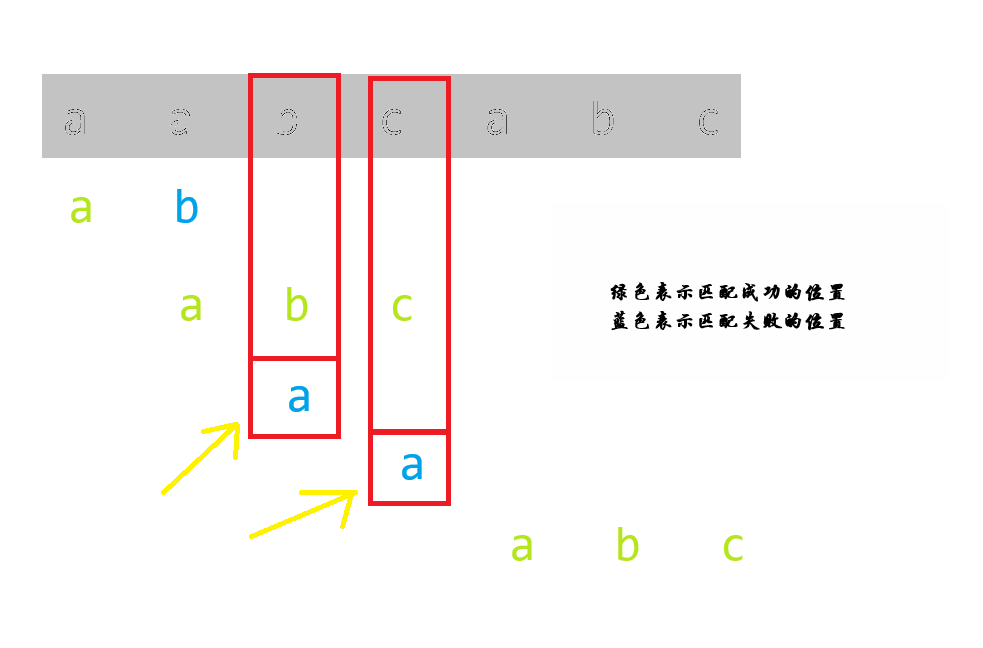
（图片略微有点丑）

然后我们观察第一次匹配成功的位置，也就是第二次匹配的位置 (图片上面第一个绿色的 abc).

重点来了

我们发现黄色箭头所指向的位置，标记为蓝色的两个 a，是完全没有必要匹配的，换句话说，就是匹配一定会产生错误的位置.

为什么 (建议读者详细理解这个简单道理，这至关重要)

容易发现，前面 B B B 串已经匹配成功了一次!，换句话说，就是两个 a 头顶上面的位置一定是字符 b 和 c!

所以，这种一定会失败的匹配就不要匹配了！

这个小小的细节就是 kmp 比其他算法的高明之处。

上面启示我们 "只看串 B",使用程序实现就是要对串 B B B 进行一个预处理 ，然后根据这个串的某一种性质去跳过一些不可能的匹配.

如此简单的道理，需要理解吗?(作者理解了半天)
如果没有理解上面这个简单的道理，那就一定要回头看，不然你会学不下去的

最长公共前后缀(失配函数)

（主菜要上桌了！！！！！！！！！）

不要被标题吓到，其实我们前面已经接触和好几个积性函数 -- 刘汝佳《算法竞赛入门经典-训练指南》

这个东西又不是积性函数，怕什么!

定义

抽象定义(密集恐惧症者请远离)

给定一个长度为 𝑛 𝑛 n 的字符串 s s s，其 前缀函数 被定义为一个长度为 n n n 的数组 π \pi π 其中 π [ i ] \pi[i] π[i] 的定义是：

s [ 0 ... i ] s[0\dots i] s[0...i] 有一对相等的真前缀与真后缀： s [ 0 ... k − 1 ] s[0\dots k-1] s[0...k−1] 和 s [ i − ( k − 1 ) ... i ] s[i - (k - 1) \dots i] s[i−(k−1)...i]，那么 π [ i ] \pi[i] π[i] 就是这个相等的真前缀（或者真后缀，因为它们相等）的长度，也就是 π [ i ] = k \pi[i]=k π[i]=k；

如果不止有一对相等的，那么 π [ i ] \pi[i] π[i] 就是其中最长的那一对的长度；

如果没有相等的，那么 π [ i ] = 0 \pi[i]=0 π[i]=0．

-- from oi-wiki

说人话就是：字符串含有的最长公共前后缀的长度 (废话)

举例子

考虑字符串 aabcaabc.

i = 0 i=0 i=0，字符串为 a，最长公共前后缀为 0 0 0(注意这里前后缀不能重复)
i = 1 i=1 i=1, 字符串为 aa, π [ i ] = 1 \pi[i]=1 π[i]=1. (前缀为 a, 后缀为 a, 相等，长度为 1 1 1)
i = 2 i=2 i=2, 字符串为 aab, π [ i ] = 0 \pi[i]=0 π[i]=0.
i = 3 i=3 i=3, 字符串为 aabc, π [ i ] = 0 \pi[i]=0 π[i]=0.
i = 4 i=4 i=4, 字符串为 aabca, π [ i ] = 1 \pi[i]=1 π[i]=1 (最长公共前后缀为 a).
i = 5 i=5 i=5, aabcaa， π [ i ] = 2 \pi[i]=2 π[i]=2(为 aa).
...
i = 7 i=7 i=7，就是原串， π [ i ] = 4 \pi[i]=4 π[i]=4(为 aabc).

计算方法

这里我们直接考虑 O ( N ) O(N) O(N) 计算前缀函数。

我们考虑使用 动态规划 解决这个问题。

假设我们现在已经求出了 π [ 0 ... i − 1 ] \pi[0 \dots i-1] π[0...i−1]，现在我们要求出 π [ i ] \pi[i] π[i].

Part 1:

根据假设，我们现在知道了 π [ i − 1 ] \pi[i-1] π[i−1]，这代表着什么？

代表着 A [ 0 ... π [ i − 1 ] − 1 ] = A [ i − π [ i − 1 ] ... i − 1 ] (前缀函数的定义) A[0 \dots \pi[i-1]-1]=A[i-\pi[i-1] \dots i-1]\tag{前缀函数的定义} A[0...π[i−1]−1]=A[i−π[i−1]...i−1](前缀函数的定义)

这个很好理解，就是这个函数的定义。

对上面的举例子

首先我们考虑字符串 aaabc,

当 i = 2 i=2 i=2 时，前缀函数 π [ i ] = 1 \pi[i]=1 π[i]=1 (为 a) .

然后我们发现, A [ 0 ... π [ i − 1 ] − 1 ] = A [ i − π [ i − 1 ] ... i − 1 ] A[0 \dots \pi[i-1]-1]=A[i-\pi[i-1] \dots i-1] A[0...π[i−1]−1]=A[i−π[i−1]...i−1]

代入 π [ i ] = 1 \pi[i]=1 π[i]=1 得: A [ 0 ... 0 ] = A [ 1 ... 1 ] A[0 \dots 0]=A[1\dots1] A[0...0]=A[1...1]

就是 A A A 中的字符 a, 他们相等

下面我们分情况进行讨论：

如果 A [ π [ i − 1 ] ] = A [ i ] A[\pi[i-1]]=A[i] A[π[i−1]]=A[i]

这就意味着，当前这个位置形成了长度为 π [ i − 1 ] + 1 \pi[i-1]+1 π[i−1]+1 的串.
为什么？ （下面高能，如果没有理解就一定要再看一看，这是最难理解的部分）

回顾我们之前的条件， A [ 0 ... π [ i − 1 ] − 1 ] = A [ i − π [ i − 1 ] ... i − 1 ] A[0 \dots \pi[i-1]-1]=A[i-\pi[i-1] \dots i-1] A[0...π[i−1]−1]=A[i−π[i−1]...i−1]

那么现在多了 A [ π [ i − 1 ] ] = A [ i ] A[\pi[i-1]]=A[i] A[π[i−1]]=A[i]

是不是就意味着 A [ 0 ... π [ i − 1 ] ] = A [ i − π [ i − 1 ] ... i ] A[0 \dots \pi[i-1]]=A[i-\pi[i-1] \dots i] A[0...π[i−1]]=A[i−π[i−1]...i]

很容易可以知道，这里的长度为 π [ i − 1 ] + 1 \pi[i-1]+1 π[i−1]+1，所以当前失配函数的值就是 π [ i ] = π [ i − 1 ] + 1 \pi[i]=\pi[i-1]+1 π[i]=π[i−1]+1

你如果不理解，就再看看上面的推导，我相信只要是有小学四年级的水平的读者，都是可以看懂的.
(你如果真的不懂，那么就再看1次，或者在评论区提问)

第二种情况的讨论就比较复杂了，写在下面的部分

Part 2:
主菜中最好吃的部分到了

现在我们来解决，如果 A [ π [ i − 1 ] ] ≠ A [ i ] A[\pi[i-1]]\neq A[i] A[π[i−1]]=A[i]

根据前面第一部分的启发，我们现在的目标就是

找到一个更短的 π [ k ] \pi[k] π[k]，使得 A [ π [ k ] ] = A [ i ] A[\pi[k]]=A[i] A[π[k]]=A[i]，那么循环节的长度就是 k + 1 k+1 k+1，即 π [ i ] = k + 1 \pi[i]=k+1 π[i]=k+1.

换而言之，我们要继续沿着失配函数跳，直到这个条件成立.

具体而言，这个过程可以这样理解

我们考虑 "跳"

Part 1:

我们令 j = π [ i − 1 ] j=\pi[i-1] j=π[i−1]，那么可能最短的最长公共前后缀就是 π [ j − 1 ] \pi[j-1] π[j−1].

这个东西非常容易理解，我们知道，现在要得到一个 π [ k ] \pi[k] π[k]，然后要使 k + 1 k+1 k+1 最大(因为要取最长的公共前后缀).

所以这个自然是最好的选择。

为什么这个不会丢失答案 。就是为什么前面的 dp 是正确的？

因为我们知道，相邻的前缀函数要么增加 1 1 1，要么为 0 0 0.

这个是很好理解的，所以上面是正确的，具体可以查看 OI_WIKI.
然后我们在计算 π [ j − 1 ] \pi[j-1] π[j−1] 时，可以按照我们上面对 i i i 的讨论，分成相等和不相等，本质上就是一个递归的过程.

代码

下面将给出代码，代码中不同的地方就是 π [ i ] \pi[i] π[i] 指的是上面的 π [ i − 1 ] \pi[i-1] π[i−1] 的值，就是 π [ i ] \pi[i] π[i] 表示的是 A [ 0 ... i − 1 ] A[0 \dots i-1] A[0...i−1] 而不是 A [ 0 ... i ] A[0 \dots i] A[0...i]，这样给计算带来了方便.

cpp 复制代码

// 计算失配函数 f
int f[MAXN];		// 最长公共前后缀
char s2[MAXN];	// 字符串
void GetFail() {
	f[0] = f[1] = 0;		// 这是显然的, 
	for (int i = 1; i < M; i++) {
		int j = f[i];		// 这里初始化 j
		while (j && s2[i] != s2[j]) j = f[j];		
		/*这里就是主过程，也就是不断递归下去计算, 也就是某些文献当中的 "沿着失配边跳".*/
		f[i + 1] = (s2[i] == s2[j]) ? j + 1 : 0;
		/*这里按照上面的更新值，注意 f[i+1] 其实就是上面的 pi[i], 下标集体后移了 1 位*/
	}
}

然后这个代码的时间复杂度是 O ( N ) O(N) O(N) 的，证明略。

提示:

在其他大佬的博客里面写的代码，可以没有 while 循环。

因为我上面的代码其实是 MP 算法，但是 KMP 算法就是进一步优化了常数，去掉了内部的循环

但是这个东西包含了一些有用的性质，所以建议初学者学习这一份代码.

一定要理解上面的算法，这个是最难理解的部分

说明

可能有读者会抱怨没有图片，但是上面的部分用图片并不好说明，如果出现自己的见解，我们评论区讨论

匹配过程

相较于上面的前缀函数，这部分可能会简单一些.

这里我们通过两个游标实现.

i i i 表示字符串 A A A 匹配到了第几位.
j j j 表示字符串 B B B 匹配到了第几位.

现在我们来模拟一下匹配的过程：

我们假设 A = " a a b a c a a a b a a " , B = " a a b a a " A="aabacaaabaa",B="aabaa" A="aabacaaabaa",B="aabaa".

第一个位置相等，此时 i++,j++.

变成 i = j = 2 i=j=2 i=j=2 就是匹配到第二个位置.

发现第二个位置也相等，我们直接 i++, j++.

现在 i = 3 , j = 3 i=3, j=3 i=3,j=3。

依旧相等，那么 i++, j++.

现在 i = 4 , j = 4 i=4, j=4 i=4,j=4。

还是相等，现在 i = j = 5 i=j=5 i=j=5.

出现不相等的情况，那么我们怎么办？

按照原来暴力算法的思路，那么我们是要将后面这个字符串移动一位的，但是我们觉得这样子太笨了。

我们直接通过之前学习到的失配函数 π \pi π, 不难发现 π [ 5 − 1 ] = π [ 4 ] = 1 , 1 + 1 = 2 \pi[5-1]=\pi[4]=1, 1+1=2 π[5−1]=π[4]=1,1+1=2，那么我们跳到位置 2 2 2 去匹配。

也就是将字符 c 和字符 a(第二个 a), 去匹配.

为什么

因为我们知道，最长公共前后缀就是前缀和后缀相等 ，在这个例子当中，也就是字符 a(第一个) 和字符 a(第 4 个) 相等.

然后我们可以直接将第一个位置移动到第 4 4 4 个位置进行匹配（暴力算法是后移一位到位置 2 2 2），不难发现，因为他们是相等的条件，那么这个匹配一定就是成功的 .

所以我们将刚才的第 2 2 2 个字符 a 和字符 c 匹配即可。

仔细想一想，我们就可以发现，后面的位置一定是行不通的(这个问题留给读者自己进行模拟)。

还是匹配失败，怎么办？

我们就按照刚才的方法继续跳，跳到 j = π [ 2 − 1 ] = π [ 1 ] = 0 j=\pi[2-1]=\pi[1]=0 j=π[2−1]=π[1]=0，好了，现在 j = 0 j=0 j=0, 那么就无法匹配了，就要换到下一个位置重新开始。

下面就不给出图片了，相信读者一定是可以做到模拟出这个算法的。

刚才 "跳" 和前面的预处理失配函数很类似，这里就直接给出详细的代码：

代码

cpp 复制代码

void KMP() {
	int j = 0;
	for (int i = 0; i < N; i++) {
		while (j && s1[i] != s2[j]) j = f[j];
		if (s1[i] == s2[j]) j++;
		if (j == M) printf("%d\n", i - M + 2);
	}
}

完整代码

cpp 复制代码

#include <iostream>

using namespace std;
int N, M;

const int MAXN = 1e6 + 10;

char s1[MAXN], s2[MAXN];

// 计算失配函数 f
int f[MAXN];		// 最长公共前后缀
void GetFail() {
	f[0] = f[1] = 0;		// 这是显然的, 
	for (int i = 1; i < M; i++) {
		int j = f[i];
		// cout << j << endl;
		while (j && s2[i] != s2[j]) j = f[j];
		f[i + 1] = (s2[i] == s2[j]) ? j + 1 : 0;
	}
}

void KMP() {
	int j = 0;
	for (int i = 0; i < N; i++) {
		while (j && s1[i] != s2[j]) j = f[j];
		if (s1[i] == s2[j]) j++;
		if (j == M) printf("%d\n", i - M + 2);
	}
}

int main()
{
	// freopen("a0.in", "r", stdin);
	cin >> N >> M;
	cin >> s1 >> s2;
	
	// cout << "START" << endl;
	GetFail();
	// cout << "OK" << endl;
	KMP();

	return 0;
}

这是完整代码，仅仅使用 3 m s 3ms 3ms.

写在最后

字符串算法真的很重要，所以建议大家多做题，如果还没有理解这个算法，可以再看一次，也可以在评论区讨论。

一些题目： link

提示

这个网站是一个很好的网站，推荐给大家，如果不懂的也可以看看！

给个三连吧！