回溯算法 -- 216. 组合总和 III

一.题目描述

二.解题思路

三.回溯三部曲

3.1确定递归函数的参数

3.2确认递归的终止条件

3.3确定单层循环逻辑

四.具体的代码

一.题目描述

找出所有相加之和为 n的 k个数的组合，且满足下列条件：

只使用数字1到9
每个数字 最多使用一次

返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例 1:

复制代码

输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。

示例 2:

复制代码

输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。

示例 3:

复制代码

输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字，我们可以得到的最小和是1+2+3+4 = 10，因为10 > 1，没有有效的组合。

二.解题思路

本题我们可以采用回溯算法的思想来解决这个问题

回溯算法的核心是我们要将其转换为树形结构

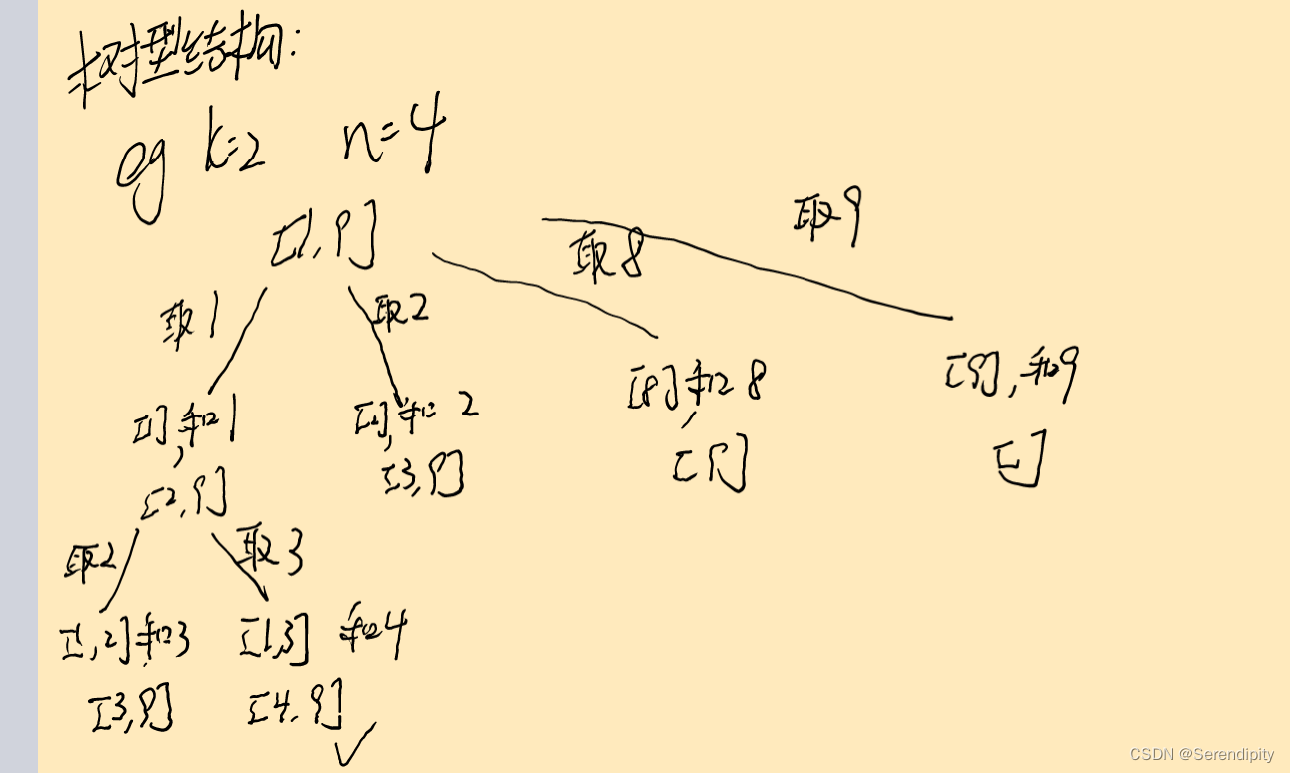
三.回溯三部曲

3.1确定递归函数的参数

java 复制代码

 List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();

此处我定义了一维数组path来存放符合条件的结果

定义二维数组result来存放结果集

除了这两个全局变量外,我们还需要以下参数:

targetSum(int) 目标和对应的就是题目中给出的n。

k(int) 这个为题目中给出的k个数的集合。

sum(int) 计算已经收集的元素的总和,也就是我们上面定义的path数组里元素的。

startIndex(index) 为下一层for循环的起始位置。

3.2确认递归的终止条件

本题的终止条件由两部分组成

path数组中的元素和达到题目中给出的n

path数组的长度达到题目中给出的k

java 复制代码

 //确定终止条件
        //目标数组长度达到k,且之和为n
        if(path.size() == k && sum == targetSum){
            result.add(new ArrayList<>(path));
            return;
        }

3.3确定单层循环逻辑

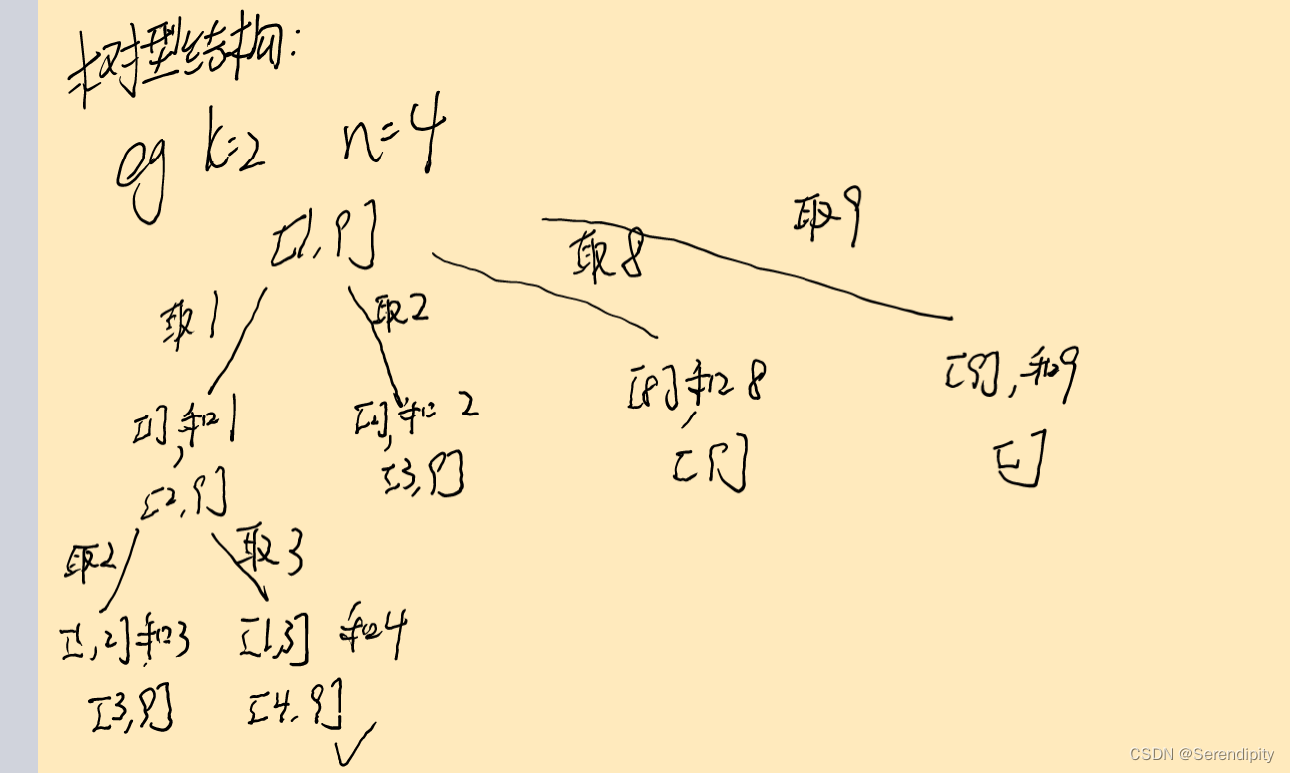
处理过程就是 path收集每次选取的元素，相当于树型结构里的边，sum来统计path里元素的总和。

java 复制代码

 for (int i = startIndex; i <= 9-(k-path.size())+1 ; i++) {
            //处理节点
            path.add(i);
            sum+=i;
            //递归函数
            backtracking(k,targetSum,i+1,sum);
            //回溯操作
            sum-=i;
            path.removeLast();
        }

四.具体的代码

java 复制代码

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;

public class Solution216 {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combinationSum3(int k, int n) {
        backtracking(k,n,1,0);
        return result;
    }
    public void backtracking(int k,int targetSum,int startIndex,int sum){
        //剪枝操作
        if(sum>targetSum){
            return;
        }
        //确定终止条件
        //目标数组长度达到k,且之和为n
        if(path.size() == k && sum == targetSum){
            result.add(new ArrayList<>(path));
            return;
        }
        //确定单层循环逻辑
        for (int i = startIndex; i <= 9-(k-path.size())+1 ; i++) {
            //处理节点
            path.add(i);
            sum+=i;
            //递归函数
            backtracking(k,targetSum,i+1,sum);
            //回溯操作
            sum-=i;
            path.removeLast();
        }
    }
}