力扣刷题笔记-旋转图像

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

分析：

解决这个问题最主要是要找到旋转前后的元素和旋转之前的元素有什么对应关系。

设某个元素在原矩阵中位于：第 i 行，第 j 列，考虑顺时针旋转90度之后的坐标会变成什么样。

先看最容易想象的四个角。

左上角 (0, 0)，顺时针旋转之后位置变成了右上角(0, n-1)。

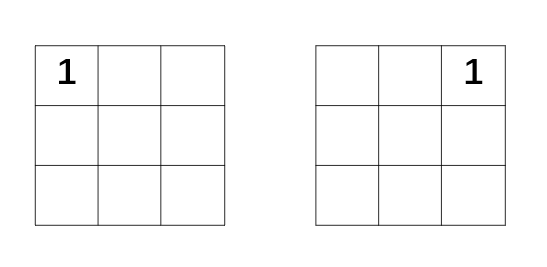
从这个变化可以得到最后行号没有变（仍然是 0），列号从 0 变成了 n − 1（方向发生反转）

再观察"整条边"的变化，先看原矩阵中最上面的一整行(0,0) (0,1) (0,2) ...顺时针旋转 90° 后，它会变成最右边的一整列

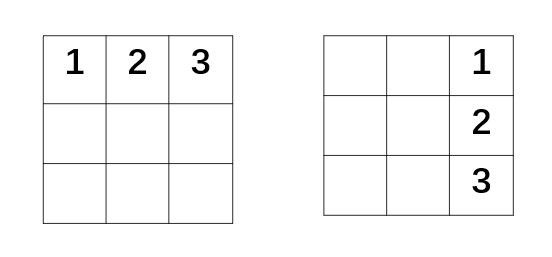
可以得到一个思路，原来横着数的关系，变成了竖着数的关系。从而可以联想到也许可以考虑先把行和列互换，而矩阵中行和列互换的操作就是转置。转置后先看一下：

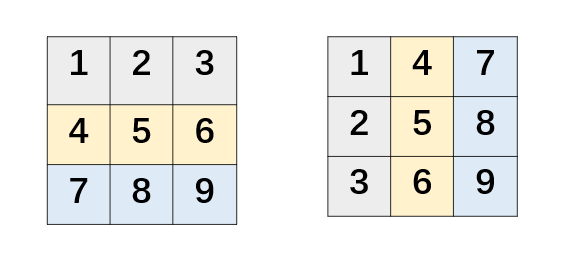
转置之后左边变成了右边，转置后再对比下这个矩阵和我们最终要生成的矩阵。转置能做到的是：(i, j) → (j, i)，也就是说：最上面一行 → 最左边一列，但我们要做的是最上面一行 → 最右边一列。直观对比两个矩阵就能发现，每一行的元素的方向不对，反了。

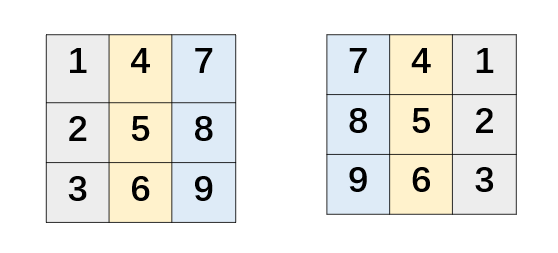
可以看到，只需要再把每一行的元素反转一下，就是最后的矩阵了

所以最终我们只需要进行两步操作就可以实现顺时针旋转90度：

矩阵转置
每一行元素左右翻转
C++代码实现：

cpp 复制代码

#include<iostream>
#include<vector>
using namespace std;
class Solution {
public:
	void rotate(vector<vector<int>>& matrix) {
		//沿主对角线转置,把 matrix[i][j] 和 matrix[j][i] 交换
		int n = matrix.size();
		for (int i = 0; i < n; i++) {
			for (int j = i + 1; j <n; j++) {
				swap(matrix[i][j], matrix[j][i]);
			}
		}
		// 对每一行进行左右翻转
		for (int i = 0; i < n; i++) {
			reverse(matrix[i].begin(), matrix[i].end());
		}
	}
};

关于矩阵转置，矩阵可以分成三部分：

css 复制代码

×  ○  ○
○  ×  ○
○  ○  ×

×代表主对角线，在转置的过程中是不用动的。为了完成转置，可以只用走一半，专注于处理对角线以上的部分，处理的时候把每个数和对角线以下的部分进行交换就可以了，每次处理的时候都会去处理一对 (i,j) 和 (j,i) ，让这两个数都完成交换，到自己最终的位置去。