算法（十三）回溯算法---N皇后问题

文章目录

算法概念
[经典例子 - N皇后问题](#经典例子 - N皇后问题)
- 什么是N皇后问题？
- 实现思路

算法概念

回溯算法是 类似枚举的深度优先搜索尝试过程，主要是再搜索尝试中寻找问题的解 ，当发生不满足求解条件时 ，就会"回溯"返回 （也就是递归返回），尝试别的路径求解。

经典例子 - N皇后问题

什么是N皇后问题？

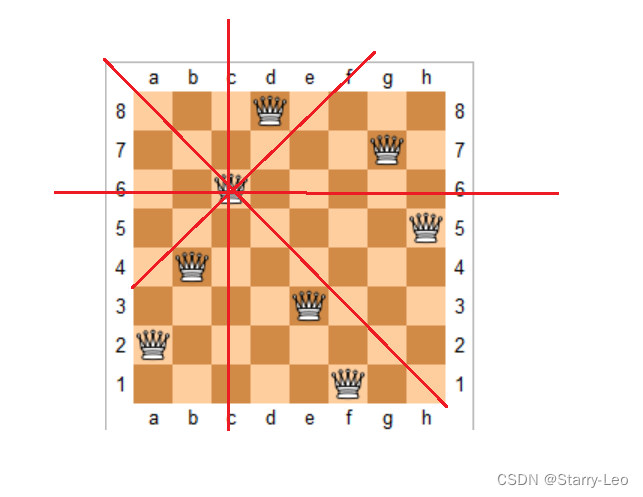
N皇后问题研究的是：如何将ｎ个皇后放在n * n的棋盘上，并且使皇后彼此之间不能相遇，也就是一个皇后的上下左右、以及斜着对角线上都不能有另外一个皇后，也就是一个皇后在 "米" 的视线中不能遇到另外一个皇后。

实现思路

如上图，我们可以把这个问题划分成8个阶段，依次将8个棋子放到第一行、第二行...第八行。在放置的过程中，我们不停的检查当前的方法是否满足要求。如果满足，继续下一行放置，如果不满足，就再换一种方法，继续尝试。

实现代码：

bash 复制代码

package com.xxliao.algorithms.backtrack;

/**
 * @author xxliao
 * @description: N皇后问题 求解
 * @date 2024/6/1 0:14
 */
public class NQueens {

    public static void main(String[] args) {
        NQueens queens=new NQueens();
        queens.setQueens(0);
        queens.printQueens();
    }

    // 皇后数量
    static int queens_count = 8;
    // 定义数组来存在皇后，索引表示行，值表示皇后存在改行的那一列中
    int[] array = new int[queens_count];

    /**
     * @description  根据行号，设置该行的皇后位置
     * @author  xxliao
     * @date  2024/6/1 0:17
     */
    public void setQueens(int row) {
        if(row == queens_count) {
            // 递归结束条件
            return;
        }
        // 尝试每一列放置，如果没有合适的，就返回上一层
        for(int column = 0; column <queens_count; column++) {
            if(isOk(row,column)) {
                // 符合条件，放置
                array[row] = column;
                // 然后设置下一行
                setQueens(++row);
            }
        }
    }

    /**
     * @description  判断改行该列是否 符合条件
     * @author  xxliao
     * @date  2024/6/1 0:23
     */
    private boolean isOk(int row, int column) {
        // 定义左上角、右上角 列索引标记
        int leftup = column - 1;
        int rightup = column + 1;
        // 然后从当前行逐行向上遍历，看当前row、column是否满足条件
        for(int i = row-1; i >= 0; i--) {
            if(array[i] == column){
                // 如果该位置已经有了皇后了，不满足
                return false;
            }
            if(leftup >=0 && array[i] == leftup) {
                //左上对角线存在queen,第一次执行是当前行，肯定不满足条件，i--，leftup--之后就是当前点的左上角位置
                return false;
            }
            if(rightup < queens_count && array[i] == rightup) {
                //右下对角线存在queen，同上理由
                return false;
            }
            leftup--;
            rightup++;
        }
        return true;
    }

    /**
     * @description  打印N皇后棋盘
     * @author  xxliao
     * @date  2024/6/1 0:34
     */
    private void printQueens() {
        for (int i = 0; i < queens_count; i++) {
            for (int j = 0; j < queens_count; j++) {
                if (array[i] == j) {
                    System.out.print("Q| ");
                }
                else {
                    System.out.print("*| ");
                }
            }
            System.out.println();
        }
        System.out.println("-----------------------");
    }
}

演示结果：