UVa11604 General Sultan

题目链接
题意
分析
[AC 代码](#AC 代码)

题目链接

UVA - 11604 General Sultan

题意

给出一些0和1组成的模式串，问是否存在一个串使得有多种方案将这个串分解成模式串。

给一个包含n（n≤100）个符号的二进制编码方式，是否存在一个二进制序列，存在至少两种解码方法。比如{a=01, b=001, c=01001}是有歧义的，因为01001可以解码为a+b或者c。每个编码由不超过20个0或1组成。

分析

很好的一道图论建模题目！思路来自于HouseFangFZC的博文。

先看一个两种方案去拼接形成同一个串的图：

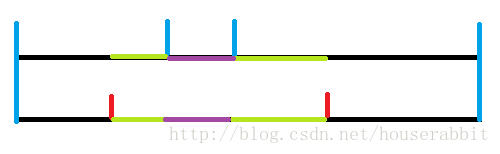
可以发现总是一个方案新追加的串和另一个方案当前未匹配部分做匹配，并且其中一者完全匹配掉，另一者有剩余部分（或者另一者也匹配完，即找到了两种不同拼接方案）。

将每个模式串的每一个字符看成一个结点，并额外增加起点s、终点t两个虚拟结点。首先起点与每个模式串的首字母连一条有向边。对于第i个模式串，考虑其第 h i h_i hi个字符开始的子串（对应节点u），若其与第j个模式串做匹配（注意 h i = 0 h_i=0 hi=0时， j ≠ i j\ne i j=i）满足至少一者匹配到结尾，则连有向边，分三种情况：若两者都匹配完，则 u → t u\rightarrow t u→t；若模式串j的首个未匹配字符是 h j h_j hj（对应节点v），则 u → v u\rightarrow v u→v；若子串 h i h_i hi的首个未匹配字符是 h x h_x hx（对应节点w），则 u → w u\rightarrow w u→w。

有向图建完后，跑一遍dfs，看起点s能否到达终点t就能解决问题。

AC 代码

cpp 复制代码

#include <iostream>
#include <cstring>
using namespace std;

#define L 22
#define N 101
int g[N*L][N*L], c[N*L], e[N], t[N], m, n, kase = 0; char s[N][L], tmp[L]; bool vis[N*L];

int common(int i, int h, int j) {
    int k = 0;
    while (h < e[i]) {
        if (s[i][h] != s[j][k]) return k;
        ++h; ++k;
    }
    return k;
}

bool dfs(int u = 0) {
    if (u == m) return true;
    vis[u] = true;
    for (int i=0, v; i<c[u]; ++i) if (!vis[v = g[u][i]] && dfs(v)) return true;
    return false;
}

void solve() {
    memset(c, 0, sizeof(c)); memset(vis, 0, sizeof(vis));
    for (int i=0; i<n; ++i) cin >> tmp >> s[i], e[i] = strlen(s[i]), g[0][c[0]++] = t[i] = i<1 ? 1 : t[i-1] + e[i-1];
    m = t[n-1] + e[n-1];
    for (int i=0; i<n; ++i) for (int j=0; j<e[i]; ++j) for (int k=0; k<n; ++k) {
        if (i==k && j==0) continue;
        int cc = common(i, j, k), u = t[i]+j;
        if (cc == e[k] && cc+j == e[i]) g[u][c[u]++] = m;
        else if (cc < e[k] && cc+j == e[i]) g[u][c[u]++] = t[k] + cc;
        else if (cc == e[k] && cc+j < e[i]) g[u][c[u]++] = u + cc;
    }
    cout << "Case #" << ++kase << (dfs() ? ": Ambiguous." : ": Not ambiguous.") << endl;
}

int main() {
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    while (cin >> n && n) solve();
    return 0;
}