2025牛客多校第九场 G.排列 A.AVL树 F.军训 个人题解

F.军训

数学 #曼哈顿距离

题目

思路

首先很容易想到的是，一定可以通过旋转到达目标状态，不会有-1的情况

接下来是一个关键的观察：关注双脚所在中点的移动

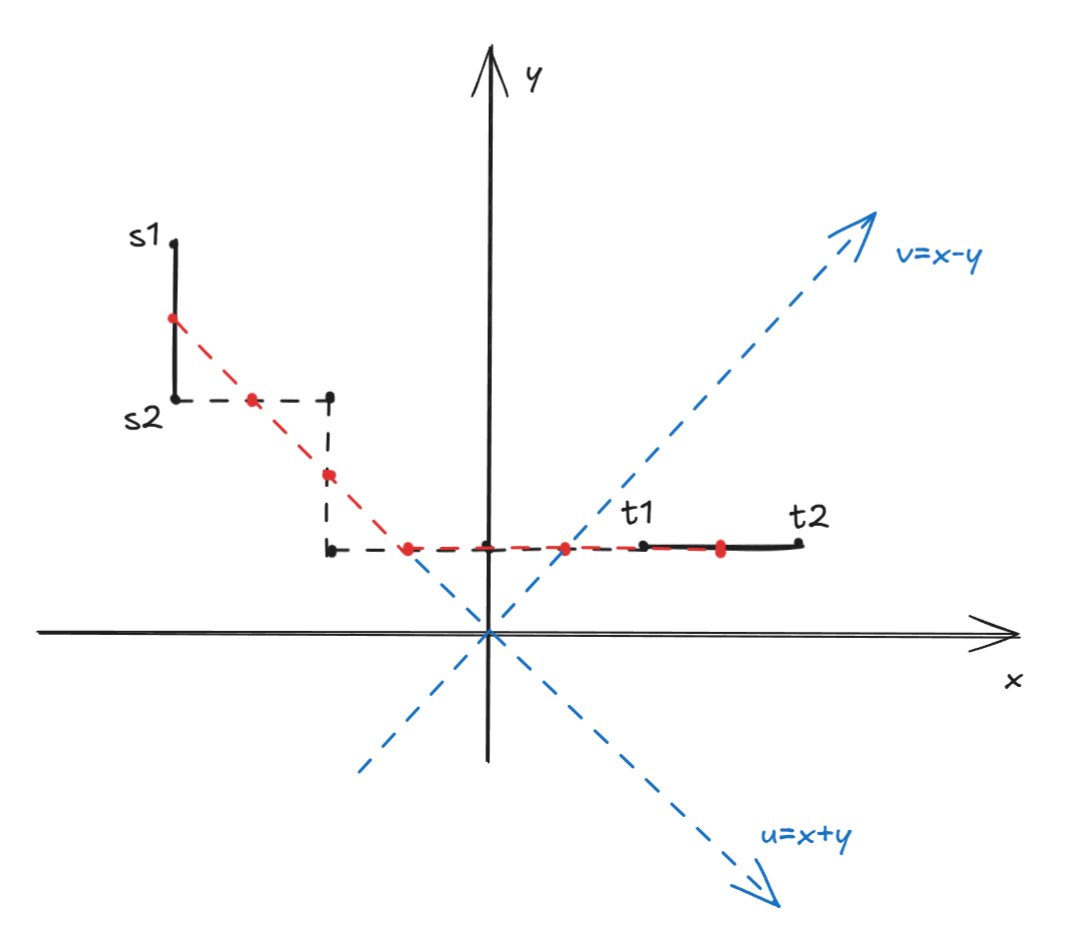
发现实际上中点移动一个单位曼哈顿距离就代表一次旋转

因此进行坐标变换即可

代码实现

#include<iostream>
#include<vector>
#include<map>
#include<cmath>
#include<set>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(int i = (a); i <= (b); i ++)
#define per(i, a, b) for(int i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
constexpr ll inf = 1e9 + 5;
#define int ll 
#define double long double
void trans(double&x,double&y){
    double u=x+y,v=x-y;
    x=u,y=v;
}

void eachT() {   
    int sx1,sy1,sx2,sy2,tx1,ty1,tx2,ty2;
    cin>>sx1>>sy1>>sx2>>sy2>>tx1>>ty1>>tx2>>ty2;
    double sx=1.0*(sx1+sx2)/2,sy=1.0*(sy1+sy2)/2;
    double tx=1.0*(tx1+tx2)/2,ty=1.0*(ty1+ty2)/2;
    trans(sx,sy),trans(tx,ty);
    double dis=abs(sx-tx)+abs(sy-ty);
    cout<<(int)dis<<'\n';
}

signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    ll t = 1;
    cin >> t;
    while (t--) {
        eachT();
    }
}

---

A.AVL树

树上dp #dp #dfs

题目

思路

本题是一个比较巧妙的树上dp，状态设置较为特殊

状态含义：
\(dp[u][h]\)表示将节点\(u\)及其子树修改为高度为\(h\)的\(AVL\)树所需要的最少操作次数

状态转移：

\[\begin{align} &dp[u][h]=min\{ dp[u][h],dp[lson][h-1]+dp[rson][h-1] \}\\ \\ &dp[u][h]=min\{ dp[u][h],dp[lson][h-2]+dp[rson][h-1] \}\\ \\ &dp[u][h]=min\{ dp[u][h],dp[lson][h-1]+dp[rson][h-2] \} \end{align} \]

由于两棵子树的高度差不能超过1，所以枚举左右子树的三种情况进行状态转移

注意到转移最开始的时候需要调用\(dp[u][0]\)的值，其含义为：将\(u\)及其子树完全删除所需要的最少操作次数，因此该值即为\(u\)的子树大小\(size\)，跑一遍\(dfs\)预处理即可

最麻烦的事情是\(dp[0][h]\)，若\(u\)没有左儿子，那么其\(lson\)的值即为\(0\)，此时dp需要访问\(dp[0][h]\)的值，代表构建一棵高度为\(h\)的\(AVL\)树所需要的最小操作次数

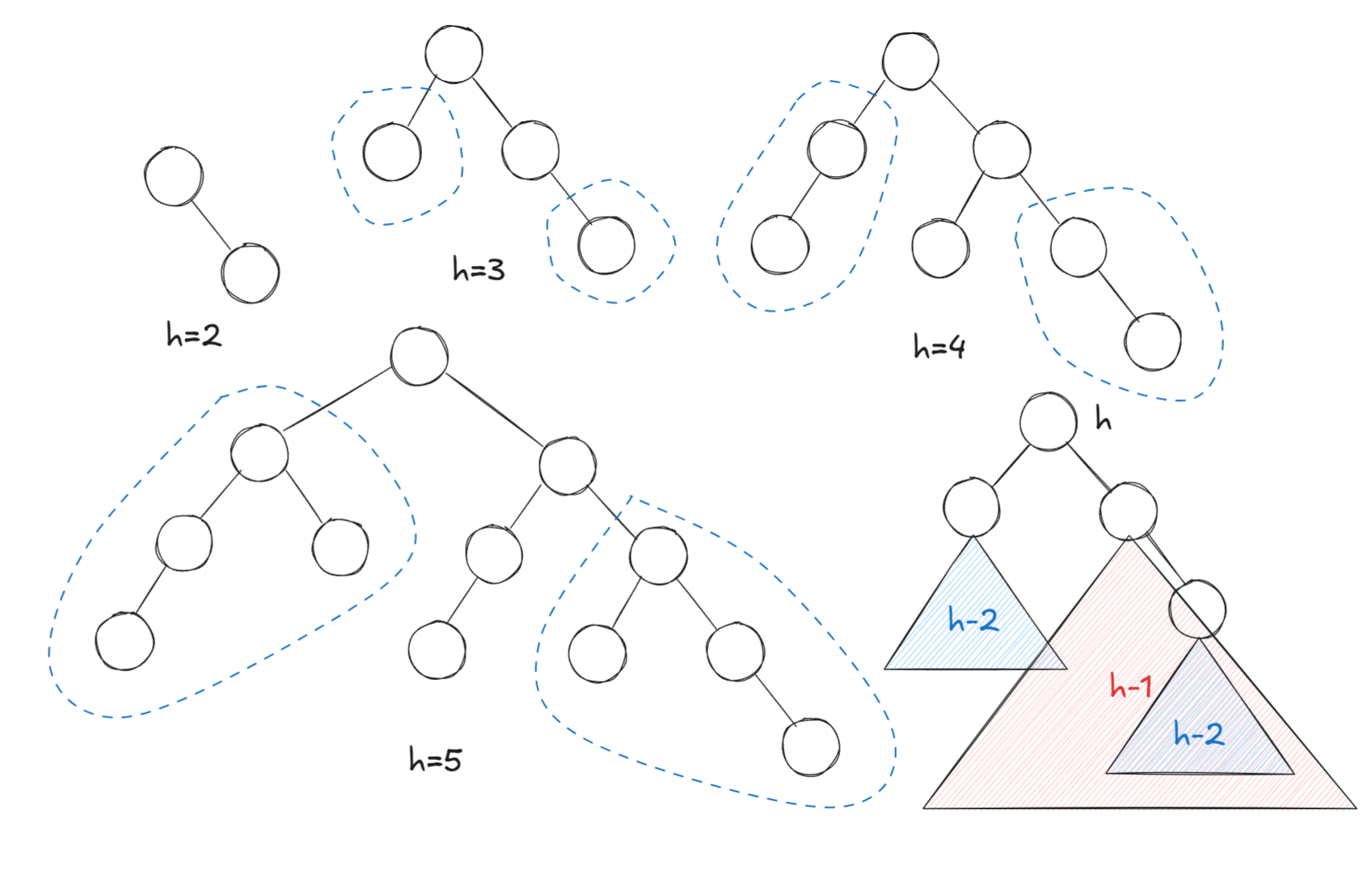
画出高度为\(2,3,4,5\)的最简\(AVL\)树，会发现子树之间存在特别的递推关系：

当前子树必定等于其爷爷节点的另一个子树，

当前子树大小等于孙子子树大小加上另一个儿子子树大小再加上自己本身

即：

\[dp[0][h]=dp[0][h-1]+dp[0][h-2]+1 \]

至此可以完成树上dp的全过程

代码实现

#include<iostream>
#include<vector>
#include<unordered_map>
#include<cmath>
#include<string>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(ll i = (a); i <= (b); i ++)
#define per(i, a, b) for(ll i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
constexpr ll inf = 1e9 + 5;

const int N=2e5+5,H=40;
int dp[N][H],n;

void init(){
    dp[0][1]=1,dp[0][2]=2;
    rep(i,3,H-1){
        dp[0][i]=dp[0][i-1]+dp[0][i-2]+1;
    }
}

struct node{
    int ls,rs,siz;
}a[N];

int dfs(int u){
    if(u==0)return 0;
    a[u].siz=1;
    a[u].siz+=dfs(a[u].ls);
    a[u].siz+=dfs(a[u].rs);
    dp[u][0]=a[u].siz;
    rep(i,1,H-1)dp[u][i]=inf;
    return a[u].siz;
}

void dfs2(int u){
    if(u==0)return;
    dfs2(a[u].ls);
    dfs2(a[u].rs);
    int ls=a[u].ls,rs=a[u].rs;
    rep(j,1,H-1){
        dp[u][j]=min(dp[u][j],dp[ls][j-1]+dp[rs][j-1]);
        if(j-2>=0)dp[u][j]=min(dp[u][j],dp[ls][j-2]+dp[rs][j-1]);
        if(j-2>=0)dp[u][j]=min(dp[u][j],dp[ls][j-1]+dp[rs][j-2]);
    }
}

void eachT() {
    cin>>n;
    rep(i,1,n){
        cin>>a[i].ls>>a[i].rs;
    }
    dfs(1);
    dfs2(1);
    int ans=inf;
    rep(j,0,H-1){
        ans=min(ans,dp[1][j]);
    }
    cout<<ans<<'\n';
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    ll t = 1;
    init();
    cin >> t;
    while (t--) {
        eachT();
    }
}

---

G.排列

组合数 #笛卡尔树 #dfs

题目

思路

考虑一组样例：

\[5,3,6,4,1,7,2 \]

操作分为删去与打印两种，若想要打印数字\(i\)，则\(i\)必须为当前序列的最小值

因此发现打印的可行性具有一定的顺序，比如我想打印\(4\)，那么必然要先将\(1,2,3\)删去

而删去的过程中又必然会将某些经过的点提前删去，因此尝试画出路径图：

发现这实际上就是一棵笛卡尔树！

• 树中节点的左右关系与原序列中的一致
• 树中的父亲节点必定比左右儿子要小，对应着必须先走过小的节点才能走到大的节点

接下来就是如何"数数"了：

我们可以通过打印序列的最后一个元素是谁，来进行分类

这样分类的依据就在于，每次打印的元素必然是序列中的最小元素，因此枚举每个数作为最后一个打印的数，不会出现情况间的重复与遗漏

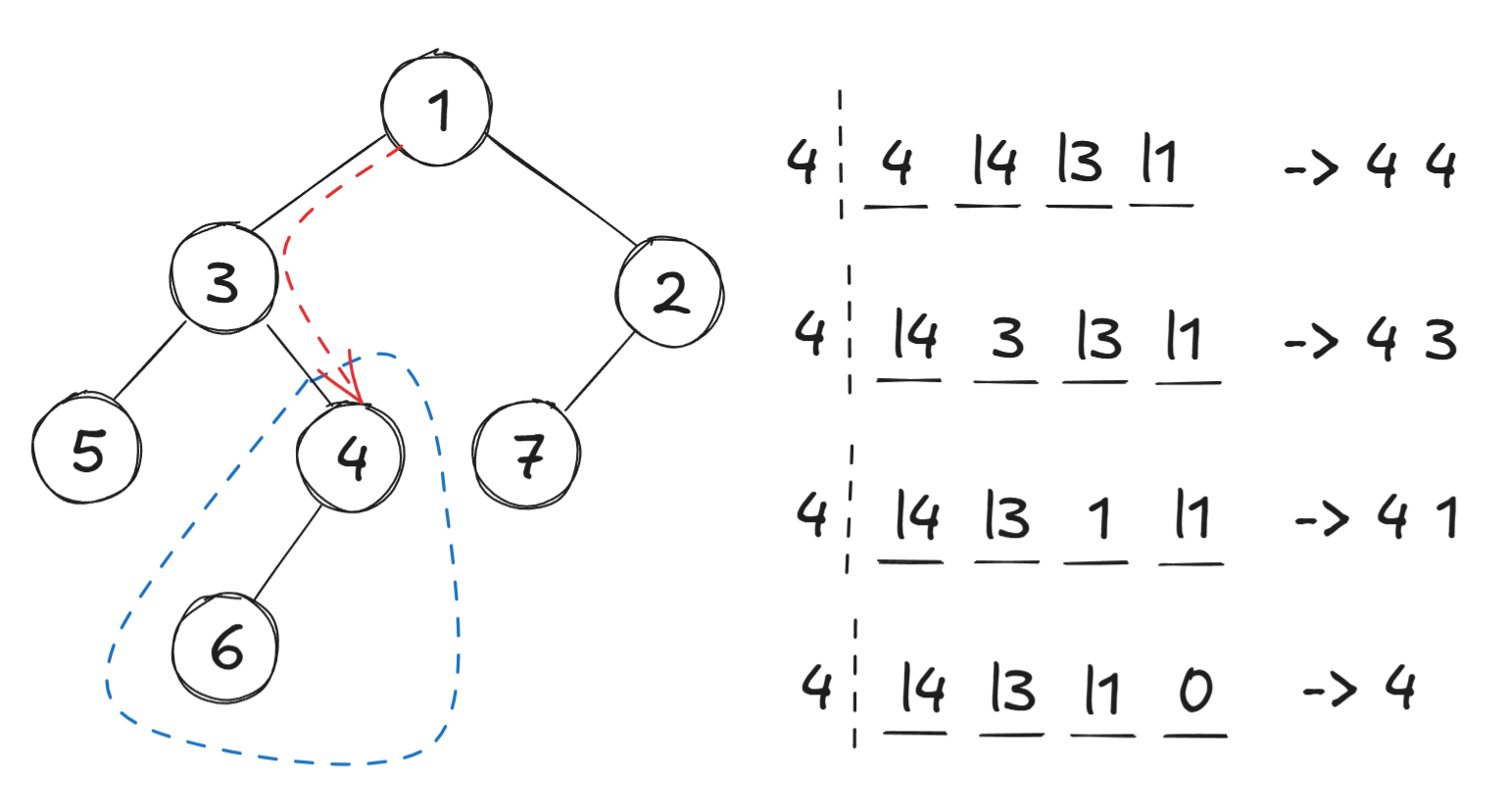
以数字\(4\)为例，想要走到四号节点，必然需要先删去某些节点

• 比4大的1、3必然要删除
• 原序列中，在3左边、1右边的所有数都要删除，这样才能删掉1、3
  综上 ，发现保留下来的数正好就是4所在的子树（蓝色区域）

由于删除操作已经占了\(n-size[u]\)次，那么能够打印序列的最大长度正是\(size[u]\)

若把左边看作最后一次打印的元素，右边看作第一次打印的元素，那么会发现打印序列是一个单调不增序列，并且开头元素固定为4

开头固定的单调不减序列有多少种方案数？

自然是使用占位置的隔板法进行统计：

• 能够出现在打印序列中的数字必然是比4小且靠中间的位置，即沿着4往根部走，途中遇到的所有数字
• 能够打印的数字的数量即为4的深度-1，\(dep-1\)，即1、3两个数字
• 因此有\(l_{4},l_{3},l_{1}\)三块隔板，\(l_{i}\sim l_{i-1}\)间填数字\(i-1\)即可构造单调不增序列
• \(l_{1}\)的右边没有东西，填0代表空着，这也对应了长度小于\(size[u]\)的情况
  因此方案数计算公式为：

\[C_{size[u]+dep[u]-1}^{dep[u]} \]

在dfs回溯过程中，\(size[u],dep[u]\)均已知，可以直接算答案

因此一遍dfs即可算出答案

代码实现

#include<iostream>
#include<vector>
#include<unordered_map>
#include<cmath>
#include<stack>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(ll i = (a); i <= (b); i ++)
#define per(i, a, b) for(ll i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
constexpr ll inf = 1e9 + 5;
#define int ll 
const int N=1e6+5,mod=998244353;
int n;

int qpow(int a,int b){
    a%=mod;int res=1;
    while(b){
        if(b%2){res*=a;res%=mod;}
        a*=a;a%=mod;b>>=1;
    }
    return res%mod;
}
vector<int>A,inv;
void inv0(int len){
    A.resize(len+1),inv.resize(len+1);
    A[0]=1;inv[0]=1;
    rep(i,1,len){
        A[i]=(A[i-1]*i)%mod;
        inv[i]=qpow(A[i],mod-2);
    }
}
int C(int n,int m){
    if(m>n)return 0;
    return A[n]*inv[m]%mod*inv[n-m]%mod;
}

struct node{
    int ls,rs;
}a[N];

int ans;

int dfs(int u,int dep){
    if(u==0)return 0;
    int siz=1;
    int ls=a[u].ls,rs=a[u].rs;
    siz+=dfs(ls,dep+1)+dfs(rs,dep+1);
    ans+=C(siz+dep-1,dep);
    ans%=mod;
    return siz;
}

void eachT() {   
    rep(i,1,n){
        a[i].ls=a[i].rs=0;
    }
    cin>>n;
    stack<int>st;
    rep(i,1,n){
        int x;cin>>x;
        if(st.empty())st.push(x);
        else{
            if(x<st.top()){
                int son=0;
                while(!st.empty()&&x<st.top()){
                    son=st.top();st.pop();
                }
                a[x].ls=son;
                if(!st.empty())a[st.top()].rs=x;
                st.push(x);
            }else{
                a[st.top()].rs=x;
                st.push(x);
            }
        }
    }
    ans=0;
    dfs(1,1);
    cout<<(ans+1)%mod<<'\n';
}

signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    inv0(5e6+5);
    ll t = 1;
    cin >> t;
    while (t--) {
        eachT();
    }
}