文章目录
int底层源码
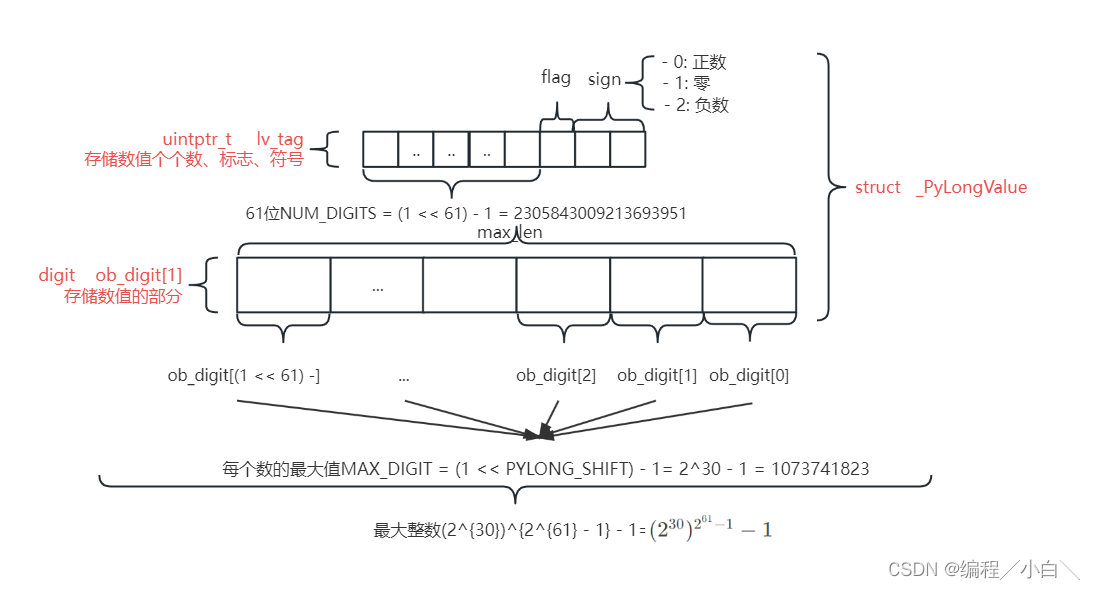
python 的int类型貌似并没有一个位数上线,然而我们知道其他语言的整数都是有位数,一般为32位或者64位等,那么python是怎么实现int类型没有位数限制的呢,下面这段代码是cpython仓库中实现python int的代码,int被定义为_longobject 的结构体,它的数字部分是一个_PyLongValue 的结构体,_PyLongValue 结构体有两个属性:
ob_digit是一个无符号整型的数组初始化长度为1,后续长度会动态改变,用于存储数字ob_digit中的每一个长整数由多个 30 位或 15 位的digit组成,具体取决于平台。- 一个是
lv_tag被用于存储int数据的数字个数、符号和标志 lv_tag的位分配 :- 高位(
ndigits = lv_tag >> _PyLong_NON_SIZE_BITS)存储的是长整数中的"数字"个数(ndigits)。 - 低
2位存储符号信息:- 0: 正数
- 1: 零
- 2: 负数
- 第三低位(当前未使用)保留用于"immortality flag"(不死标志)。
- 高位(
- 数字的个数(
ndigits)存储在lv_tag的高位部分。
因此python中的int的长度是根据其lv_tag所能表示Number of digits(数字的个数)来决定的,由于uintptr_t在32位与64位操作系统所表示的整数是不同的因此,python的位数也是不同的
c
#if PYLONG_BITS_IN_DIGIT == 30
typedef uint32_t digit; // 指定了每个数字的类型
typedef int32_t sdigit;
typedef uint64_t twodigits;
typedef int64_t stwodigits;
#define PyLong_SHIFT 30
#define _PyLong_DECIMAL_SHIFT 9
#define _PyLong_DECIMAL_BASE ((digit)1000000000)
#elif PYLONG_BITS_IN_DIGIT == 15
typedef unsigned short digit; // 指定了每个数字的类型
typedef short sdigit;
typedef unsigned long twodigits;
typedef long stwodigits;
#define PyLong_SHIFT 15
#define _PyLong_DECIMAL_SHIFT 4
#define _PyLong_DECIMAL_BASE ((digit)10000)
#else
#error "PYLONG_BITS_IN_DIGIT should be 15 or 30"
#endif
/******************上面的代码主要是根据不同的平台定义整数中每个元素的位数*************************/
#define PyLong_BASE ((digit)1 << PyLong_SHIFT)
#define PyLong_MASK ((digit)(PyLong_BASE - 1))
#define PyObject_HEAD PyObject ob_base;
#define _PyLong_SIGN_MASK 3 // 用于获得符号位
#define _PyLong_NON_SIZE_BITS 3 // 用于获得ob_digit元素的个数
typedef struct _PyLongValue {
uintptr_t lv_tag; /* Number of digits, sign and flags */
digit ob_digit[1];
} _PyLongValue;
struct _longobject {
PyObject_HEAD
_PyLongValue long_value;
};- 这段代码根据
PYLONG_BITS_IN_DIGIT的值定义了不同大小的digit和twodigits类型,并定义了一些与长整数表示相关的常量。 PyLong_SHIFT定义了每个digit的位数。_PyLong_DECIMAL_SHIFT和_PyLong_DECIMAL_BASE定义了十进制表示中的一些常量。
最大整数推断
假设 lv_tag 为一个 64 位的 uintptr_t,并且 PYLONG_BITS_IN_DIGIT 为 30:
c
uintptr_t lv_tag = ...; // 假设这个值已经被设置
int num_digits = lv_tag >> _PyLong_NON_SIZE_BITS; // 提取数字的个数
int sign = lv_tag & _PyLong_SIGN_MASK; // 提取符号- 通过
lv_tag >> _PyLong_NON_SIZE_BITS提取lv_tag的高位部分,可以得到长整数中的数字个数(ndigits)。 - 通过
lv_tag & _PyLong_SIGN_MASK提取lv_tag的低 2 位,可以得到长整数的符号。 - 数值的绝对值计算公式:
absolute value = ∑ i = 0 ndigits − 1 ob_digit [ i ] × 2 PyLong_SHIFT × i \text{absolute value} = \sum_{i=0}^{\text{ndigits}-1} \text{ob\_digit}[i] \times 2^{\text{PyLong\_SHIFT} \times i} absolute value=i=0∑ndigits−1ob_digit[i]×2PyLong_SHIFT×i
那我们可以从中推断python所能表示的最大整数, - 首先我们假设
PyLong_SHIFT和PYLONG_BITS_IN_DIGIT是30, - 因此我们可以计算出
ob_digit中每个元素的最大值为MAX_DIGIT = (1 << PYLONG_SHIFT) - 1= 2^30 - 1 = 1073741823 - 接着我们可以根据
lv_tag是一个64位的无符号整数,其最低3为符号标志,那么前61位是所能表示的整数的个数num_digits最大值NUM_DIGITS = (1 << 61) - 1 = 2305843009213693951 - 那么
python所能表示的最大整数是 ∑ i = 0 num_digits − 1 ( 2 30 − 1 ) × 2 30 i = ( 2 30 ) 2 61 − 1 − 1 \sum_{i=0}^{\text{num\_digits}-1} (2^{30} - 1) \times 2^{30i} = (2^{30})^{2^{61} - 1} - 1 ∑i=0num_digits−1(230−1)×230i=(230)261−1−1,这个数字大到已经远超内存限制
对于一个由
num_digits个 30 位digit组成的最大整数,其值表示为:max_int = ∑ i = 0 num_digits − 1 ( 2 30 − 1 ) × 2 30 i \text{max\int} = \sum{i=0}^{\text{num\_digits}-1} (2^{30} - 1) \times 2^{30i} max_int=∑i=0num_digits−1(230−1)×230i
我们可以将这个求和公式拆开来看: max_int = ( 2 30 − 1 ) × ( 1 + 2 30 + 2 60 + ... + 2 30 ( num_digits − 1 ) ) \text{max\_int} = (2^{30} - 1) \times (1 + 2^{30} + 2^{60} + \ldots + 2^{30(\text{num\_digits} - 1)}) max_int=(230−1)×(1+230+260+...+230(num_digits−1))
注意到括号内的部分是一个几何级数,其公比为 2 30 2^{30} 230,项数为
num_digits。对于一个等比数列 1 + r + r 2 + ... + r n − 1 1 + r + r^2 + \ldots + r^{n-1} 1+r+r2+...+rn−1,它的和为: S = r n − 1 r − 1 S = \frac{r^n - 1}{r- 1} S=r−1rn−1
在这里, r = 2 30 r = 2^{30} r=230,而项数 n = num_digits n = \text{num\_digits} n=num_digits。
所以: 1 + 2 30 + 2 60 + ... + 2 30 ( num_digits − 1 ) = ( 2 30 ) num_digits − 1 2 30 − 1 1 + 2^{30} + 2^{60} + \ldots + 2^{30(\text{num\_digits} - 1)} = \frac{(2^{30})^{\text{num\_digits}} - 1}{2^{30} - 1} 1+230+260+...+230(num_digits−1)=230−1(230)num_digits−1
将这个结果代入最大整数公式中,我们得到: max_int = ( 2 30 − 1 ) × ( 2 30 ) num_digits − 1 2 30 − 1 \text{max\_int} = (2^{30} - 1) \times \frac{(2^{30})^{\text{num\_digits}} - 1}{2^{30} - 1} max_int=(230−1)×230−1(230)num_digits−1
可以简化为: max_int = ( 2 30 ) num_digits − 1 \text{max\_int} = (2^{30})^{\text{num\_digits}} - 1 max_int=(230)num_digits−1
num_digits的最大值为: num_digits = 2 61 − 1 \text{num\_digits} = 2^{61} - 1 num_digits=261−1将这个值代入最大整数公式中,我们得到: max_int = ( 2 30 ) 2 61 − 1 − 1 \text{max\_int} = (2^{30})^{2^{61} - 1} - 1 max_int=(230)261−1−1
因为python的符号位并不影响存储数字的大小以及个数,所以其最小整数的绝对值与最大正数的绝对值相同