文章目录
前言
本篇博客讲解《算法设计与分析》(耿国华版)第四章:贪心算法的内容,更多贪心相关内容可以查看本人其他博客:
贪心相关概念
贪心算法通过做一系列的贪心选择,给出某一问题的最优解。
对算法中的每一个决策点做出当时看起来最佳的选择。
贪心算法的基本步骤:
(1)选择合适的贪心策略;
(2)根据贪心策略,写出贪心选择的算法,求得最优解;
(3)证明在此策略下,该问题具有贪心选择性质和最优子结构性质,
贪心算法经常需要排序。
贪心法不能保证问题总能得到最优解。
算法积累
1.部分背包问题
有 N 件物品和一个容量为 V 的背包。放入第 i 件物品耗费的空间是 Ci,得到的价值是 Wi,物品可以分割。求解将哪些物品装入背包可使价值总和最大。
- 每次选择密度最高的物品
C++
#include<bits/stdc++.h>
using namespace std;
struct albb
{
int m;
int v;
double avg;
}al[101];
bool cmp(albb a,albb b)
{
return a.avg>b.avg;
}
int main()
{
int n,t;
cin>>n>>t;
for(int i=0;i<n;i++)
{
cin>>al[i].m>>al[i].v;
al[i].avg = 1.0 * al[i].v/al[i].m;
}
sort(al,al+n,cmp);
double ans,weight=0;
for(int i=0;i<n;i++)
{
if(weight + al[i].m <= t)
{
weight += al[i].m;
ans += al[i].v;
}
else
{
ans += al[i].avg * (t-weight);
break;
}
}
printf("%.2lf\n",ans);
return 0;
}- 大小比较也可以用重载小于号的方法
C++
#include<bits/stdc++.h>
using namespace std;
struct albb
{
int m;
int v;
double avg;
bool operator < (const albb &a) const
{
return a.avg < avg;
}
}al[101];
int main()
{
int n,t;
cin>>n>>t;
for(int i=0;i<n;i++)
{
cin>>al[i].m>>al[i].v;
al[i].avg = 1.0 * al[i].v/al[i].m;
}
sort(al,al+n);
double ans,weight=0;
for(int i=0;i<n;i++)
{
if(weight + al[i].m <= t)
{
weight += al[i].m;
ans += al[i].v;
}
else
{
ans += al[i].avg * (t-weight);
break;
}
}
printf("%.2lf\n",ans);
return 0;
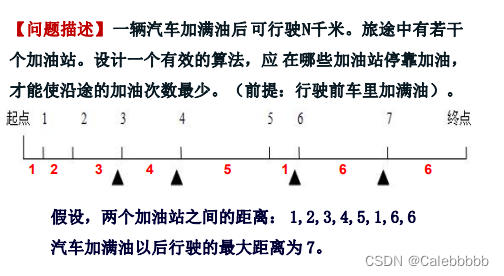
}2.汽车加油
- 唯一的度量标准就是我们加满油后已经走过的路程与即将所走的一段路程之和是否超过汽车的最大行驶路程,如果超过,则在该加油站加油,反之则出发
C++
#include <bits/stdc++.h>
using namespace std;
const int maxn = 100;
int a[maxn];//加油站之间的距离
int n, k;
int found(int a[])
{
int count = 0;
int road = 0;
for (int i = 0; i <= k; i++)
{
if (a[i] > n)
{
cout << "地点不可及" << endl;
return -1;
}
}
cout << "需要加油的的加油站为:" ;
for (int i = 0; i <= k; i++)
{
road += a[i];//已经走的路程与即将要走的路程相加
if (road > n)
{//若结果超过汽车的最大限度
count++;//需要加油
road = a[i];//油箱加满油
cout << i << " ";//输出加油的加油站
}
}
cout << endl;
return count;
}
int main()
{
cout << "请输入汽车满油可行驶的距离和旅途中加油站的个数:" << endl;
cin >> n >> k;
cout << "请依次输入各个加油站之间的距离:" << endl;
for (int i = 0; i <= k; i++)
cin >> a[i];
int count = found(a);
if (count >= 0)
cout << "最少加油次数为:" << count << endl;
return 0;
}3.活动安排(区间选点/最大不相交区间问题)
假设n个活动都需要使用某一场地,但场地在任何时刻只能被一个活动所占用, 且一旦开始不能被中断。 活动i有一个开始时间si和结束时间ei(si<ei),对于活动i和活动j,如果si≥ej或sj≥ei,则称这两个活动兼容。设计算法求一种最优活动安排方案,使得在某时间段内安排的活动个数最多。
- 将每个区间按照右端点从小到大排序
- 从前往后枚举每个区间:(1)如果当前区间已经包含点,则pass(2)否则,选择当前区间右端点
- 选择右端点是为了覆盖尽可能多的区间
- 每次都是一个局部最优解
C++
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
struct Range
{
int l, r;
bool operator< (const Range &W)const //重载小于号
{
return r < W.r;
}
}range[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d%d", &range[i].l, &range[i].r);
sort(range, range + n);
int res = 0, ed = -2e9;
for (int i = 0; i < n; i ++ )
if (range[i].l > ed)
{
res ++ ;
ed = range[i].r;
}
printf("%d\n", res);
return 0;
}4.农场畜栏(区间分组问题)
农场有n头牛,每头牛会有一个特定的时间区间[s,e]在蓄栏里挤牛奶,并且一个蓄栏里任何时刻只能有一头牛挤奶。现在农场主希望知道最少需要多少蓄栏能够满足上述要求,并给出每头牛被安排的方案。对于多种可行方案,输出一种即可。
- 将所有区间按照左端点从小到大排序
- 从前往后处理每个区间,判断能否将其放到某个现有的组中去(1)如果不存在这样的组,则开一个新组,将其放进去(2)如果存在这样的组,则将其放进去,并更新右端点的最大值
C++
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int n;
struct Range
{
int l, r;
bool operator< (const Range &W)const //重载小于号
{
return l < W.l;
}
}range[N];
int main()
{
cin >> n;
for (int i = 0; i < n; i ++ )
{
int l, r;
cin >> l >> r;
range[i] = {l, r};
}
sort(range, range + n);
priority_queue<int, vector<int>, greater<int>> heap;//小根堆
for (int i = 0; i < n; i ++ )
{
auto r = range[i];
if (heap.empty() || heap.top() > r.l) heap.push(r.r);
else
{
heap.pop();
heap.push(r.r);
}
}
cout << heap.size() <<endl;
return 0;
}5.股票买卖
- 第一问:从前往后遍历双指针,每次后指针比前指针所指元素小,则前指针赋值为后指针,反之,则计算此时的收益和ans做比较
C++
#include <bits/stdc++.h>
using namespace std;
const int MMM = 10010;
int a[MMM];
int n, ans;
void solve()
{
int i = 1, j = 2;
for(; j <= n; j ++ )
{
if(a[i] > a[j])
{
i = j;
}
else
{
ans = max(ans, a[j] - a[i]);
}
}
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++ )
{
cin >> a[i];
}
solve();
cout << ans << endl;
return 0;
}- 第二问:找上涨区间即可
C++
#include <bits/stdc++.h>
using namespace std;
const int MMM = 10010;
int a[MMM];
int n, ans;
void solve()
{
int i = 1, j = 1;
for(; j <= n; j ++ )
{
if(a[j+1] < a[j])
{
ans = ans + a[j] - a[i];
i = j + 1;
}
}
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++ )
{
cin >> a[i];
}
solve();
cout << ans << endl;
return 0;
}- 进阶:如果手续费需要2
C++
#include <iostream>
#include <vector>
using namespace std;
int maxProfit(vector<int>& prices, int fee)
{
int n = prices.size();
int profit = 0;
int buyPrice = prices[0]; // 初始买入价格设为第一天的价格
for (int i = 1; i < n; ++i) {
// 如果当前价格低于之前的买入价格,则考虑在这一天买入
if (prices[i] < buyPrice)
{
buyPrice = prices[i];
}
// 如果当前价格减去买入价格大于交易费用,则考虑卖出
if (prices[i] > buyPrice + fee)
{
profit += prices[i] - buyPrice - fee; // 计算这次交易的利润
buyPrice = prices[i] - fee; // 更新买入价格为当前价格减去交易费用
// 这一步是为了防止在价格小幅波动时重复交易
}
}
return profit;
}
int main()
{
vector<int> prices = {1, 3, 2, 8, 4, 9};
int fee = 2;
cout << "最大利润: " << maxProfit(prices, fee) << endl;
return 0;
}6.摇摆序列
一个整数序列,如果两个相邻元素的差恰好正负(或负正)交替出现,则该序列称为摇摆序列,一个小于2个元素的序列直接为摇摆序列 。给一个随机序列,求这个序列的最长摇摆子序列长度。
- 算有几个转折点即可
C++
#include<bits/stdc++.h>
using namespace std;
int n;
int wig(vector<int> &nums)
{
if(nums.size() < 2) return nums.size();
static const int BEGIN = 0;
static const int UP = 1;
static const int DOWN = 2; //扫描时候的三种状态
int STATE = BEGIN;
int max_length = 1;//摇摆序列最大长度至少为1,0个和1个元素就返回了,现在至少两个元素
for(int i = 1 ; i < nums.size() ; i++)
{
switch(STATE){ //当前状态-起始状态
case BEGIN:
if(nums[i-1] < nums[i]){ //上升时候
STATE = UP; //状态转移
max_length++;
}else if(nums[i-1] > nums[i]){ //下降时候
STATE = DOWN;
max_length++;
}
break;
case UP:
if(nums[i-1] > nums[i]){
STATE = DOWN;
max_length++;
}
break;
case DOWN:
if(nums[i-1] < nums[i]){
STATE = UP;
max_length++;
}
break;
} //switch
} //for
return max_length;
}
int main()
{
vector<int> v;
cin >> n;
while(n--)
{
int a;
cin >> a;
v.push_back(a);
}
cout<<wig(v);
} 7.多机调度
设有n个独立的作业{1,2,...,n},由m台相同的机器{1,2, ...,m}进行加工处理,作业i所需的处理时间为ti (1≤i≤n),每个作业均可在任何一台机器上加工处理,但未完工前不允许中断,任何作业也不能拆分成更小的子作业。要求给出一种作业调度方案,使所给的 n个作业在尽可能短的时间内由m台机器加工处理完成。(贪心求近似解)
- 每次取最长作业,但是只是近似解
C++
#include<bits/stdc++.h>
using namespace std;
bool compare(int a,int b)
{
return a>b;
}
int main(){
int n,m; //作业个数为n, 机器个数为m
cout<<"请输入作业和机器的个数:"<<endl;
cin>>n>>m;
vector<int> time(n);
vector<int> sumTime(m,0); //0表示初始化值为0
cout<<"请输入每个作业的处理时间:"<<endl;
for(int i=0;i<n;i++)
{
cin>>time[i];
}
sort(time.begin(),time.end(),compare); //对time进行排序,从大到小。
for(int i=0;i<n;i++)
{
int select=0;
for(int j=0;j<m;j++)
{
if(sumTime[j]<sumTime[select])
{
select=j;
}
}
//machine[select].push_back(time[i]);
sumTime[select]=sumTime[select]+time[i];
}
int maxTime=sumTime[0];
for(int j=0;j<m;j++)
{
if(sumTime[j]>maxTime)
{
maxTime=sumTime[j];
}
}
for(int j=0;j<m;j++)
{
cout<<"第"<<j+1<<"台机器所需处理总时间为: "<<sumTime[j]<<endl;
}
cout<<"处理所有作业时间共需: "<<maxTime;
return 0;
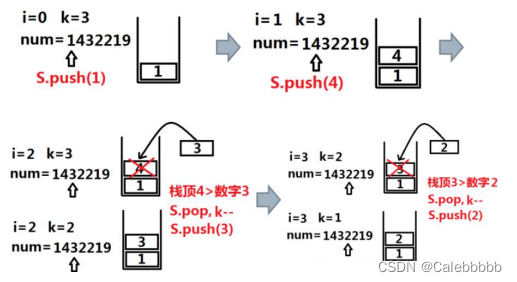
}8.移除k个数字
- 用堆实现,放入元素小于堆顶元素则清除堆顶
- 要注意清除前导0
C++
#include <bits/stdc++.h>
using namespace std;
int main()
{
string num;
int k;
cin>>num>>k;
string res="0"; // 避免处理边界
for(int i=0; i<num.size(); i++)
{
while(k&&res.back()>num[i]) // 处理逆序
{
res.pop_back();
k--;
}
res+=num[i];
}
while(k) res.pop_back(),k--; // 如果还剩余k,将后面删掉
int i=0;
while(i<res.size()&&res[i]=='0') i++; // 定位 去掉前导零的位置
if(i==res.size()) cout<<"0"<<endl;
else cout<<res.substr(i)<<endl;
return 0;
}9.跳跃游戏
- 思路:

- 其实就是从前往后遍历,不断取最大能及距离,判断是否可以抵达最终点即可
C++
#include <bits/stdc++.h>
using namespace std;
bool canJump(vector<int>& nums)
{
int max_len = 0;//最远可到达长度
int len = 0;//遍历当前下标元素可到达的长度
int sign = 0;//标志符
//判断数组长度
if (nums.size() == 1) {
return true;
} else {
//遇到0时,进行判断
for (int i = 0; i < nums.size(); i++) {
if (nums[i] == 0) {
if (max_len <= i) {
sign = 1;
break;
}
}
//更新max_len
len = i + nums[i];
if (len > max_len) {
max_len = len;
if (max_len >= nums.size()-1) {
break;
}
}
}
//最后根据标识符判断结果
if (sign == 0) {
return true;
} else {
return false;
}
}
}
int main()
{
vector<int> a;
int n;
cin >> n;
while(n -- )
{
int i;
cin >> i;
a.push_back(i);
}
bool b = canJump(a);
if(b) cout << "true" << endl;
else cout << "false" << endl;
return 0;
}