自适应Q的容积卡尔曼滤波MATLAB例程|完整代码

Evand J2024-06-04 17:48

前言

给出自适应容积卡尔曼滤波（ACKF）的MATLAB代码。

主要思想

通过自适应状态协方差Q来实现，得到了比传统方法更低的估计误差。适用于Q无法获取、估计不准、变化不定的情况，只有一个M文件，方便运行，保运行成功，不包讲解。

运行截图

三轴状态的估计曲线：

状态误差的曲线如下：

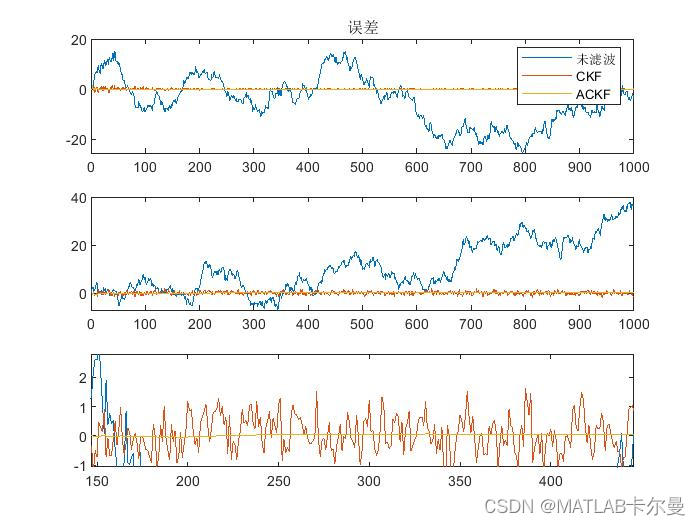
因为未滤波的误差太大了，将中间红色和黄色部分放大一点，得到下图：

能明显看出来ACKF的误差更小。

同时，程序还输出了误差的CDF图像，供参考：

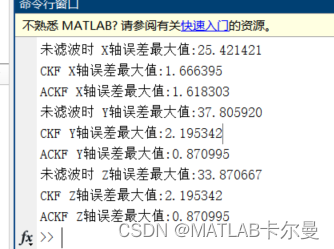
误差的统计特性如下：

代码结构

代码文件由以下几个部分组成：

源代码

matlab 复制代码

% CKF与ACKF效果对比，自适应调节Q
% Evand©2024
% 作者联系方式：evandjiang@qq.com（除前期达成一致外，付费咨询）
% 2024-5-30/Ver1/
clear;clc;close all;
rng(0);
%% 滤波模型初始化
t = 1:1:1000;
Q0 = 1*diag([1,1,1]);w=sqrt(Q0)*randn(size(Q0,1),length(t));
R0 = 1*diag([1,1,1]);v=sqrt(R0)*randn(size(R0,1),length(t));
P0 = 1*eye(3);
X=zeros(3,length(t));
X_ekf=zeros(3,length(t));
X_ekf(:,1)=X(:,1);
Z=zeros(3,length(t)); %定义观测值形式
Z(:,1)=[X(1,1)^2/20;X(2,1);X(3,1)]+v(:,1); %观测量
%% 运动模型
X_=zeros(3,length(t));
X_(:,1)=X(:,1);
for i1 = 2:length(t)
    X(:,i1) = [X(1,i1-1) + (2.5 * X(1,i1-1) / (1 + X(1,i1-1).^2)) + 8 * cos(1.2*(i1-1));
        X(2,i1-1)+1;
        X(3,i1-1)]; %真实值
    X_(:,i1) = [X_(1,i1-1) + (2.5 * X_(1,i1-1) / (1 + X_(1,i1-1).^2)) + 8 * cos(1.2*(i1-1));
        X_(2,i1-1)+1;
        X_(3,i1-1)] + w(:,i1-1);%未滤波的值
    Z(:,i1) = [X(1,i1).^2 / 20;X(2,i1);X(3,i1)] + v(i1); %观测值
end

%% CKF
Q = Q0*2; %人工构造Q不准确的情况
% 完整代码下载链接：https://gf.bilibili.com/item/detail/1105551012
R = R0;
P = P0;