前言
在上一章我们讲了二叉树，这一节我们来讲堆（优先级队列），所以想知道堆创建，可以看一下二叉树的一些简单概念。http://t.csdnimg.cn/4jUR6
http://t.csdnimg.cn/4jUR6
目录
堆
1.概念
我们知道队列是一种先进先出的数据结构，但是在某些情况下，操作的数据可能带有优先级，出队的时候，可能需要优先级较高的元素出队列。
所以，数据结构应该提供两个最基本的操作，一个是返回最高优先级对象 ，二是添加新的对象 。这种数据结构就是优先级队列（Priority Queue）。
2.优先级队列的模拟实现
2.1堆的概念
如果有一个集合K=｛0,k1,,k2,...,kn-1｝,把集合K的元素按照完全二叉树的顺序存储方式 存储在一个一维数组中，并且满足：K(i)<=K(2I+1)且K(i)<=K(2i+2) (K(i)>=K(2I+1)且K(i)>=K(2i+2) ),i=0,1,2,3... ,则叫做小堆（或大堆）。
将根节点最小的堆叫做小根堆或最小堆。
将根节点最大的堆叫做大根堆或最大堆。
2.2堆的性质
1.堆中的某个节点总是不大于或不小于其父节点的值。
2.堆总是一棵完全二叉树。
在jDK1.8中的优先级队列底层使用了堆这种数据结构，而堆其实就是就是完全二叉树的基础进行调整的。
2.3堆的存储方式
我们从堆的概念可以知道，堆是一棵完全二叉树，所以可以层序的规则采用顺序的方式存储。
注意：对于非完全二叉树，不适合采用顺序方式进行存储。
原因：为了还原二叉树，空间中必须要存储空节点，就会导致空间利用率较低。
将元素存储到数组中后，我们可以根据二叉树的性质5进行还原，假设i为节点在数组中的下标，则有：
- 如果i为0，则i表示的节点为根节点，否则i节点的双亲节点为（i-1）/2;
- 如果2*i+1小于节点个数，则**节点i的左孩子下标为2*i+1,**否则没有左孩子；
- 如果2*i+2小于节点个数，则节点的右孩子下标为2*i+2,否则没有右孩子。
2.4堆的创建
2.4.1向下调整
我们拿集合｛28,16,48,13,46,45,25,36,22,42｝为例，如何将其创建成堆呢？？
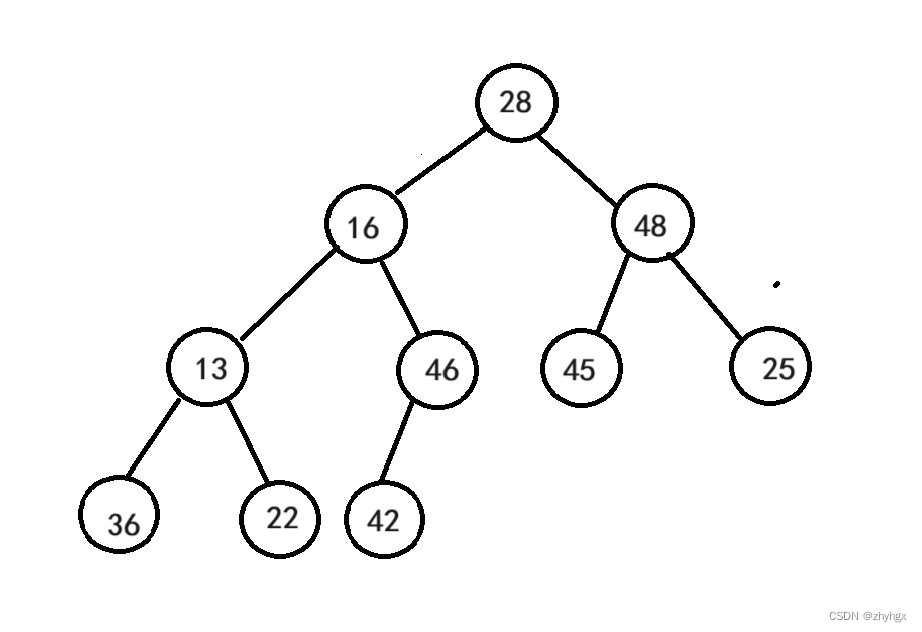
我们可以看到，此时根节点的左右子树都不满足堆的性质。所以我们需要对每个有子树的父节点进行向下调整。
1.向下调整思路
对于一棵完全二叉树，要其变成小根堆（或大根堆），我们需要满足根节点的左右子树都是小堆（大堆）。
规则：1.找出父亲节点的左右节点中值较小（或较大）的节点。
2.找出较小值（较大值）与父亲节点进行比较。
3.小堆：若父亲节点比左右节点中的较小值大，则进行交换，再将较小值的位置给到父亲节点，再进行向下调整。当父亲节点的值小于左右节点中的较小值时，调整停止
大堆：若父亲节点比左右节点中的较大值小，则进行交换，再将较大值的位置给到父亲节点，再进行向下调整。当父亲节点的值小于左右节点中的较小值时，调整停止
我们以创建小根堆为例：
对于上图中的二叉树，我们可以看到其左右子树并不是小堆。
所以我们需要先对其左右子树进行向下调整：
我们从根节点位置最大的一个开始，依次递归进行调整。
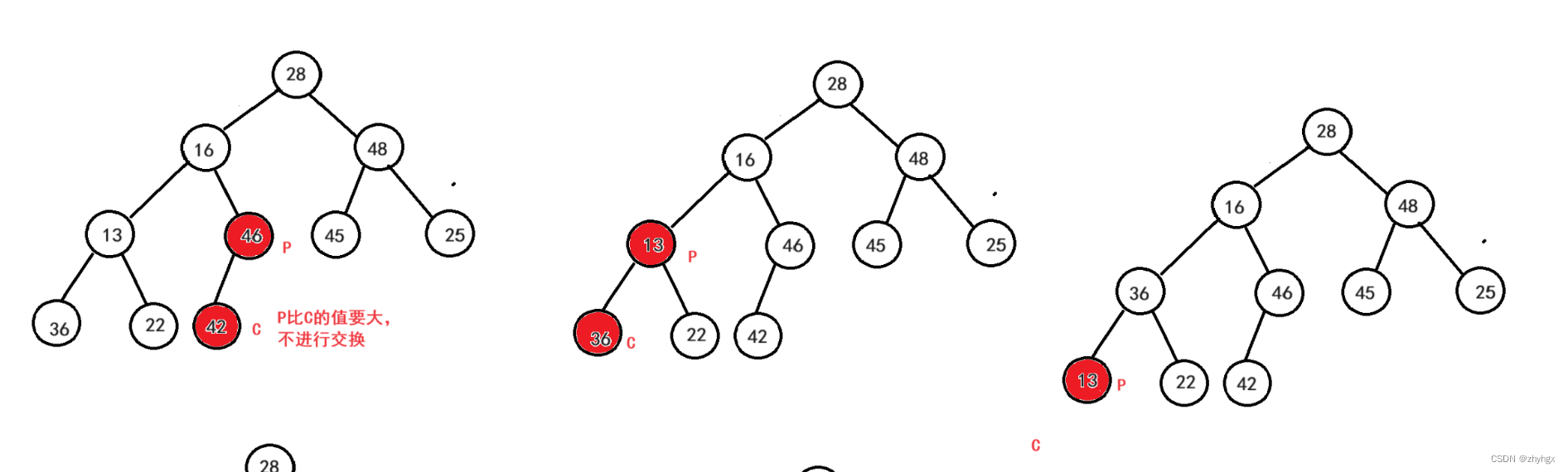
我们可以看到父亲节点（46）比孩子节点（42）要大，所以要进行交换。
再让父亲节点（P）走向孩子节点（C）的位置，但是由于此时父亲节点并没有孩子节点，停止调整。再让P从节点值为13的位置开始向下调整，此时由于左右节点值都大于13，满足堆的性质，不进行交换。
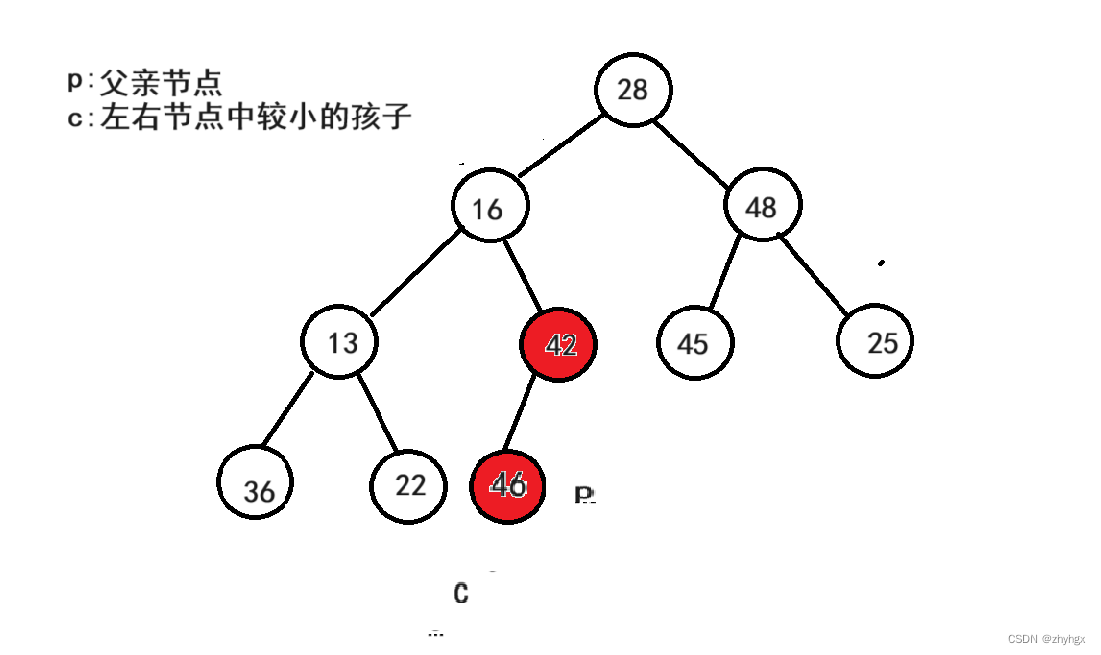
依次类推：
当P走到节点值为48的位置时，再与左右孩子中的最小值进行比较，进行互换。
当P走到父亲节点（16）的位置时，进行向下调整，再让P往下走，但此时P所处的节点其满足堆的性质，不进行互换，调整停止。
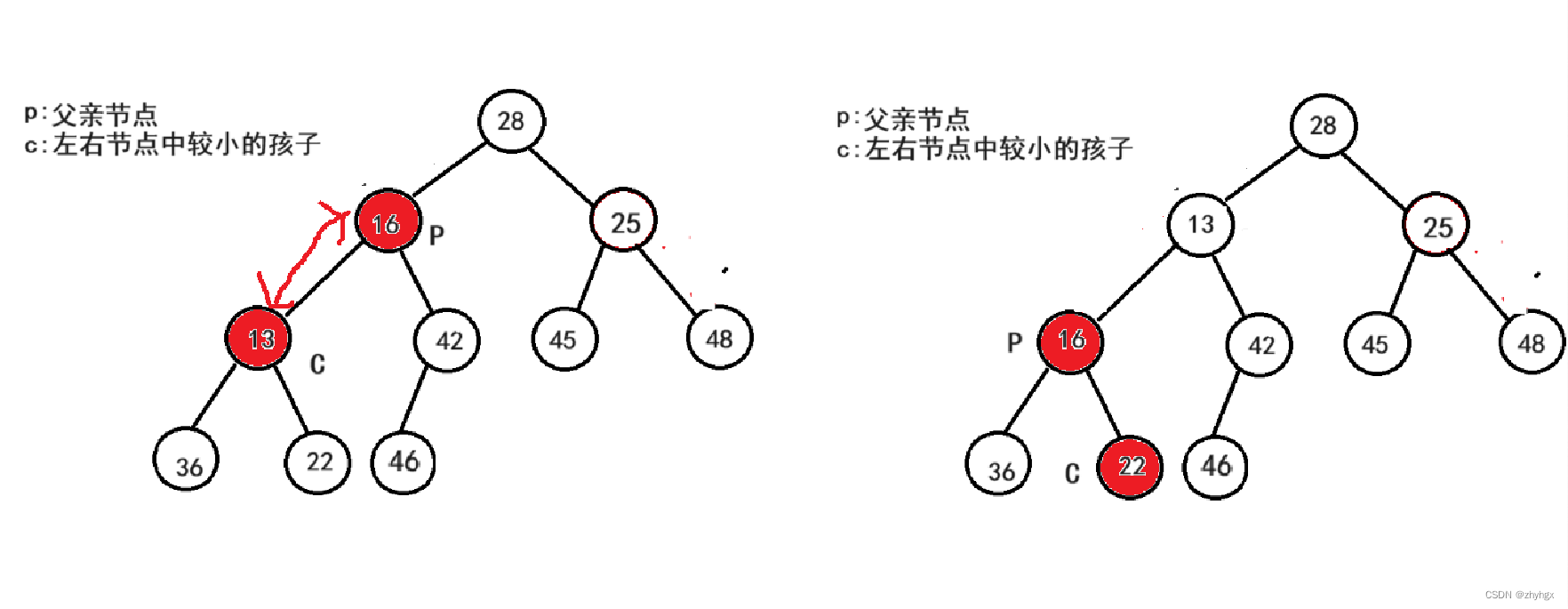
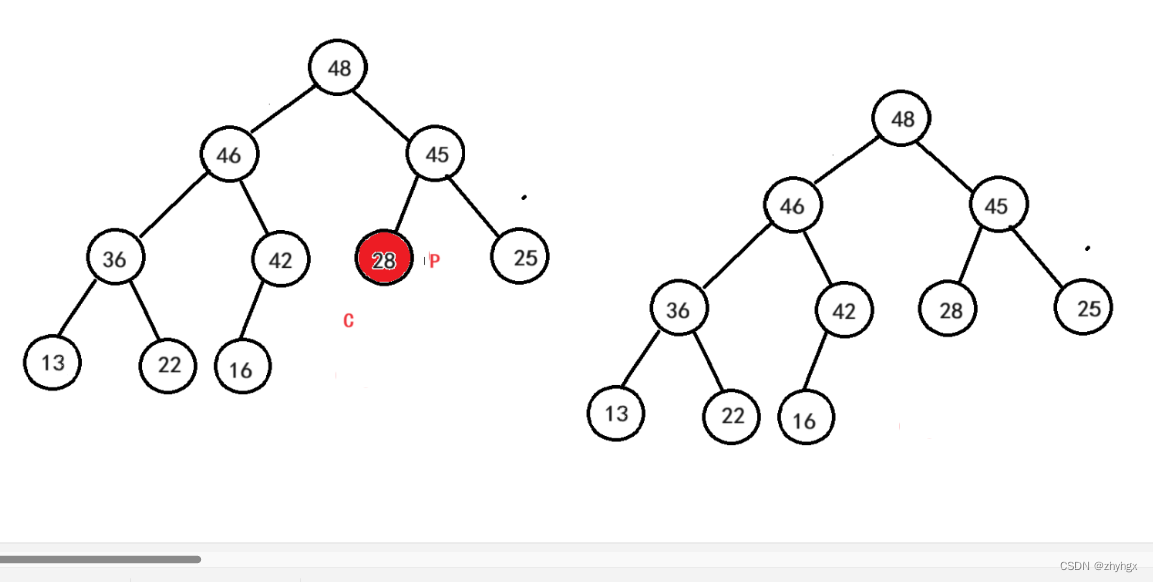
此时，根节点（28）的左右子树都已经满足堆的性质，现只需要对根节点进行向下调整，就可以得到一个小根堆。
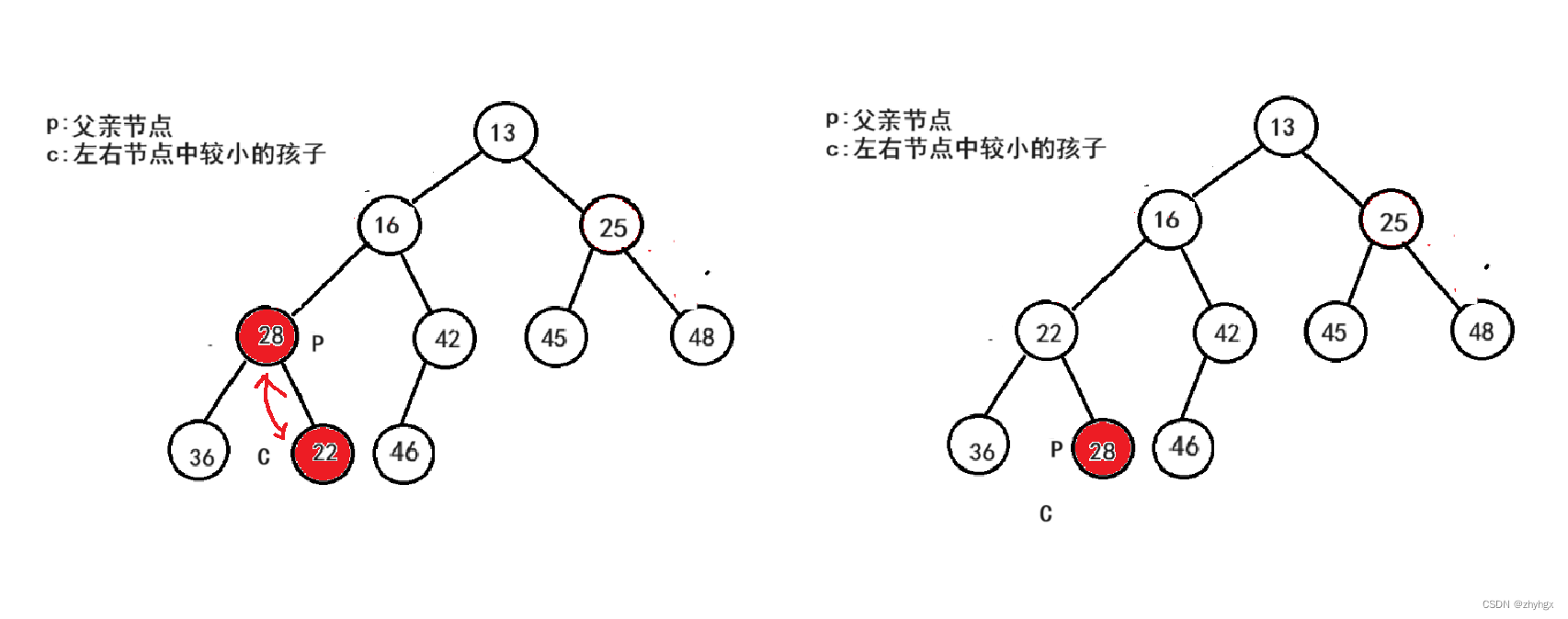
至此，我们就得到一个小根堆。
我们如果要创建一个大根堆，思路也是与创建小根堆的思路一样，只是在交换值时，是交换孩子节点中的较大值。
2.代码实现
对于上面我们所推的，
其小根堆为{13，16，25，22，42，45，48，36，28，46}；
其大根堆为{48，46，45，36，42，28，25，13，22，26｝；
java
package MyQueue;
/**
* Pheap类实现了大根堆数据结构。
*/
class Pheap {
public int[] elem; // 存储堆元素的数组
public int useSize; // 当前堆中元素的使用大小
/**
* 构造函数，初始化堆数组。
*
* @param size 堆数组的初始大小
*/
public Pheap(int size){
this.elem=new int[size];
}
/**
* 使用给定数组初始化堆。
*
* @param arr 用于初始化堆的数组
*/
public void init(int[] arr){
for(int i=0;i<arr.length;i++){
this.elem[i]=arr[i];
}
useSize=arr.length;
}
/**
* 交换数组中两个元素的位置。
*
* @param child 需要交换的子元素下标
* @param parent 需要交换的父元素下标
*/
public void swap(int child,int parent){
int temp=elem[child];
elem[child]=elem[parent];
elem[parent]=temp;
}
/**
* 向下调整以维护大根堆性质。
*
* @param parent 需要向下调整的父节点下标
* @param end 堆数组的结束下标
*/
public void sitDownBig(int parent,int end){
int child=2*parent+1;
while(child<end){
if(child+1<end&&elem[child]<elem[child+1]){
child++;
}
if(elem[child]>elem[parent]){
swap(child,parent);
parent=child;
child=2*parent+1;
}else{
break;
}
}
}
/**
* 构建大根堆。
*/
public void createHeapBig(){
for(int parent=(useSize-1-1)/2;parent>=0;parent--){
sitDownBig(parent,useSize);
}
}
/**
*构建小根堆
*/
public void creatHeapSmall(){
for(int parent=(useSize-1-1)/2;parent>=0;parent--){
sitDownSmall(parent,useSize);
}
}
/**
* 将指定元素下沉以维护堆的性质。该方法用于调整二叉堆，确保从指定父节点到末尾子节点的子树满足堆的性质。
*
* @param parent 父节点的索引
* @param end 堆数组的末尾索引
*/
public void sitDownSmall(int parent, int end) {
// 计算左子节点的索引
int child = 2 * parent + 1;
while (child < end) {
// 如果存在右子节点，并且右子节点比左子节点大，则将当前 child 指针指向右子节点
if (child + 1 < end && elem[child] > elem[child + 1]) {
child++;
}
// 如果当前 child 节点的值小于父节点的值，则交换它们，并将 parent 更新为当前 child，继续下沉调整
if (elem[child] < elem[parent]) {
swap(child, parent);
parent = child;
// 更新 child 为新的左子节点索引
child = 2 * parent + 1;
} else {
// 如果当前 child 节点的值不小于父节点的值，说明已满足堆的性质，结束调整
break;
}
}
}
}测试一下
java
public class Prioirtyq {
public static void main(String[] args){
Pheap p=new Pheap(10);
int arr[]={28,16,48,13,46,45,25,36,22,42};
p.init(arr);
p.creatHeapSmall();
Pheap p1=new Pheap(10);
p1.init(arr);
p1.createHeapBig();
}
}
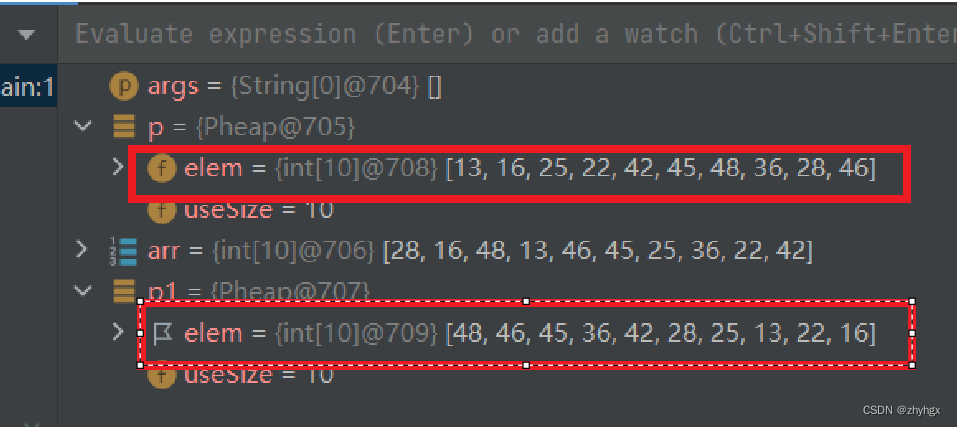
可以看到，确实是所推的那样。
3.建堆的时间复杂度
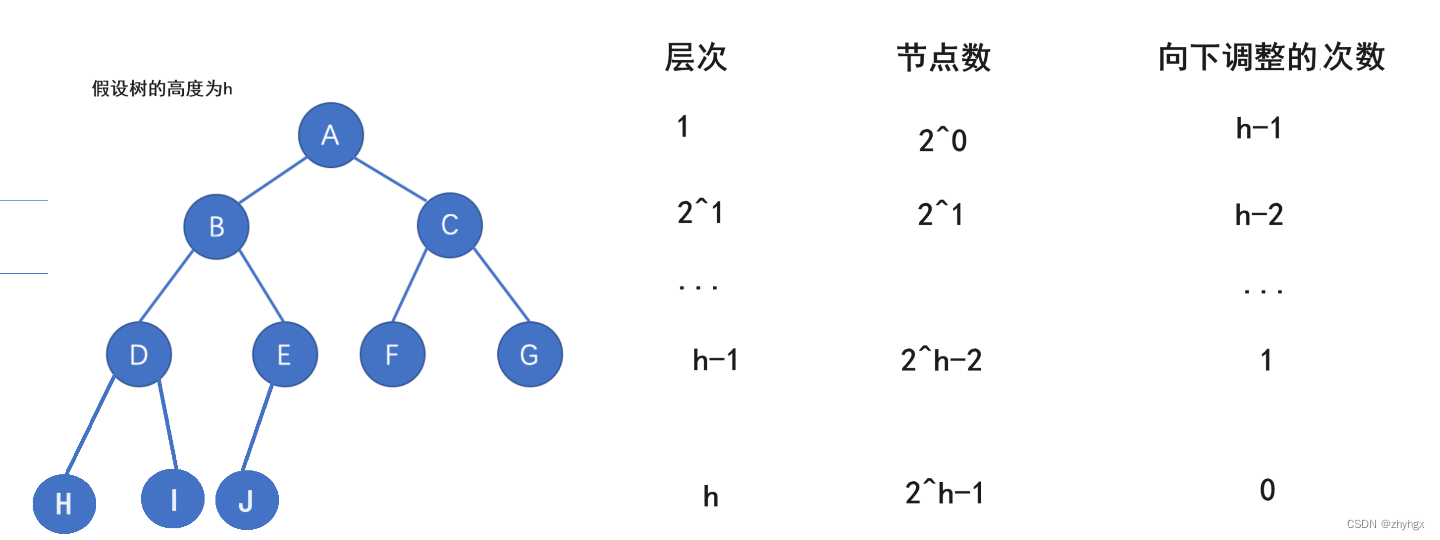
我们假设完全二叉树的高度为h，
那么，对于第一层，其结点只有一个，但是其需要向下调整h-1层。对于第二层，其节点有2^1个，每个结点需要向下调整的次数为h-2，以此类推，对于第h-1层，其拥有的节点有2^{h-2}个，但其属于倒数第二层，所以只需要向下调整1次。
那么对于一棵完全二叉树，要想将其建成一个堆，其时间复杂度就是每层的节点数*其向下调整的次数所需要花费的时间。
T(n)=2^0*(h-1)+2^1*（h-2）+2^2*(h-3)+...+2^(h-2)*1 (1)式
我们不难看出，这是一个等差✖等比求和公式，我们可以用错位相减法来求出T(n)，不难看出，其公比为2.
所以在（1）式左右两边同时✖2，得
2T(n)= 2^1*(h-1)+2^2*(h-2)+2^3*(h-3)+...+2^(h-1)*1 (2)式
（2）式-（1）式可得
T(n)=2^1+2^2+2^3+...+2^(h-1)+1-h
我们将1化为2^0,
T(n)=2^0+2^1+2^2+2^3+...+2^(h-1)-h
可以看出这是一个等比数列求和公式，根据求和公式Sn=a1*(1-q^n)/1-q,得
T(n)=1*(1-2^h)/(1-2)-h=2^h-1-h
由二叉树的性质我们可以得到
节点数N=2^h-1
树的高度h=log2(N+1)
带入得
T(n)=N-log2(N+1)
根据大O渐进表示法
T(n)=O(N)
所以我们建堆的时间复杂度为O(N).
向下调整的时间复杂度为O(logN）.
2.5堆的插入
在一个堆中，如果我们想插入一个数据，那么就在堆尾进行插入，再进行向上调整.
我们同时也需要考虑此时堆满了没
2.5.1向上调整
思路：对于插入的节点（我们称作目标节点）
1.将目标节点与其父亲节点进行比较。
大根堆：如果是大根堆，当父亲节点比目标节点小，那就目标节点和父亲节点进行互换后，将父亲节点的位置给到目标节点，接着继续进行向上调整。当父亲节点比目标节点大，停止向上调整。
小根堆：当父亲节点比目标节点大，那就目标节点和父亲节点进行互换后，将父亲节点的位置给到目标节点，接着继续进行向上调整。当父亲节点比目标节点小，停止向上调整。
我们以小根堆插入新节点为例：
我们用上述中所创建而成的小根堆，让其插入一个值为10的节点，如图
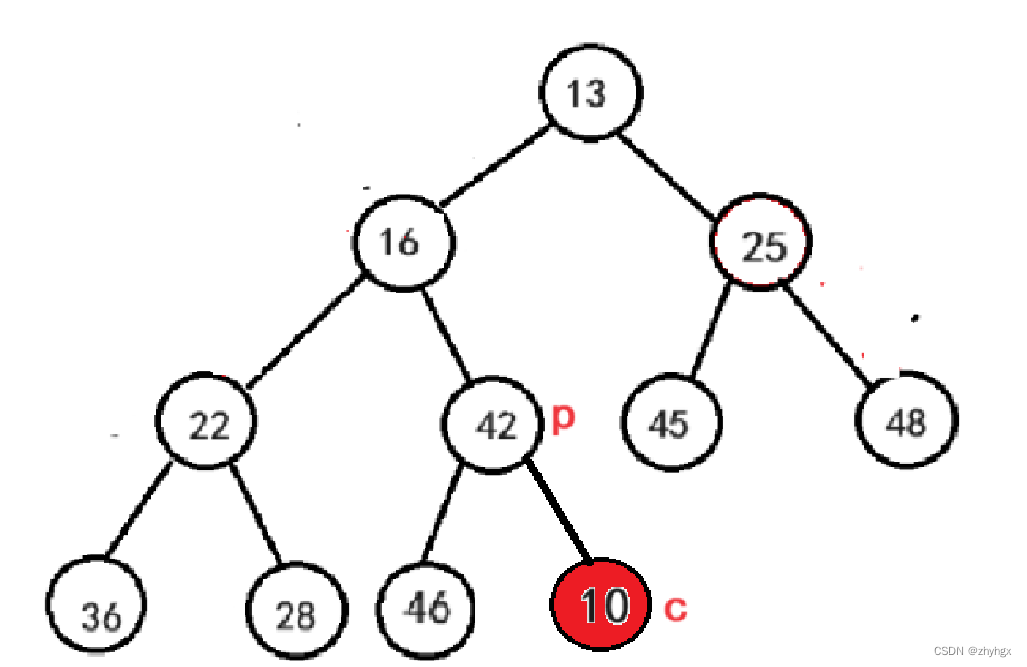
我们可以知道，新插入的节点其父亲节点是值为42的节点，明显比值为10目标节点要大，所以要进行互换，再进行向上调整。
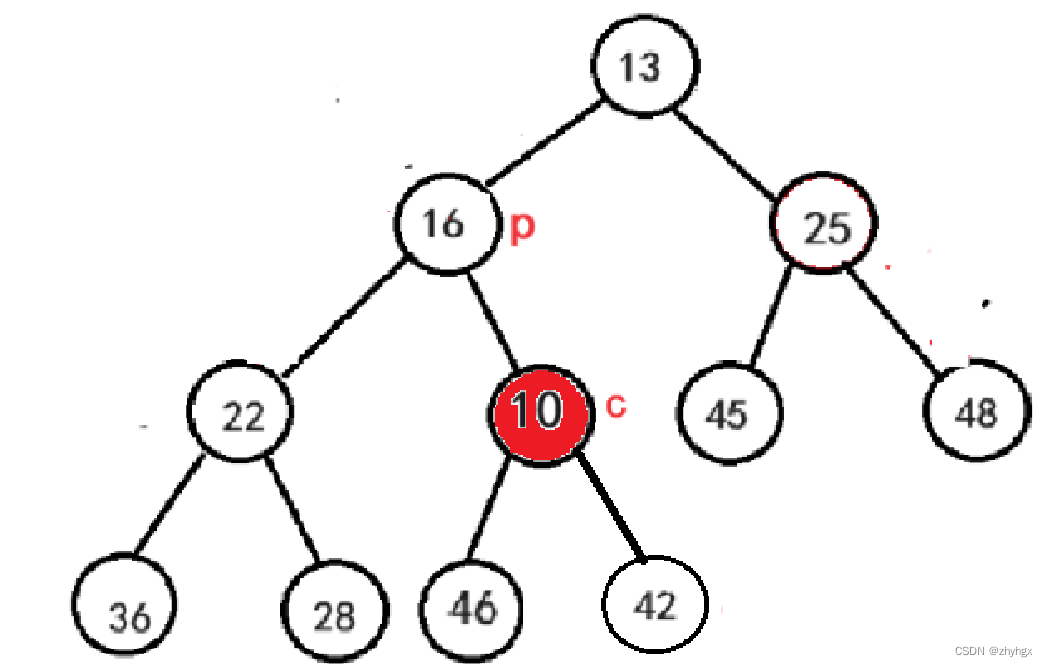
最后我们可以得到：
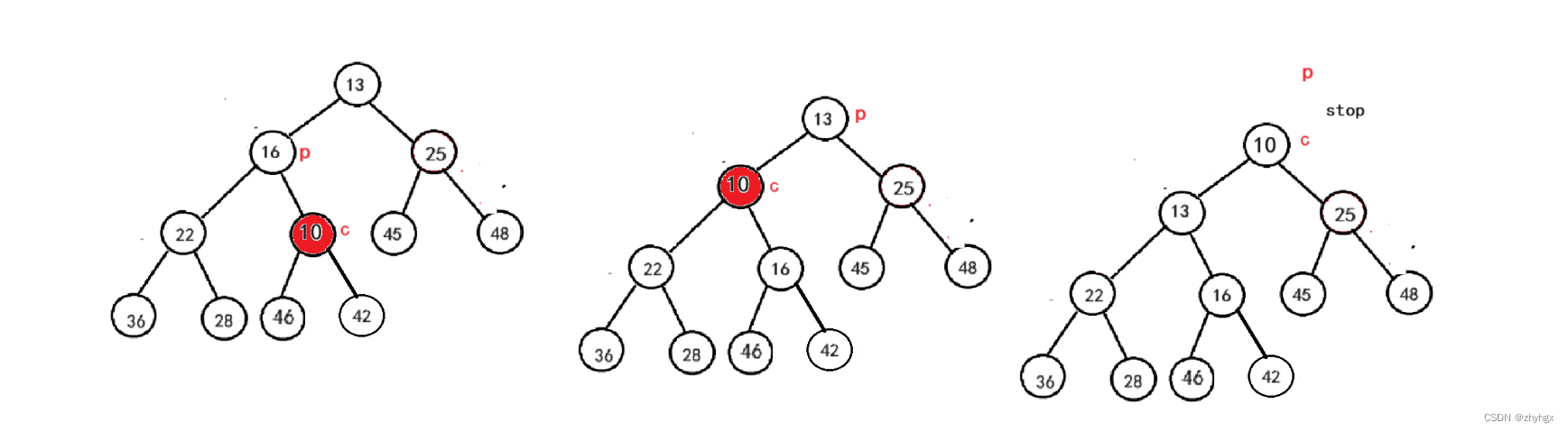此时小根堆为｛10，13，25，22，16，45，48，36，46，42｝。
2.5.2堆插入代码实现：
java
public void pushInS(int val){
// 判断堆是否已满
if(isFull()){
elem= Arrays.copyOf(elem,elem.length*2);
}
//进行插入
elem[useSize++]=val;
//进行向上调整
sitUp(useSize-1);
}
public void sitUp(int child){
int parent=(child-1)/2;
while(child>=0){
if(elem[child]<elem[parent]){
swap(child,parent);
child=parent;
parent=(child-1)/2;
}else{
break;
}
}
}
/**
* 检查堆是否已满。
*
* @return 堆是否已满的布尔值
*/
public boolean isFull(){
return useSize==elem.length;
}
可以看到，确定是所推断的那样。
2.6堆元素的删除
堆元素的删除一定是删除的堆顶元素！！！
2.6.1思路
对顶元素的删除其实也是利用到向下调整。
1.将对顶元素与队尾的元素进行互换
2.让有效个数减1
3.再来一次向下调整
2.6.2.代码实现
java
public int Delete(){
if(isEmpty()){
throw new RuntimeException("堆为空");
}
int val=elem[0];
swap(0,useSize-1);
useSize--;
sitDownSmall(0,useSize);
return val;
}2.7获取堆的元素个数&&获取堆顶元素&&堆的打印
java
public int size(){
return useSize;
}
public int peek(){
if(isEmpty()){
throw new RuntimeException("堆为空");
}
return elem[0];
}
public void print(){
for(int i=0;i<useSize;i++){
System.out.print(elem[i]+" ");
}
System.out.println();
}3.常用接口特性
3.1PriorityQueue的特性
在java集合框架中，提供了PriorityQueue和PriorityBlockingQueue 两种类型的优先级队列，但是PriorityQueue时线程不安全的，而PriorityBlockingQueue是线程安全的。
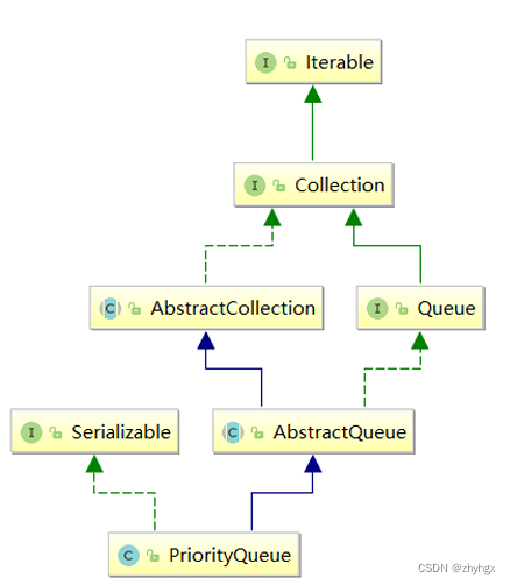
我们在使用PriorityQueue时，需要导入相应的包
import java.util.PriorityQueue;
注意：
1.PriorityQueue中放置的元素必须要能够比较大小，不能插入无法比较大小的对象，否则会抛出 ClassCastException异常
不能插入null对象，否则会抛出NullPointerException
没有容量限制，可以插入任意多个元素，其内部可以自动扩容
插入和删除元素的时间复杂度为O(log2N).
PriorityQueue底层使用了堆数据结构
PriorityQueue默认情况下是小堆---即每次获取到的元素都是最小的元素
3.2PriorityQueue常用接口介绍
1.优先级队列的构造
常用的有以下几个：
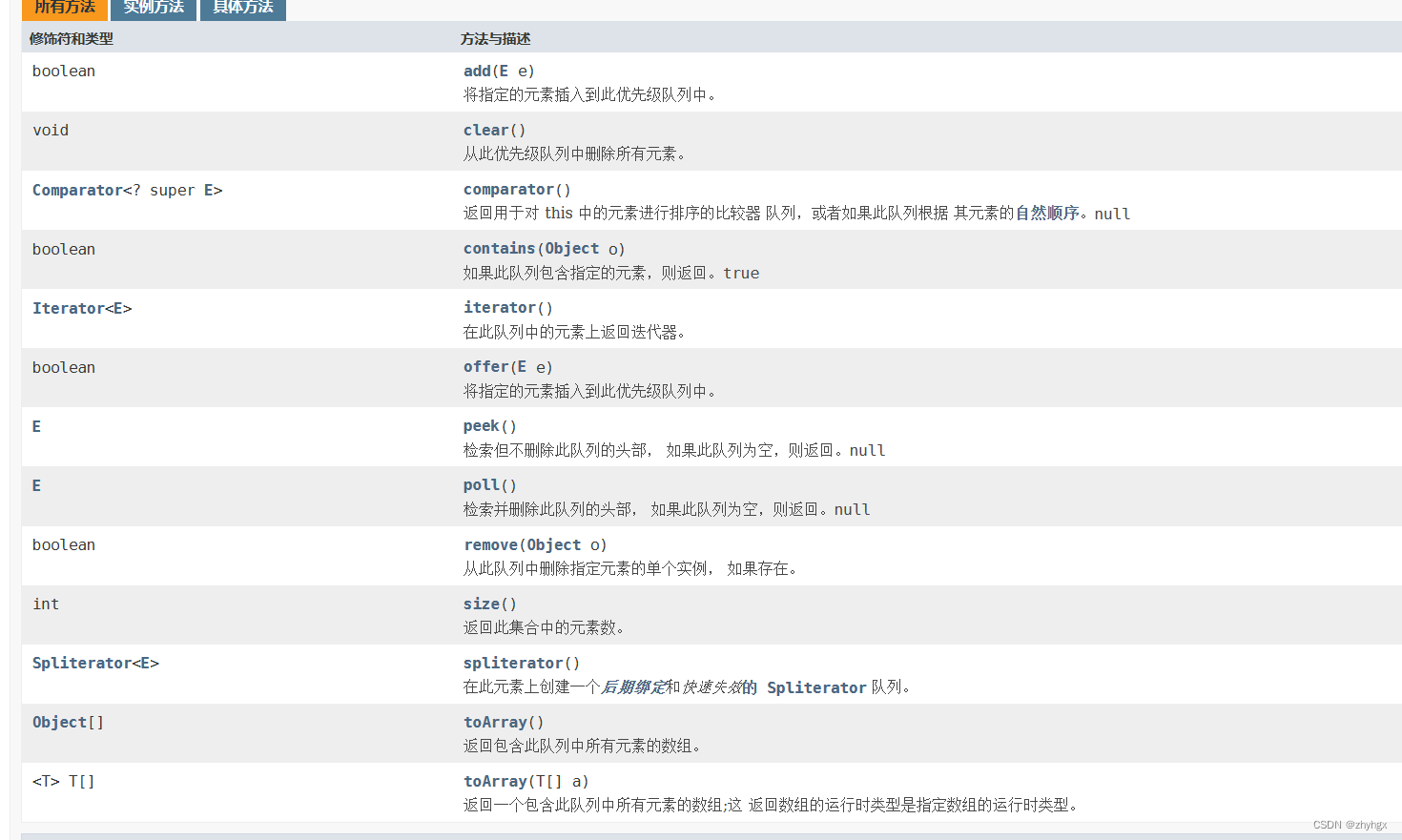如果想要了解更多关于优先级队列，可以点击PriorityQueue （Java 平台 SE 8 ） (oracle.com)
java
public static void main(String[] args){
PriorityQueue<Integer> pq=new PriorityQueue<>();
pq.offer(1);
pq.offer(2);
pq.offer(3);
System.out.println(pq.poll());
System.out.println(pq.peek());
}扩容规则：
如果容量小于64时，是按照oldCapacity的2倍方式扩容的
如果容量大于等于64，是按照oldCapacity的1.5倍方式扩容的
如果容量超过MAX_ARRAY_SIZE，按照MAX_ARRAY_SIZE来进行扩容。
数据结构的堆就先到这。
若有不足之处，欢迎指正~~