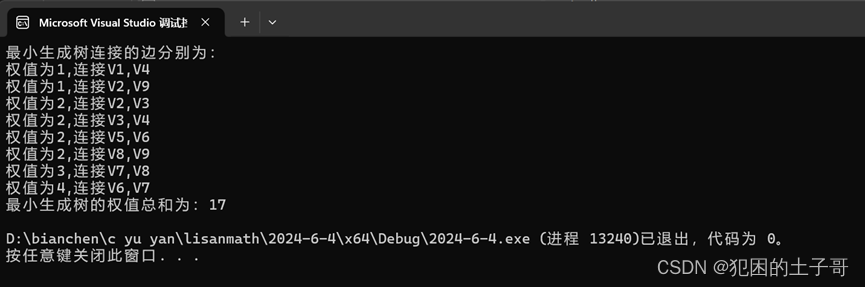
Kruskal算法求出最小生成树。
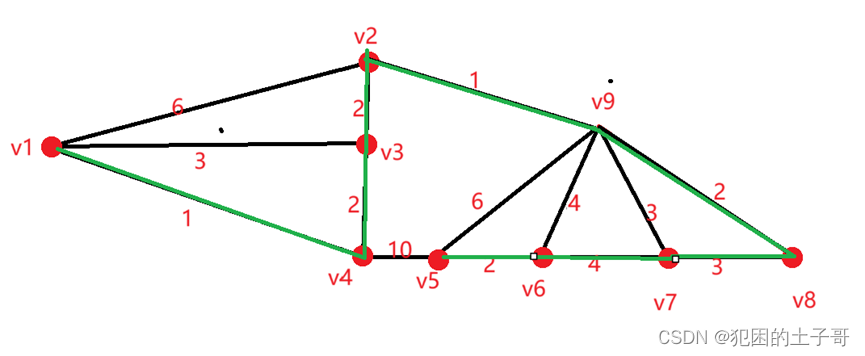
图形
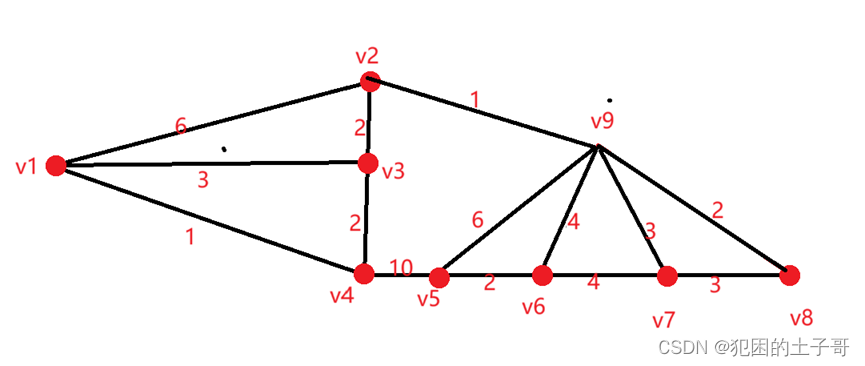
算法描述
先找最小权值边为1的边有(V1,V4),(V2,V9),保证不产生回路就可以成功选择边
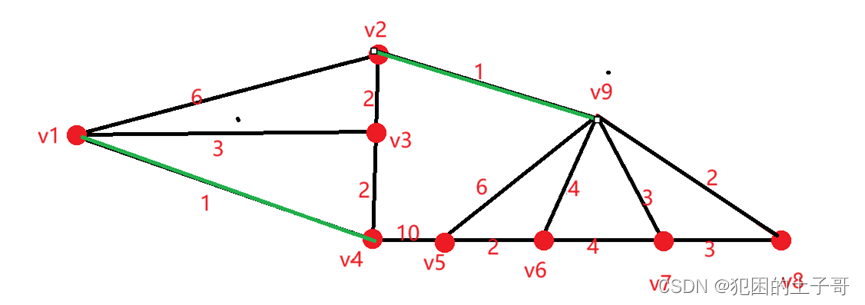
除去上一次找的边后,在找权值最小的边为2的有(V2,V3),(V4,V3),(V5,V6),(V9,V8),连接不产生回路的边
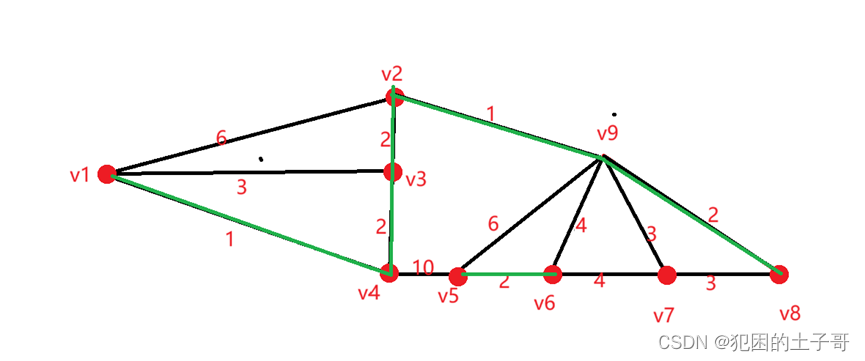
除去之前找过的边,后面再看权值最小的边为3的边有(V1,V3),(V7,V8),(V9,V7)
按顺序判断(V1,V3)边会产生回路排除,(V7,V8)可选边,当连接完(V7,V8)后判断(V9,V7)连接会造成回路排除

排除找过的边后,找下一个权值最小的为4的边有(V6,V7),(V9,V6)
顺序判断,( V6,V7)符合,连接完(V9,V6)判断连接(V9,V6)是回路不符合
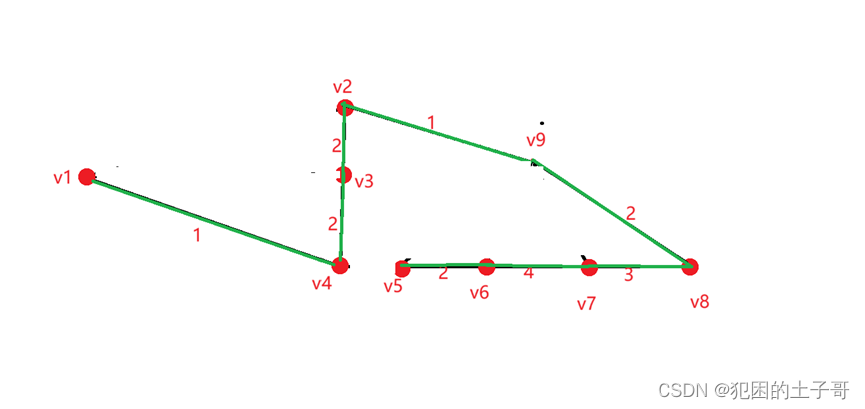
完成所以点相连结束
有N个点,最小生成树有N-1个边
C语言Kruskal算法实现
c
//C语言Kruskal算法实现
#include<stdio.h>
#define M 1000//M表示无穷用1000代替
#define N 9 //N行N列的矩阵
void loop(int arr[N][N],int dot,int c[N])
{
int i;
for ( i = 0; i < N; i++)
{
if (arr[dot][i] == 1)
c[i] = i + 1;
}
}
//标记和判断是否为回路,不是回路返回1,是回路反回0
int Is(int arr[N][N], int row, int column)
{
if (arr[row][column] == 0 || arr[column][row] == 0)
{
int a[N] = { 0 };
int b[N] = { 0 };
loop(arr, row, a);
loop(arr, column, b);
int flag = 1;
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
if (a[i] == b[j] && a[i] !=0)
flag = 0;
}
}
//没产生回路标记1
if(flag)
{
arr[row][column] = 1;
arr[column][row] = 1;
return 1;
}
//产生回路标记-1
else
{
arr[row][column] = -1;
arr[column][row] = -1;
}
}
return 0;
}
int main()
{
//把上图权值对应值写成邻接阵
int map[N][N] =
{
{M,6,3,1,M,M,M,M,M},
{6,M,2,M,M,M,M,M,1},
{3,2,M,2,M,M,M,M,M},
{1,M,2,M,10,M,M,M,M},
{M,M,M,10,M,2,M,M,6},
{M,M,M,M,2,M,4,M,4},
{M,M,M,M,M,4,M,3,3},
{M,M,M,M,M,M,3,M,2},
{M,1,M,M,6,4,3,2,M}
};
int arr[N][N] = { 0 };//用来标记边
int count = 0;//用来记录边的数量,最小生成树的边为数N-1
int i = 0, j = 0;
int min = M;//记录最小权值
int value = 0;//当前要找的最小权值
int sum = 0;//记录总权值
//打印
printf("最小生成树连接的边分别为:\n");
while (1)
{
min = M;//每次把最小权设置为最大
//找权值最小边,和最小权值边的数量
for (i = 0; i < N; i++)
{
for (j = 0; j < N; j++)
{
if (map[i][j] < min && map[i][j] > value)//判断是否为最小权
{
min = map[i][j];
}
}
}
value = min;
//根据前面循环得到最小权值边,标记不构成回路的边
for (i = 0; i < N; i++)
{
for (j = 0; j < N; j++)
{
if (map[i][j] == min && Is(arr, i, j))
{
//打印
printf("权值为%d,连接V%d,V%d\n", value, i + 1, j + 1);
sum += min;
count++;
if (count == (N - 1))
break;
}
}
if (count == (N - 1))
break;
}
//找够边数跳出循环
if (count == (N - 1))
break;
}
printf("最小生成树的权值总和为:%d\n",sum);
return 0;
}