一、并查集
并查集是一种树型的数据结构 ,用来处理不相交集合的元素合并和查询问题。
思想:用一个数组表示整片森林,每棵树的根节点标识该集合,只要找到某个元素对应的树根,就能确定它的集合。
二、并查集的相关操作
首先用一个数组 Parent [ ] 记录每个节点对应的父节点 ,Parent [ i ] 表示 i 的父节点**。**
1.初始化
每个节点都没有与其他的节点相连(构成集合),即每个节点都是所在集合的根节点,
for (int i=1;i<=n;i++) Parent[i]=i;2.查找Find
查询某元素所在集合的根节点。
操作过程:对于一个集合,通过不断的迭代 Parent 数组,直至找到 的节点
int find(int x) //查找x的根节点
{
while(parent[x]!=x) // x 的父亲不是自己(不是根节点)
x=parent[x]; // 迭代向上寻找
return x;
}
3.合并Union
将两个子集合并成一个集合。
操作过程:
①将两个元素(x,y)所在的集合合并,需要通过 Find 函数找到两个元素对应的根节点;
②如果两个根节点相同(即在同一集合内),不需要合并,若两根节点不相同,选择其中一个根节点作为另一个节点的父亲,合并成一个新集合。
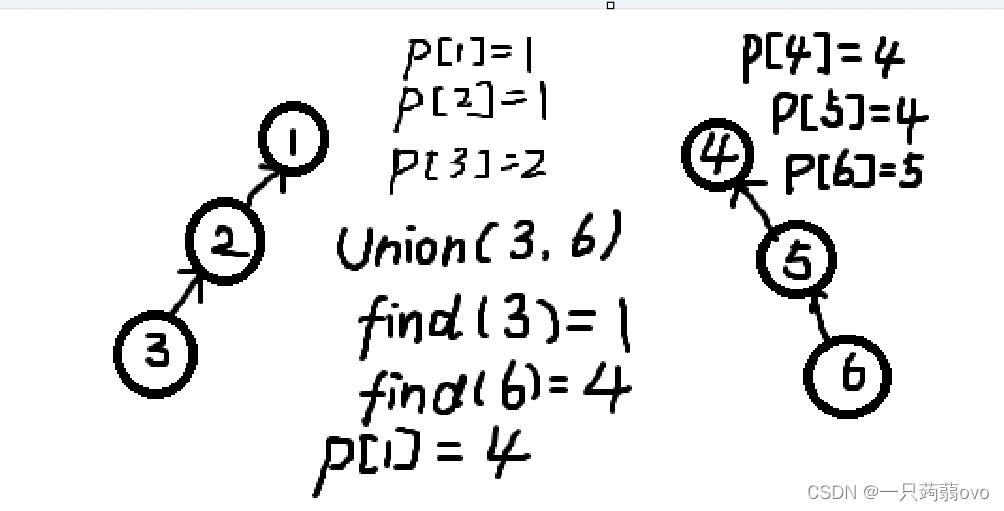
合并后:

void union(int x,int y) //合并 x y 所在集合
{
int fx=find(x),fy=find(y); //找到两个节点对应的根节点
if(fx!=fy) // 不在一个集合中
parent[fx]=fy; // fy 作为 fx 的父节点
}三、并查集的优化
1.路径压缩(优化 Find() 函数)
在合并 Union 操作中,通过以下操作将两个集合合并,即将 节点 fx 接在 节点 fy 后。
if(fx!=fy) parent[fx]=fy;
通常情况下,数据过大导致不断合并,会存在多种情况,最终的树状结构无法预计,即有可能是均匀 n 叉树,也有可能是单支树结构 。当树型结构为单支树,Find() 函数中,每次寻找树根节点都要不断向上搜索,此时效率大大降低 复杂度为 O(n)。
通过路径压缩,直接将每个节点都指向树根节点,这样大大降低时间消耗,只需要递归一次即可找到树根节点。

代码实现:
将单支树转化成路径压缩后,只需要 Find函数 不断向上递归的过程中 更新parent数组,即将路径上点的parent数组全部更新为根节点。
int find(int x) //查找x的根节点
{
if(parent[x]==x) return x; // 根节点
return parent[x]=find(parent[x]); // 向上递归
}2.按秩合并(以树高举例)
在Union操作中,以两个根节点的树高 来判断两点哪点为父节点,为了使树更加均衡,通常将树高更大的点作为父节点,如下图所示。
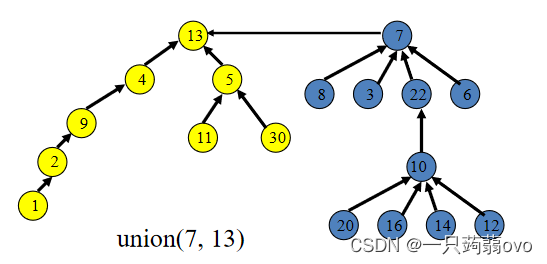
实现:使用 rank() 数组记录树高
当 rank[fx]<rank[fy],则 parent[fx]=fy
当 rank[fx]==rank[fy],则两点均可作为对方的父节点,这里以 parent[fx]=fy 为例,并且将 rank[fy]++
当 rank[fx]>rank[fy],则 parent[fy]=fx
void union(int x,int y) //合并 x y 所在集合
{
int fx=find(x),fy=find(y); //找到两个节点对应的根节点
if(rank[fx]<rank[fy]) parent[fx]=fy; // fy 更高,将 fx 接在 fy 上
if(rank[fx]>rank[fy]) parent[fy]=fx; // fx 更高,将 fy 接在 fx 上
if(rank[fx]==rank[fy]) //二者等高,选择其一即可
{
parent[fx]=fy;
rank[fy]++;
}