本期梗概
本期我们将学习图论的基础
一、图的基本概念
(1)无向图:每条边都是无方向的;
(2)有向图:每条边都是有方向的;
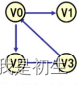
(3)完全图 :任意两个顶点上都存在一个边;
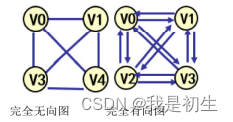
a、n个顶点的完全无向图有条边。
b、n个顶点的完全有向图有条边。
c、无向图G中顶点数为n,则图G至少有条边,至多有
条边;若G为有向图,则至少有
条边,至多有
条边。
(4)子图:从图中取出的部分集合;
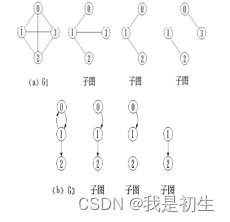
(5)带权图:边上带权的图;(权:具有某种含义的数值,如表示两点间的距离)
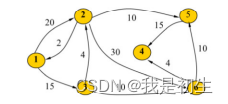
(6)连通图 :无向图任意两点都存在路径可达;
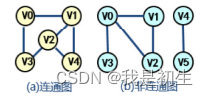
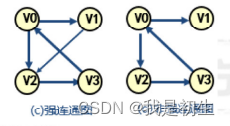
(7)强连通图:有向图中,若任意两个顶点都存在路径可达;
(8)顶点的度:与顶点有关的边的数目;
有向图又分为出度和入度;
顶点V的出度=以V为起点有向边数;
顶点V的入度=以V为终点有向边数
顶点V的度=V的出度+V的入度;
图的度=图中所有顶点度的和;
问题:一个图的顶点数为n,边数为e,则该图的度=。
(9)路径与回路:
路径:顶点A到顶点B的经过的所有边;
简单路径:在一条路径中除起点和终点外,若其余顶点各个不相同;
回路:起点和终点相同的路径;
简单回路:由简单路径组成的回路称为简单回路;
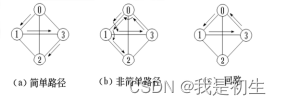
(10)连同分量:在无向图中,如果从顶点vi到vj连通。如果图中任意两个顶点之间都连通,则称该图为连通图,否则,将其中较大的连通子图称为连同分量。
在有向图中,如果对于每一对顶点vi和vj,从vi到vj和从vj到vi都有路径,则称该图为强连通图;否则,将其中的极大连通子图称为强连通分量。
二、图的储存
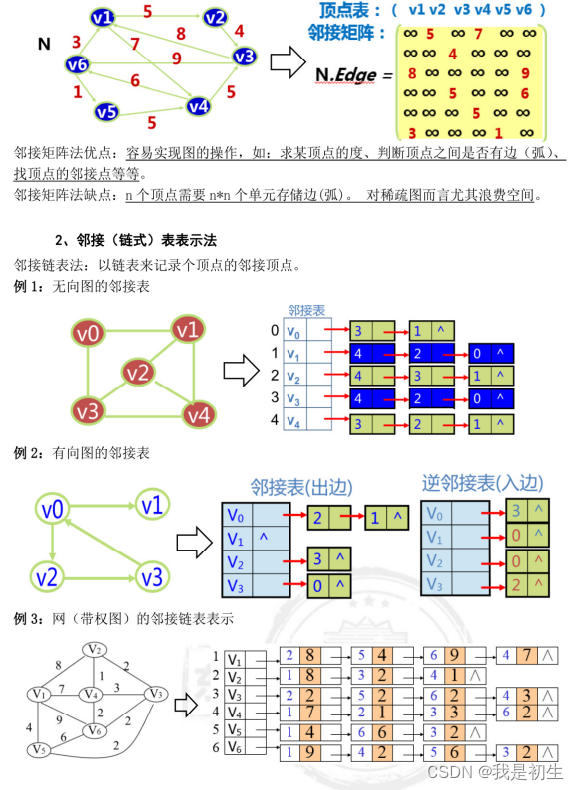
1、邻接矩阵(数组)表示法
邻接数组表示法是以一个n*n的数组来表示一个具有n个顶点的图形。我们以数组的索引(下标)值来表示顶点,以数组的内容之来表示边是否存在。