❤机器学习正则化算法的总结。耗时10个小时完成。❤

yaoyao在發光2024-06-06 18:54

❤纯 干 货~❤

目录

纯干货

[1、L1 正则化（Lasso 正则化）](#1、L1 正则化（Lasso 正则化）)

[2、L2 正则化（岭正则化）](#2、L2 正则化（岭正则化）)

[3、弹性网络正则化（Elastic Net 正则化）](#3、弹性网络正则化（Elastic Net 正则化）)

[4、Dropout 正则化（用于神经网络）](#4、Dropout 正则化（用于神经网络）)

5、贝叶斯Ridge和Lasso回归

贝叶斯Ridge回归

贝叶斯Lasso回归

6、早停法（Ear

7、数据增强

正则化是一种用于降低机器学习模型过拟合风险的技术。当模型过度拟合训练数据时，它会在新样本上表现不佳。所以为了解决这个问题，我们必须要引入正则化算法。

正则化通过在模型的损失函数中添加一个正则项（惩罚项）来实现。这个正则项通常基于模型参数的大小，以限制模型参数的数量或幅度。主要有两种常见的正则化算法：L1正则化和L2正则化。

  • L1正则化（Lasso）：L1正则化添加了模型参数的绝对值之和作为正则项。它倾向于使一些参数变为零，从而达到特征选择的效果。所以，L1正则化可以用于自动选择最重要的特征，并减少模型复杂度。

  • L2正则化（Ridge）：L2正则化添加了模型参数的平方和作为正则项。它倾向于使所有参数都较小，但没有明确地将某些参数设置为零。L2正则化对异常值更加鲁棒，并且可以减少模型的过度依赖单个特征的情况。

正则化通过控制模型参数的大小来限制模型的复杂度，从而避免过拟合。在损失函数中引入正则项后，模型的优化目标变为最小化损失函数和正则项之和。

今天要探究的是这7各部分，大家请看~

  • L1 正则化

  • L2 正则化

  • 弹性网络正则化

  • Dropout 正则化

  • 贝叶斯Ridge和Lasso回归

  • 早停法

  • 数据增强

1、L1 正则化（Lasso 正则化）

L1正则化（也称为Lasso正则化）是一种用于控制机器学习模型复杂度的技术。

通过向损失函数添加L1范数项来实现正则化，鼓励模型产生稀疏权重，即将一些特征的权重调整为0。

公式：

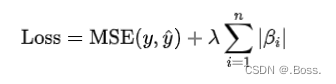
L1正则化在优化过程中有两个关键特点：

1、由于正则化项中包含绝对值操作，导致损失函数不可导。因此，在求解最小化损失函数时，需要使用其他方法（如坐标下降、梯度下降等）。

2、正则化项的存在促使部分特征的权重变为0，从而实现特征选择和模型简化。

咱们看一个简单案例，使用了sklearn库中的Lasso类来实现L1正则化的模型：

python 复制代码 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso

# 生成示例数据
np.random.seed(42)
X = np.linspace(-5, 5, num=100).reshape(-1, 1)
y = 2 * X + np.random.normal(0, 1, size=(100, 1))

# 创建Lasso模型对象
lasso = Lasso(alpha=0.1)  # 设置alpha参数，控制正则化强度

# 拟合数据
lasso.fit(X, y)

# 绘制优化复杂图形
fig, ax = plt.subplots()
ax.scatter(X, y, color="blue", label="Data")
ax.plot(X, lasso.predict(X), color="red", linewidth=2, label="L1 Regularization")

# 在图中绘制L1正则化项的等高线
beta_0 = np.linspace(-10, 10, 100)
beta_1 = np.linspace(-10, 10, 100)
B0, B1 = np.meshgrid(beta_0, beta_1)
Z = np.zeros_like(B0)
for i in range(len(beta_0)):
    for j in range(len(beta_1)):
        lasso.coef_ = np.array([B0[i,j], B1[i,j]])
        Z[i,j] = np.sum(np.abs(lasso.coef_))
ax.contour(B0, B1, Z, levels=20, colors="black", alpha=0.5)

ax.set_xlabel("X")
ax.set_ylabel("y")
ax.set_title("L1 Regularization with Contour Plot")
ax.legend()
plt.show()

除了绘制原始数据点和经过L1正则化的拟合线外，我们还使用等高线图形展示了L1正则化项。通过等高线图，可以更加直观地看到正则化项对权重的影响，以及如何促使模型产生稀疏权重。

2、L2 正则化（岭正则化）

L2正则化（也称为岭正则化）是一种用于控制机器学习模型复杂度的技术。

它通过向损失函数添加L2范数项来实现正则化，鼓励模型产生平滑权重，即将特征的权重调整为较小的值。

公式：

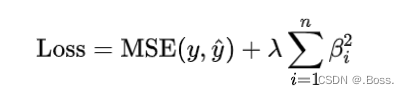
L2正则化在优化过程中的2个关键特点：

1、正则化项中包含平方操作，使得损失函数可导。因此，在求解最小化损失函数时，可以使用常见的梯度下降等优化算法。

2、正则化项的存在使得特征权重趋向于较小的值，从而避免了过拟合问题。

先看一个案例，使用sklearn库中的Ridge类来实现L2正则化的模型：

python 复制代码 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge

# 生成示例数据
np.random.seed(42)
X = np.linspace(-5, 5, num=100).reshape(-1, 1)
y = 2 * X + np.random.normal(0, 1, size=(100, 1))

# 创建Ridge模型对象
ridge = Ridge(alpha=0.1)  # 设置alpha参数，控制正则化强度

# 拟合数据
ridge.fit(X, y)

# 绘制优化复杂图形
fig, ax = plt.subplots()
ax.scatter(X, y, color="blue", label="Data")
ax.plot(X, ridge.predict(X), color="red", linewidth=2, label="L2 Regularization")

# 在图中绘制L2正则化项的等高线
beta_0 = np.linspace(-10, 10, 100)
beta_1 = np.linspace(-10, 10, 100)
B0, B1 = np.meshgrid(beta_0, beta_1)
Z = np.zeros_like(B0)
for i in range(len(beta_0)):
    for j in range(len(beta_1)):
        ridge.coef_ = np.array([B0[i,j], B1[i,j]])
        Z[i,j] = np.sum(ridge.coef_ ** 2)
ax.contour(B0, B1, Z, levels=20, colors="black", alpha=0.5)

ax.set_xlabel("X")
ax.set_ylabel("y")
ax.set_title("L2 Regularization with Contour Plot")
ax.legend()
plt.show()

除了绘制原始数据点和经过L2正则化的拟合线外，我们还使用等高线图形展示了L2正则化项。通过等高线图，可以更加直观地看到正则化项对权重的影响，以及如何促使模型产生平滑权重。

3、弹性网络正则化（Elastic Net 正则化）

弹性网络正则化是一种用于线性回归模型的正则化方法，结合了L1和L2正则化的特点。

可以在具有大量特征的数据集上处理多重共线性问题，并选择相关特征。

弹性网络正则化通过加权L1范数和L2范数来控制正则化项的大小。L1范数在某些情况下会产生稀疏解（即部分系数为零），而L2范数鼓励系数的平滑性。

因此，弹性网络正则化可以综合利用L1和L2正则化的优势。

弹性网络正则化的损失函数可以表示为：

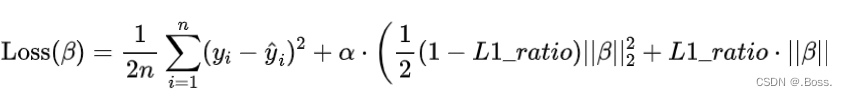
下面是使用Python的scikit-learn库来拟合弹性网络回归模型：

python 复制代码 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ElasticNet

# 生成一些样本数据
np.random.seed(42)
n_samples = 100
X = np.linspace(-3, 3, n_samples)
y = 0.5 * X + np.random.normal(scale=0.5, size=n_samples)

# 创建并拟合弹性网络模型
enet = ElasticNet(alpha=0.5, l1_ratio=0.7)
enet.fit(X.reshape(-1, 1), y)

# 绘制原始数据和拟合曲线
plt.scatter(X, y, color='b', label='Original data')
plt.plot(X, enet.predict(X.reshape(-1, 1)), color='r', linewidth=2, label='Elastic Net')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title('Elastic Net Regression')
plt.show()

代码中生成了一些具有噪声的样本数据，并使用弹性网络模型进行拟合。

通过绘制原始数据和拟合曲线，可以更好地理解弹性网络正则化在回归问题中的应用。

案例中只是一个简单的示例，实际使用时需要调整参数和改进模型以适应具体问题。

4、Dropout 正则化（用于神经网络）

Dropout 正则化是一种用于神经网络的正则化方法。

通过在训练过程中随机将一部分神经元的输出设置为零，从而减少神经网络中的过拟合现象。

Dropout 正则化可以提高模型的泛化能力，并防止神经元之间过度依赖。

Dropout 正则化的原理是，在训练期间以概率 随机地将一部分神经元的输出设置为零，称为"丢弃"。丢弃的方式是对每个神经元引入一个二进制的随机变量 ，取值为 0 或 1，表示该神经元是否被丢弃。在前向传播和反向传播过程中，丢弃的神经元及其连接会被忽略。

在训练过程中，Dropout 正则化的损失函数可以表示为：

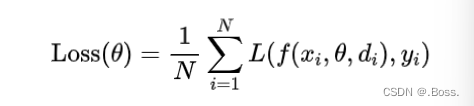
在测试阶段，不再进行丢弃操作，而是将所有神经元的输出乘以概率 P。通过这种方式，Dropout 正则化可以减少神经元之间的依赖性，提高模型的鲁棒性。

下面使用Python的tensorflow库来构建一个具有Dropout正则化的简单神经网络：

python 复制代码 
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf

# 生成一些样本数据
np.random.seed(42)
n_samples = 100
X = np.linspace(-3, 3, n_samples)
y = 0.5 * X + np.random.normal(scale=0.5, size=n_samples)

# 构建神经网络模型
model = tf.keras.models.Sequential([
    tf.keras.layers.Dense(16, activation='relu', input_shape=(1,)),
    tf.keras.layers.Dropout(0.5),
    tf.keras.layers.Dense(1)
])

# 编译和拟合模型
model.compile(optimizer='adam', loss='mean_squared_error')
model.fit(X, y, epochs=50, batch_size=16, verbose=0)

# 绘制原始数据和拟合曲线
plt.scatter(X, y, color='b', label='Original data')
plt.plot(X, model.predict(X), color='r', linewidth=2, label='Dropout Regularization')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title('Neural Network with Dropout Regularization')
plt.show()

上述代码生成了一些具有噪声的样本数据，并构建了一个简单的具有Dropout正则化的神经网络模型。通过绘制原始数据和拟合曲线，可以更好地理解Dropout正则化在神经网络中的应用。

5、贝叶斯Ridge和Lasso回归

贝叶斯Ridge回归和Lasso回归是两种基于贝叶斯统计思想的回归算法模型。它们都是经典的线性回归的扩展，可以用于特征选择和解决过拟合问题。

贝叶斯Ridge回归

贝叶斯Ridge回归通过引入正则化项来控制模型的复杂度，同时利用贝叶斯推断方法进行参数估计。其优化目标是最小化损失函数和正则化项的和。

贝叶斯Ridge回归的目标函数如下所示：

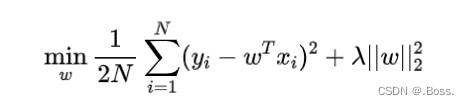
贝叶斯Ridge回归的核心思想是将权重参数视为一个随机变量，并使用贝叶斯推断对其进行估计。

通过引入先验分布p(W)，根据贝叶斯定理可以得到后验分布P(W|X,y)。然后，可以通过采样或其他方法来估计权重参数的分布，从而得到预测结果。

贝叶斯Ridge回归的优点是可以灵活地处理不同类型的数据和噪声，并且可以用作特征选择方法。缺点是计算复杂度较高，需要进行概率推断。

贝叶斯Lasso回归

贝叶斯Lasso回归也是一种基于贝叶斯统计思想的回归模型。它与贝叶斯Ridge回归类似，但使用的是L1范数正则化项。

贝叶斯Lasso回归的目标函数如下所示：

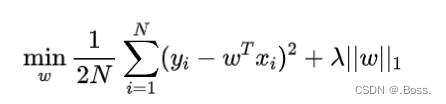
贝叶斯Lasso回归通过最小化损失函数和L1范数正则化项来实现稀疏性。L1范数倾向于将一些权重参数设为0，从而实现特征选择。

贝叶斯Lasso回归的优点是可以自动进行特征选择，并且能够处理高维数据。缺点是计算复杂度较高，需要进行概率推断。

以贝叶斯Ridge回归为例，使用Python代码实现：

python 复制代码 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import BayesianRidge

# 生成示例数据集
np.random.seed(42)
X = np.random.rand(100, 1) * 10
y = 2 * X[:, 0] + np.random.randn(100)

# 创建贝叶斯Ridge回归模型对象
model = BayesianRidge()

# 拟合模型
model.fit(X, y)

# 绘制原始数据和拟合曲线
fig, ax = plt.subplots()
ax.scatter(X, y, color='blue', label='Original data')

# 生成用于预测的新样本点
x_new = np.linspace(0, 10, 100).reshape(-1, 1)

# 预测新样本点的输出值
y_pred, y_std = model.predict(x_new, return_std=True)

# 绘制拟合曲线及置信区间
ax.plot(x_new, y_pred, color='red', label='Fitted curve')
ax.fill_between(x_new.flatten(), y_pred - y_std, y_pred + y_std, color='pink',
                alpha=0.5, label='Confidence interval')

ax.set_xlabel('X')
ax.set_ylabel('y')
ax.set_title('Bayesian Ridge Regression')
ax.legend()
plt.show()

6、早停法（Ear

早停法（Early Stopping）是一种用于防止模型过拟合的正则化技术。它通过在训练过程中监测验证误差，并根据验证误差的变化来确定何时停止训练模型，以避免过拟合。

早停法采用以下步骤：

  1. 将数据集划分为训练集和验证集。

  2. 初始化模型参数。

  3. 在每个训练迭代中，计算训练误差并更新模型参数。

  4. 在每个训练迭代后，计算验证误差。

  5. 如果验证误差开始上升，则停止训练，并使用具有最低验证误差的模型参数作为最终模型。

公式：

早停法的目标是在验证误差开始上升之前找到最佳模型，即训练误差和验证误差同时达到较小值的点。

下面是一个Python实现的案例：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

# 生成示例数据
np.random.seed(42)
X = np.linspace(-5, 5, num=100).reshape(-1, 1)
y = 2 * X + np.random.normal(0, 1, size=(100, 1))

# 划分训练集和验证集
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建线性回归模型对象
model = LinearRegression()

# 记录训练误差和验证误差
train_errors = []
val_errors = []

# 拟合数据并记录误差
for i in range(1, len(X_train)):
    model.fit(X_train[:i], y_train[:i])
    y_train_pred = model.predict(X_train[:i])
    y_val_pred = model.predict(X_val)
    train_errors.append(np.mean((y_train_pred - y_train[:i]) ** 2))
    val_errors.append(np.mean((y_val_pred - y_val) ** 2))
    
# 绘制优化复杂图形
fig, ax = plt.subplots()
ax.plot(train_errors, label="Train Error")
ax.plot(val_errors, label="Validation Error")

best_epoch = np.argmin(val_errors)
ax.axvline(x=best_epoch, linestyle="--", color="red", label="Early Stopping")

ax.set_xlabel("Epoch")
ax.set_ylabel("Mean Squared Error")
ax.set_title("Early Stopping")
ax.legend()
plt.show()

代码证，使用了线性回归模型，并在每个训练迭代中记录了训练误差和验证误差。通过绘制训练误差和验证误差的曲线，以及早停法的标记点，可以更加直观地观察到模型的优化过程和选择最佳模型时的判定点。

这样，使用优化复杂的图形可以更好地理解早停法算法模型的效果。

7、数据增强

数据增强正则化是一种常用的正则化技术，它通过对训练数据进行随机变换或扩充来增加数据集的多样性。这种方法可以帮助模型更好地泛化，并减轻过拟合问题。

数据增强正则化的步骤如下：

1、对训练数据进行一系列随机的变换操作，例如旋转、平移、缩放、裁剪等。

2、将变换后的样本添加到原始训练数据集中。

3、使用经过增强的数据集进行模型训练。

数据增强正则化的目标是通过增加数据集的多样性，使模型能够更好地适应不同的输入情况，并提高其泛化能力。

由于数据增强正则化是一种基于随机变换的方法，没有明确的公式表达。

代码示例：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.linear_model import LogisticRegression

# 生成示例数据集
np.random.seed(42)
X, y = make_moons(n_samples=200, noise=0.1)

# 创建Logistic回归模型对象
model = LogisticRegression()

# 绘制原始数据分布
fig, ax = plt.subplots()
ax.scatter(X[:, 0], X[:, 1], c=y, cmap="bwr", edgecolors='k')
ax.set_xlabel("X1")
ax.set_ylabel("X2")
ax.set_title("Original Data Distribution")

# 数据增强
n_transforms = 50
augmented_X = []
augmented_y = []
for i in range(n_transforms):
    transformed_X = X + np.random.normal(0, 0.05, size=X.shape)
    augmented_X.append(transformed_X)
    augmented_y.append(y)
    
augmented_X = np.concatenate(augmented_X, axis=0)
augmented_y = np.concatenate(augmented_y, axis=0)

# 绘制经过数据增强后的数据分布
fig, ax = plt.subplots()
ax.scatter(augmented_X[:, 0], augmented_X[:, 1], c=augmented_y, cmap="bwr", edgecolors='k')
ax.set_xlabel("X1")
ax.set_ylabel("X2")
ax.set_title("Data Distribution after Augmentation")

# 使用经过增强的数据进行模型训练
model.fit(augmented_X, augmented_y)

# 绘制决策边界
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                     np.arange(y_min, y_max, 0.02))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

fig, ax = plt.subplots()
ax.contourf(xx, yy, Z, alpha=0.8, cmap="bwr")
ax.scatter(X[:, 0], X[:, 1], c=y, cmap="bwr", edgecolors='k')
ax.set_xlabel("X1")
ax.set_ylabel("X2")
ax.set_title("Decision Boundary")

plt.show()

在代码示例中，我们使用了make_moons函数生成了一个月亮形状的二分类数据集。然后，通过对原始数据进行随机的高斯扰动（np.random.normal），生成了多个变换后的样本，并将这些样本添加到原始数据集中。最后，使用经过增强的数据集训练了Logistic回归模型，并绘制了决策边界。

通过增强后的数据集，模型能够更好地捕捉到数据的不同特征和变化，使得模型能够更好地区分两个类别。而绘制的决策边界显示了模型在增强后的数据上学到的决策规则。

这种可视化方法有助于理解数据增强正则化的作用，以及如何通过引入多样性来改善模型的泛化能力。

实际应用中可能需要根据具体情况进行调整或使用其他数据增强技术。同时，数据增强正则化算法模型有许多变体和技巧，可以根据具体任务和需求进行调整和改进。

相关推荐
吃个糖糖3 分钟前
35 Opencv 亚像素角点检测
人工智能·opencv·计算机视觉
努力学习编程的伍大侠6 分钟前
基础排序算法
数据结构·c++·算法
qq_5290252920 分钟前
Torch.gather
python·深度学习·机器学习
数据小爬虫@21 分钟前
如何高效利用Python爬虫按关键字搜索苏宁商品
开发语言·爬虫·python
XiaoLeisj34 分钟前
【递归，搜索与回溯算法 & 综合练习】深入理解暴搜决策树：递归，搜索与回溯算法综合小专题（二）
数据结构·算法·leetcode·决策树·深度优先·剪枝
Cachel wood1 小时前
python round四舍五入和decimal库精确四舍五入
java·linux·前端·数据库·vue.js·python·前端框架
IT古董1 小时前
【漫话机器学习系列】017.大O算法（Big-O Notation）
人工智能·机器学习
Jasmine_llq1 小时前
《 火星人 》
算法·青少年编程·c#
凯哥是个大帅比1 小时前
人工智能ACA（五）--深度学习基础
人工智能·深度学习
热门推荐
01〔AI 绘画〕Stable Diffusion 之 解决绘制多人或面部很小的人物时面部崩坏问题 篇02ARM学习（31）编译器对overlay方式的支持03玄机平台应急响应—webshell查杀04DisplayPort AltMode On Type-c协议_Ver2.0(学习笔记)05校验 GPT-4 真实性的三个经典问题：快速区分 GPT-3.5 与 GPT-4，并提供免费测试网站06Docker 夺命连环 15 问076个主流的工业3D管道设计软件08基于大语言模型（LLM）的合成数据生成、策展和评估的综述09(欧拉)openEuler系统添加网卡文件配置流程、(欧拉)openEuler系统手动配置ipv6地址流程、(欧拉)openEuler系统网络管理说明10红米手机使用google play