【数据结构】图论入门

引入

数据的逻辑结构：

集合：数据元素间除"同属于一个集合"外，无其他关系
线性结构：一个对多个，例如：线性表、栈、队列
树形结构：一个对多个，例如：树
图形结构：多个对多个，例如：图

图的基本概念及术语

图：G = ( V, E )

V：顶点（数据元素）的有穷非空集合

E：边的有穷集合

图的类型定义

无向图：每条边都是无方向的

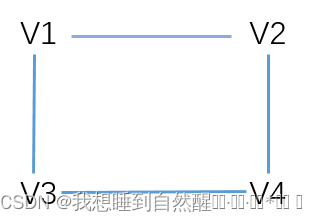
有向图：每条弧都是有方向的

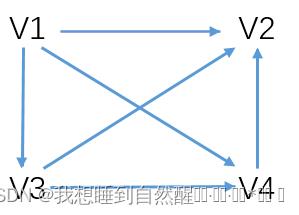
完全图：任意两个点都有一条边相连

无向完全图：n个结点就有n * (n - 1) / 2 条边
有向完全图：n个结点就有n * (n - 1) 条边

稀疏图：有很少的边或者弧的图（通常 m 远小于nlog(n)）

稠密图：有较多的边或者弧的图（通常 m 大于nlog(n)）

连通图：在无（有）向图G = (V,{E})中，若对任意两个顶点v、u，都存在v到u的路径，则称G是连通图（强连通图）

图的基本术语

网：边或者弧带权（有值）的图
邻接：有边 / 弧相连的两个顶点之间的关系
- 存在（Vi，Vj），则称 Vi 和 Vj 互为邻接点（无向图）
- 存在 <Vi，Vj>，则称 Vi 邻接到Vj，Vj 邻接于 Vi（有向图）
关联（依附）：边 / 弧与顶点之间的关系

存在（Vi，Vj）/ <Vi，Vj>，则称该边/弧关联与Vi和Vj
顶点的度：与该顶点相关联的边的数目，记为TD(V)

在有向图当中，顶点的度等于该顶点的入度与出度之和

顶点V的入度是以V为终点的有向边的条数

以上图为例：

对于上面的有向图来说，每个结点的度都为2

对于上面的无向图来说，每个结点的度都为3，但是不同结点的入度、出度不一样（V3入度为1，出度为2）
路径：连接的边构成的顶点序列
路径长度：路径上边/弧的数目/权值之和
回路（环）：第一个顶点和最后一个顶点相同的路径
简单路径：除路径起点和终点可以相同之外，其余顶点均不相同的路径
简单回路（简单环）：除路径起点和终点相同之外，其余顶点均不相同的路径
子图：设有两个图G = (V,{E})，G1 = (V1,{E1})，若V1属于V并且E1属于E，则称G1是G的子图
连通分量（强连通分量）：无（有）向图的极大连通子图称为G的连通分量（强连通分量）
- 极大连通子图：该子图是G连通子图，将G的任何不在该子图的顶点加入，此图不再连续
- 极小连通子图：该子图是G的连通子图，在该子图中删除任何一条边，此子图不再连续

图的存储结构

数组（邻接矩阵）表示法

概述

建立一个顶点表（记录各个顶点信息）和一个邻接矩阵（表示各个顶点之间的关系）

设图A = (V,E)有n个顶点，则顶点表Vext[n]表示为

i 0 1 ... n-1

Vext[i] V1 V2 ... Vn
图的邻接矩阵是一个二维数组A.arcs[n][n],定义为：

当存在<i,j>或者( i,j )属于图中的边或者弧，我们就将A.arcs[i][j]赋值为1，否则为0

i	0	1	...	n-1
Vext[i]	V1	V2	...	Vn

举例

无向图

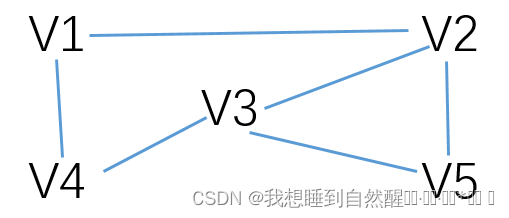
具体形况根据顶点的值去建立顶点表

邻接矩阵：

	V1	V2	V3	V4	V5
V1	0	1	0	1	0
V2	1	0	1	0	1
V3	0	1	0	1	1
V4	1	0	1	0	0
V5	0	1	1	0	0

特点：

无向图的邻接矩阵是对称的
顶点i的度 = 第i行（列）中1的个数
完全图的邻接矩阵中，对角元素为0，其余为1

代码演示见下面遍历部分

有向图

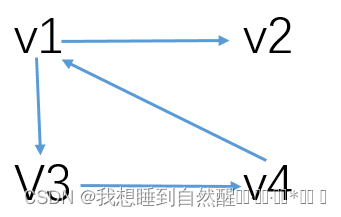
邻接矩阵：

	v1	v2	v3	v4
v1	0	1	1	0
v2	0	0	0	0
v3	0	0	0	1
v4	1	0	0	0

特点：

有向图的邻接矩阵可能是不对称的
顶点的出度 = 第i行元素之和

顶点的入度 = 第i列元素之和

顶点的度 = 出度 + 入度

网的邻接矩阵就是将1用权值替换

代码演示见下面遍历部分

优缺点

优点：

直观，简单，好理解
方便检查任意一对顶点间是否存在边
方便找任意顶点的所有邻接点
方便计算出任意顶点的度

缺点：

不利于增加和删除顶点
浪费空间：存稀疏图，有大量无效元素
浪费时间：统计稀疏图中共有多少条边

邻接表

顶点：按编号顺序将顶点数据存储在一维数组中

关联同一顶点的边（以顶点为尾的弧）：用线性链表存储

举例

仍以上图为例

无向图：

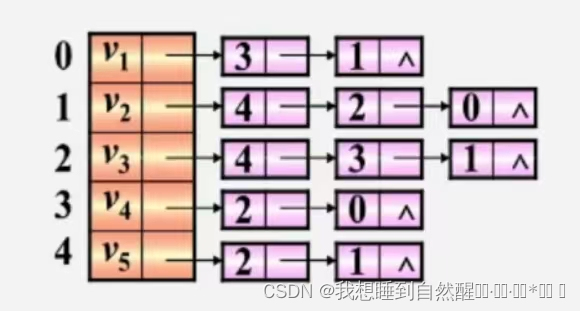
特点：

邻接表不唯一
若无向图中有n个顶点e条边，则其邻接表需n个头结点和2e个表结点，适宜存储稀疏图
无向图中顶点vi的度为第i个单链表中的结点数

代码演示见下面遍历部分

有向图：

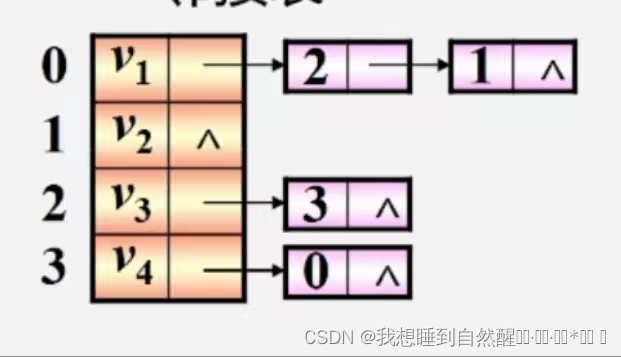
特点：

顶点vi的出度为第i个单链表中的结点个数
顶点vi的入度为整个单链表中邻接点域值是i-1的结点个数

代码演示见下面遍历部分

邻接矩阵与邻接表的关系:

1.联系：邻接表中每个链表对应于邻接矩阵中的每一行，链表中结点个数等于一行中非零元素的个数

2.区别：

a.对于任意确定的无向图，邻接矩阵是唯一的(行列号与顶点编号一致)，但邻接表不唯一（连接次序与顶点编号无关）

b.邻接矩阵的空间复杂度为O(n^2)，而连接表的空间复杂度为O(n+e)

图的遍历

定义：从已给的连通图中某一顶点出发，沿着一些边访问图中所有的顶点，且每个顶点仅被访问一次，就叫做图的遍历，它是图的基本运算

实质：找每个顶点的邻接点的过程

问题：由图的特点，图中可能出现回路，且图的任一顶点都可能与其他结点相遇，在访问完某个顶点之后可能会沿着某些边又回到了曾经访问过的顶点，怎么避免重复访问？

解决思路：设置辅助数组a[n]，用来标记每个被访问过的顶点，初始状态都为0，当顶点i被访问，改a[i]为1，防止被多次访问

深度优先搜索（DFS）

方法：

在访问图中某一起始顶点v后，由v出发，访问它的任一邻接顶点w1
再由w1出发访问与w1邻接，但还未被访问过的顶点w2
然后再从w2出发进行类似的访问...
如此进行下去，直至到达所有的邻接顶点都被访问过的顶点u为止
接着退回一步退到前一次刚访问过的顶点，看是否还有其他没有被访问的邻接顶点
如果有则访问此顶点，之后再从此顶点出发，进行与之前类似的访问
如果没有就再退回一步进行搜索，重复上述过程，直到连通图中所有顶点都被访问过为止

注意：

稠密图适于在邻接矩阵上进行深度遍历
稀疏图适于在连接表上进行深度遍历

对于邻接矩阵的代码演示：

java 复制代码

public class GraphAdjacencyMatrix {
    private int V; // 顶点的数量
    private int[][] matrix; // 邻接矩阵
    private boolean[] visited;
    // 构造函数
    public GraphAdjacencyMatrix(int v) {
        V = v;
        matrix = new int[v][v];
        visited = new boolean[v];
        for (int i = 0; i < v; i++) {
            visited[i] = false;
        }
    }

    // 添加边
    public void addEdge(int v, int w, int weight) {
        matrix[v][w] = weight; // 因为是无向图，所以需要添加两个方向的边
        matrix[w][v] = weight;
    }

    //深度优先遍历
    private void DFS(int v) {
        visited[v] = true;
        System.out.print(v + " ");

        for (int i = 0; i < V; i++) {
            if (matrix[v][i] == 1 && !visited[i]) {
                DFS(i);
            }
        }
    }

    // 遍历所有顶点（如果顶点未访问，则进行DFS）
    public void DFSTraversal() {
        for (int i = 0; i < V; i++) {
            if (!visited[i]) {
                DFS(i); // 从顶点i开始DFS
            }
        }
    }

    // 打印图
    public void printGraph() {
        for (int i = 0; i < V; i++) {
            for (int j = 0; j < V; j++) {
                if (matrix[i][j] == 0) {
                    System.out.print("0 ");
                } else {
                    System.out.print(matrix[i][j] + " ");
                }
            }
            System.out.println();
        }
    }
}

java 复制代码

public class linjiejuzhen {
    public static void main(String[] args) {
        GraphAdjacencyMatrix graph = new GraphAdjacencyMatrix(4);

        graph.addEdge(0, 1, 10); // 添加边 0-1 权重为 10
        graph.addEdge(0, 2, 6);
        graph.addEdge(1, 2, 4);
        graph.addEdge(2, 3, 1);

        System.out.println("Adjacency Matrix:");
        graph.printGraph();
        System.out.println("Depth First Traversal starting from vertex 0: ");
        graph.DFSTraversal(); //0 1 2 3
    }
}

Adjacency Matrix:
0 10 6 0 
10 0 4 0 
6 4 0 1 
0 0 1 0 
Depth First Traversal starting from vertex 0: 
0 1 2 3

对于邻接表代码演示：

java 复制代码

import java.util.Iterator;
import java.util.LinkedList;

public class DirectedGraphAdjacencyList {
    private int V; // 顶点的数量
    private LinkedList<Integer> adj[];
    private boolean visited[]; // 邻接表

    // 构造函数
    public DirectedGraphAdjacencyList(int v) {
        V = v;
        adj = new LinkedList[v];
        visited = new boolean[v];
        for (int i = 0; i < v; i++) {
            adj[i] = new LinkedList<>();
            visited[i] = false;
        }
    }

    // 添加边
    public void addEdge(int v, int w) {
        adj[v].add(w); // 添加从顶点v到顶点w的有向边
    }

    // 打印图
    public void printGraph() {
        for (int i = 0; i < V; i++) {
            System.out.print("Vertex " + i + ":");
            Iterator<Integer> it = adj[i].iterator();
            while (it.hasNext()) {
                System.out.print(" -> " + it.next());
            }
            System.out.println();
        }
    }

    private void DFS(int v) {
        visited[v] = true;
        System.out.print(v + " ");

        Iterator<Integer> i = adj[v].listIterator();
        while (i.hasNext()) {
            int n = i.next();
            if (!visited[n]) {
                DFS(n); // 递归访问未访问的邻接顶点
            }
        }
    }

    // 遍历所有顶点执行DFS
    public void DFSTraversal() {
        for (int i = 0; i < V; i++) {
            if (!visited[i]) {
                DFS(i); // 从顶点i开始DFS
            }
        }
    }
}

java 复制代码

public class DirectedGraphAdjacency {
    public static void main(String[] args) {
        DirectedGraphAdjacencyList graph = new DirectedGraphAdjacencyList(6);

        // 添加有向边
        graph.addEdge(5, 0);
        graph.addEdge(5, 3);
        graph.addEdge(4, 0);
        graph.addEdge(4, 1);
        graph.addEdge(2, 3);
        graph.addEdge(3, 1);
        graph.addEdge(1, 3);

        System.out.println("Adjacency List Representation of Directed Graph:");
        graph.printGraph();
        System.out.println("Depth First Traversal starting from vertex 0: ");
        graph.DFSTraversal(); //0 1 3 2 4 5
    }
}

Adjacency List Representation of Directed Graph:
Vertex 0:
Vertex 1: -> 3
Vertex 2: -> 3
Vertex 3: -> 1
Vertex 4: -> 0 -> 1
Vertex 5: -> 0 -> 3
Depth First Traversal starting from vertex 0: 
0 1 3 2 4 5

广度优先搜索（BFS）

方法：

从图的某一结点出发，首先依次访问该结点的所有邻接结点 Vi1、Vi2......Vin，再按这些顶点被访问的先后次序依次访问与他们相邻接的所有未被访问的顶点。重复此过程，直至所有顶点均被访问为止

对于邻接矩阵的代码演示

java 复制代码

import java.util.LinkedList;
import java.util.Queue;

public class DirectedGraphAdjacencyMatrix {
    private int V; // 顶点的数量
    private int[][] matrix; // 邻接矩阵
    private boolean[] visited;

    // 构造函数
    public DirectedGraphAdjacencyMatrix(int v) {
        V = v;
        matrix = new int[v][v];
        visited = new boolean[v];
        // 初始化矩阵，所有元素都设置为0，表示没有边
        for (int i = 0; i < v; i++) {
            for (int j = 0; j < v; j++) {
                matrix[i][j] = 0;
            }
            visited[i] = false;
        }
    }

    // 添加边
    public void addEdge(int v, int w, int weight) {
        matrix[v][w] = weight; // 只在矩阵的对应位置添加边的权重
    }

    // 打印图
    public void printGraph() {
        for (int i = 0; i < V; i++) {
            for (int j = 0; j < V; j++) {
                if (matrix[i][j] == 0) {
                    System.out.print(" 0 ");
                } else {
                    System.out.print(" " + matrix[i][j] + " ");
                }
            }
            System.out.println();
        }
    }
    //广度优先搜索
    public void BFS(int start) {
        Queue<Integer> queue = new LinkedList<>();
        visited[start] = true; // 标记起始顶点为已访问
        queue.add(start); // 将起始顶点添加到队列中

        while (!queue.isEmpty()) {
            int v = queue.poll(); // 从队列中取出一个顶点
            System.out.print(v + " ");

            for (int i = 0; i < V; i++) {
                if (matrix[v][i] != 0 && !visited[i]) {
                    visited[i] = true; // 标记邻接顶点为已访问
                    queue.add(i); // 将邻接顶点添加到队列中
                }
            }
        }
    }
}

java 复制代码

public class linjiejuzhenYou {
    public static void main(String[] args) {
        DirectedGraphAdjacencyMatrix graph = new DirectedGraphAdjacencyMatrix(4);

        graph.addEdge(0, 1, 10); // 添加有向边 0->1 权重为 10
        graph.addEdge(0, 2, 6);
        graph.addEdge(1, 2, 4);
        graph.addEdge(1, 3, 1);
        graph.addEdge(2, 3, 7);

        System.out.println("Directed Adjacency Matrix:");
        graph.printGraph();
        System.out.println("Breadth First Traversal starting from vertex 0: ");
        graph.BFS(0); //0 1 2 3
    }
}

Directed Adjacency Matrix:
 0  10  6  0 
 0  0  4  1 
 0  0  0  7 
 0  0  0  0 
Breadth First Traversal starting from vertex 0: 
0 1 2 3

对于邻接表的代码演示

java 复制代码

import java.util.Iterator;
import java.util.LinkedList;
import java.util.Queue;

public class UndirectedGraphAdjacencyList {
    private int V; // 顶点的数量
    private LinkedList<Integer> adj[]; // 邻接表
    private boolean[] visited;

    // 构造函数
    public UndirectedGraphAdjacencyList(int v) {
        V = v;
        visited = new boolean[V];
        adj = new LinkedList[v];
        for (int i = 0; i < v; i++) {
            adj[i] = new LinkedList<>();
            visited[i] = false;
        }
    }

    // 添加边
    public void addEdge(int v, int w) {
        adj[v].add(w); // 添加从v到w的边
        adj[w].add(v); // 因为是无向图，所以需要添加从w到v的边
    }

    // 打印图
    public void printGraph() {
        for (int i = 0; i < V; i++) {
            System.out.print("Vertex " + i + ":");
            Iterator<Integer> it = adj[i].iterator();
            while (it.hasNext()) {
                System.out.print(" -> " + it.next());
            }
            System.out.println();
        }
    }

    public void BFS(int start) {
        Queue<Integer> queue = new LinkedList<>();
        visited[start] = true; // 标记起始顶点为已访问
        queue.add(start); // 将起始顶点添加到队列中

        while (!queue.isEmpty()) {
            int v = queue.poll(); // 从队列中取出一个顶点
            System.out.print(v + " ");

            Iterator<Integer> i = adj[v].listIterator();
            while (i.hasNext()) {
                int n = i.next();
                if (!visited[n]) {
                    visited[n] = true; // 标记邻接顶点为已访问
                    queue.add(n); // 将邻接顶点添加到队列中
                }
            }
        }
    }
}

java 复制代码

public class UndirectedGraphAdjacency {
    public static void main(String[] args) {
        UndirectedGraphAdjacencyList graph = new UndirectedGraphAdjacencyList(4);

        graph.addEdge(0, 1); // 添加边 0-1
        graph.addEdge(0, 2);
        graph.addEdge(1, 2);
        graph.addEdge(2, 3);

        System.out.println("Adjacency List Representation of Undirected Graph:");
        graph.printGraph();
        System.out.println("Breadth First Traversal starting from vertex 0: ");
        graph.BFS(0); //0 1 2 3
    }
}

Adjacency List Representation of Undirected Graph:
Vertex 0: -> 1 -> 2
Vertex 1: -> 0 -> 2
Vertex 2: -> 0 -> 1 -> 3
Vertex 3: -> 2
Breadth First Traversal starting from vertex 0: 
0 1 2 3

二者搜索的算法分析

时间复杂度：

邻接矩阵：

对于邻接矩阵表示的图，时间复杂度主要受两个因素影响：

矩阵大小：邻接矩阵的大小为 𝑉×𝑉，其中 V 是顶点的数量。
遍历矩阵：你需要遍历整个邻接矩阵来检查每个顶点的所有邻接点。

因此，对于邻接矩阵表示的图，时间复杂度为 𝑂(𝑉^2)，这是因为你需要检查 V 个顶点，每个顶点可能与其他 V 个顶点相连。

邻接表：

对于邻接表表示的图，时间复杂度分析如下：

顶点数量：图有 V 个顶点。
边的数量：图有 E 条边。
访问邻接表：你访问每个顶点的邻接表，每个邻接表包含与该顶点直接相连的顶点。
队列操作：使用队列（栈）来存储待访问的顶点，每次从队列（栈）中取出一个顶点，并将其所有未访问的邻接顶点加入队列（栈）。

因此，对于邻接表表示的图，时间复杂度为 O(V+E)。这是因为你访问了所有 V 个顶点，并且每个顶点的邻接表（即所有边）也被访问了一次。

空间复杂度：空间复杂度相同，都是O(n)