从本专栏开始,笔者正式研究演化博弈分析,其中涉及到双方演化博弈分析,三方演化博弈分析,复杂网络博弈分析等等。
先阅读了大量相关的博弈分析的文献,总结了现有的研究常用的研究流程,针对每个流程进行拆解。具体学习每个步骤中的步骤的实现方法和流程。基础性文章,希望对您有帮助,如果存在错误或不足之处,还请海涵。且看且珍惜!
文章目录
- [1. 期望计算](#1. 期望计算)
- [2. 复制动态方程构建](#2. 复制动态方程构建)
- [3. MATLAB计算期望与复制动态方程](#3. MATLAB计算期望与复制动态方程)
1. 期望计算
在计算期望收益之前,需要先计算出每个参与主体的收益,如下表1所示。
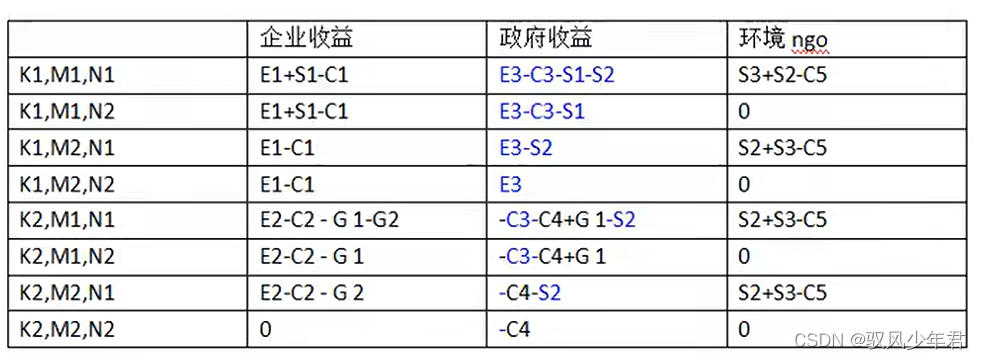
采取应对策略的概率:

首先,一般需要构建每个主体在采取,和不采取策略的期望收益,以及平均从期望收益,通常是构建三个期望收益等式。
企业的收益期望如下所示:

分别计算出采取和不采取的策略下的收益值与对应策略其他主体之间应对策略的概率之和:
计算出来的结果如下所示,具体的计算结果根据公式对应进去计算就可以

同理,可以根据以上的算式,算出其他主体的期望收益:


2. 复制动态方程构建
复制动态 和 演化稳定策略 是演化博弈理 论的两个核心范畴。"复制动态"是对有限理性的 参与主体策略调整过程的动态描述和分析
需要分别构造企业、政府和环境 NGO 行为策略的复制动态方程
其中复制动态方程=dx/dt=采取概率(采取期望收益 - 平均期望收益)
这个复制动态方程的构建,通常学者都是这么计算,只需要将上文的计算机过套入,并对式子进行化简处理。



通过以上的方程,就可以构建出每个主体之间的动态方程。
构建动态方程后,就可以进行博弈分析中最重要的均衡点分析。
3. MATLAB计算期望与复制动态方程
每个主体的期望,可以通过我们手动进行构建
构建出每个主体的期望后,我们需要计算出平均期望和复制动态方程。我们只需要将方程对应的等式带入就可以,但是在文章中需要展现的是经过你自己整理后,最简的方程式。
因此,需要有一个手动计算的过程,手动计算容易出错,因此可以借助MatLAB实现一个化简的功能。
主要借助的就是simplify函数。
如下所示
matlab
%定义相应的参数
syms x y z e1 e2 e3 c1 c2 c3 c4 c5 s1 s2 s3 g1 g2;
%计算出第一个主体的期望
v11=(e1-c1+s1)*y*z+(e1-c1-s1)*y*(1-z)+(e1-c1)*(1-y)*z+(e1-c1)*(1-y)*(1-z);
v12=(e2-c2-g1-g2)*y*z+(e2-c2-g1)*y*(1-z)+(e2-c2-g2)*(1-y)*z;
%化简平均期望
v1=simplify(x*v11+(1-x)*v12)
%化简复制动态方程
fx=simplify(x*(v11-v1))通过以上的原理,可以计算出每个主体的期望与复制动态方程的值
当用simplify函数实现化简后,如果未达到最简可以自己手动再进行一次化简。