我们之前介绍了二叉搜索树的相关知识。作为算法领域的重要数据结构,二叉搜索树也是面试中的高频考点。本文将重点讲解几个二叉搜索树的典型习题。
相关代码已经上传至作者的个人gitee:CPP 学习代码库: C++代码库新库,旧有C++仓库满员了喜欢请支持一下
目录
前言
二叉搜索树具有以下重要特性:
- 左子树上所有节点的值都小于它的根节点的值
- 右子树上所有节点的值都大于它的根节点的值
- 左右子树也必须是二叉搜索树
这种数据结构在实际开发中有广泛应用场景,比如:
- 数据库索引的实现
- 文件系统的目录结构
- 内存管理中的内存分配算法
- 游戏开发中的场景管理、
根据二叉树创建字符串
思路:
左边为空,右不为空,不能省略空括号;其余情况下空均可以省略空括号
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
string tree2str(TreeNode* root)
{
string str;
if(root==nullptr)
return str;
str+=to_string(root->val);
//特殊情况处理
//左不为空需要递归获取子树
//左为空,右不为空,左边的括号需要保留
if(root->left!=nullptr||root->right!=nullptr)
{
str+='(';
str+=tree2str(root->left);
str+=')';
}
//右不为空需要递归获取子树
//右为空任何情况下都不需要括号
if(root->right!=nullptr)
{
str+='(';
str+=tree2str(root->right);
str+=')';
}
return str;
}
};拓展:to_string函数的介绍
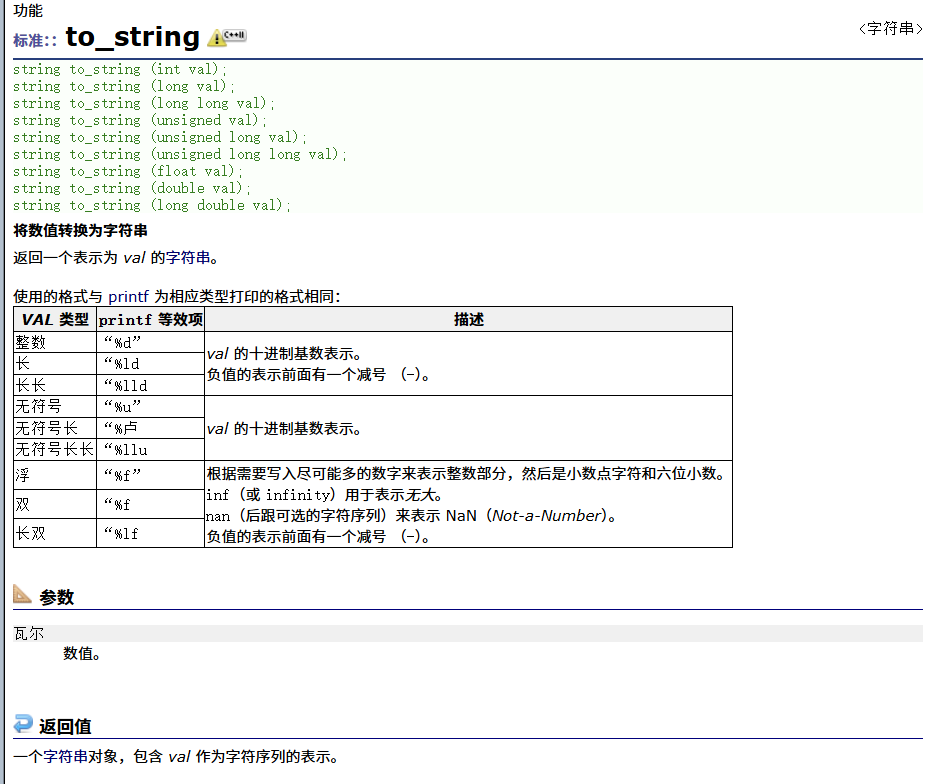
核心作用与规则:
-
参数要求(遵循"右不为空"原则):
-
必须 在括号内提供数值参数(
int/double/long等) -
空括号
to_string()❌ 违反规则(编译错误) -
无参数版本不存在 ❌
-
-
返回值(遵循"左边为空"原则):
-
总是返回新的
std::string对象 -
返回值不能忽略(必须接收或使用)
-
类型转换规则:
| 输入类型 | 输出示例 | 特殊规则 |
|---|---|---|
int 123 |
"123" |
直接转换 |
double 3.14 |
"3.140000" |
默认补足6位小数 |
bool true |
❌ 不支持 | 需手动转换 |
char 'A' |
"65" (ASCII值) |
非字符转换,需用string(1,'A') |
stoi函数的介绍
二叉树的层序遍历
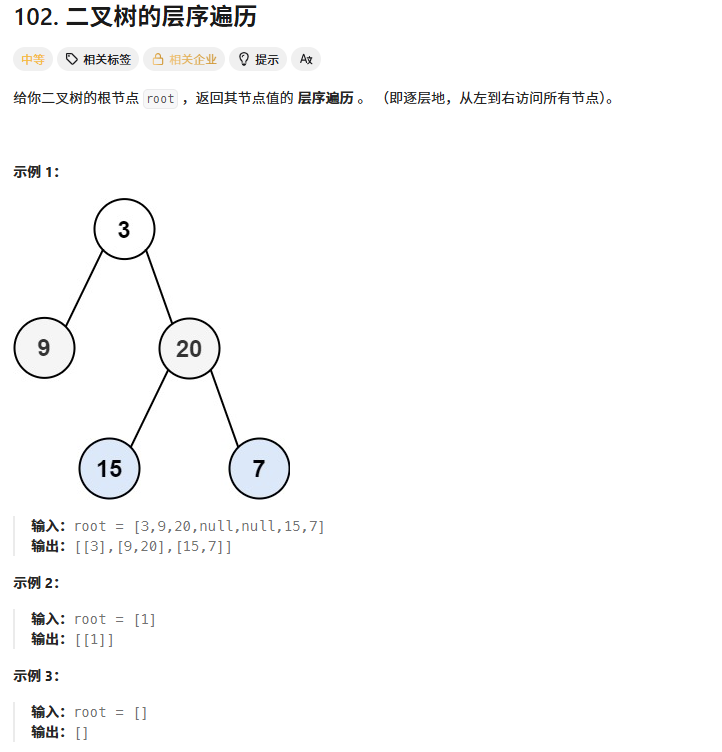
思路1:双队列。队列1存节点指针,队列2存节点层数。记录每个节点的层数。
当前节点的孩子层数+1.
思路2:层序遍历的时候添加一个遍历levelsize,记录每一层的数据个数。树不为空的情况下,第一层levelsize=1,循环控制结束后第一层出完了第二层进队列。队列中size就是第二层的数据个数。以此类推,假设levelsize是第n层个数,因为层序遍历思想为当前层节点出队列,带入下一层节点(子节点),循环控制第n层出完了,第n+1节点也就进队列了。队列size就是下一层的levelsize。
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root)
{
queue<TreeNode*>q;
int levelsize=0;//记录当前层数多少个数据
if(root)
{
q.push(root);
levelsize=1;
}
vector<vector<int>>vv;
//层序遍历
while(!q.empty())
{
vector<int>v;
//控制一层一层出
while(levelsize--)
{
TreeNode*front=q.front();
q.pop();
v.push_back(front->val);
if(front->left)
{
q.push(front->left);
}
if(front->right)
{
q.push(front->right);
}
}
vv.push_back(v);
//当前层出完了下一层节点都进队列,队列数据个数就是下一次节点个数
levelsize=q.size();
}
return vv;
}
};二叉树的层序遍历2
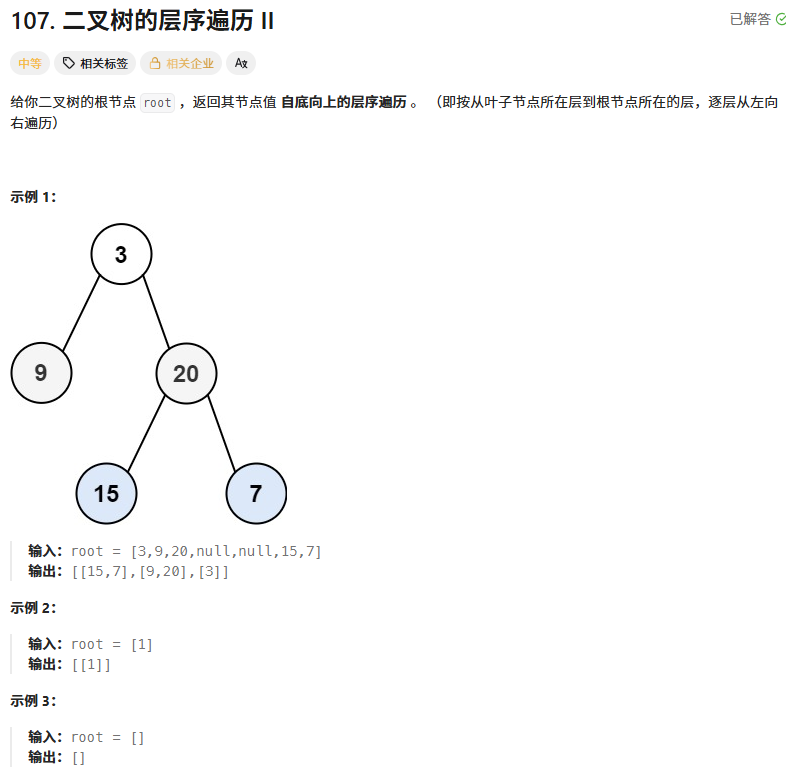
相比于前一题逆置一下
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root)
{
//思路2
vector<vector<int>>vv;
queue<TreeNode*> q1;
int levelsize=0;
if(root)
{
q1.push(root);
levelsize=1;
}
while(levelsize>0)
{
//控制一层一层出
vector<int>v;
while(levelsize--)
{
TreeNode*front=q1.front();
q1.pop();
v.push_back(front->val);
//下一层的孩子入队列
if (front->left)
q1.push(front->left);
if (front->right)
q1.push(front->right);
}
vv.push_back(v);
//当前层出完了,下一层都进队列了
//q.size()就是下一层节点个数
levelsize=q1.size();
}
//相比于前一题逆置一下
reverse(vv.begin(),vv.end());
return vv;
}
};二叉树的最近公共祖先

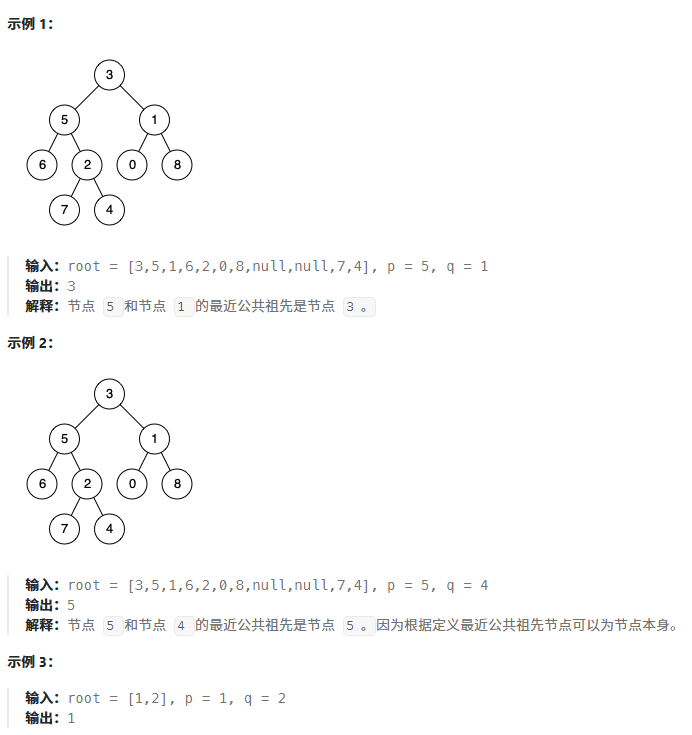
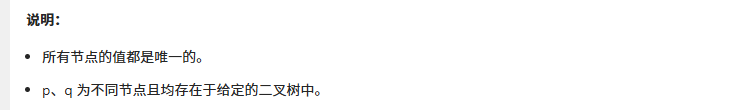
算法一:
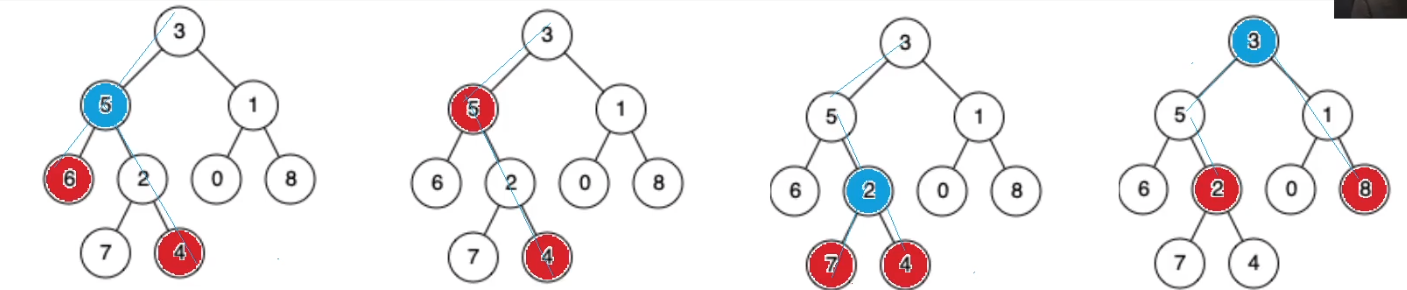
思路: 观察我们发现两个节点的公共祖先必须保证一个在祖先的左侧一个在祖先的右侧。如果都在同一侧则不需要找另一侧。比如下图的左侧只需要找左子树,右图只需要找右子树。
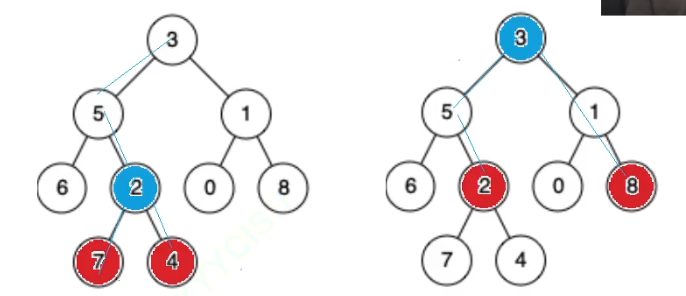
cpp
class Solution
{
public:
//算法一:
//时间复杂度O(N^2)
bool IsInTree(TreeNode* root,TreeNode* x)
{
if(root==nullptr)
return false;
//相等肯定在树上
return root==x||IsInTree(root->left,x)||IsInTree(root->right,x);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
{
//空树不需要找
if (root == nullptr)
return nullptr;
//要找的节点自己就是二叉树根节点
if (root == p || root == q)
return root;
bool pInleft = IsInTree(root->left, p);
bool pInright = !pInleft;
bool qInleft = IsInTree(root->left, q);
bool qInright = !qInleft;
//p和q在二叉树两侧,root就是公共祖先
//都在左去左子树查找
//都在右去右子树查找
if ((pInleft && qInright) || (pInright && qInleft))
{
return root;
}
//要么都左要么都右
else if (pInleft && qInleft)
{
return lowestCommonAncestor(root->left, p, q);
}
//写法1:
else if (pInright && qInright)
{
return lowestCommonAncestor(root->right, p, q);
}
return nullptr;
//写法2:
// else
// {
// return lowestCommonAncestor(root->right,p,q);
// }
}
};但是实际上这种算法时间复杂度过高,仅作为参考
算法二:
如果求出两个节点到根的路径,则可以转化为链表相交的问题。
如:6到3 的路径为6-》5-》3。4到3的路径为-》2-》5-》3。
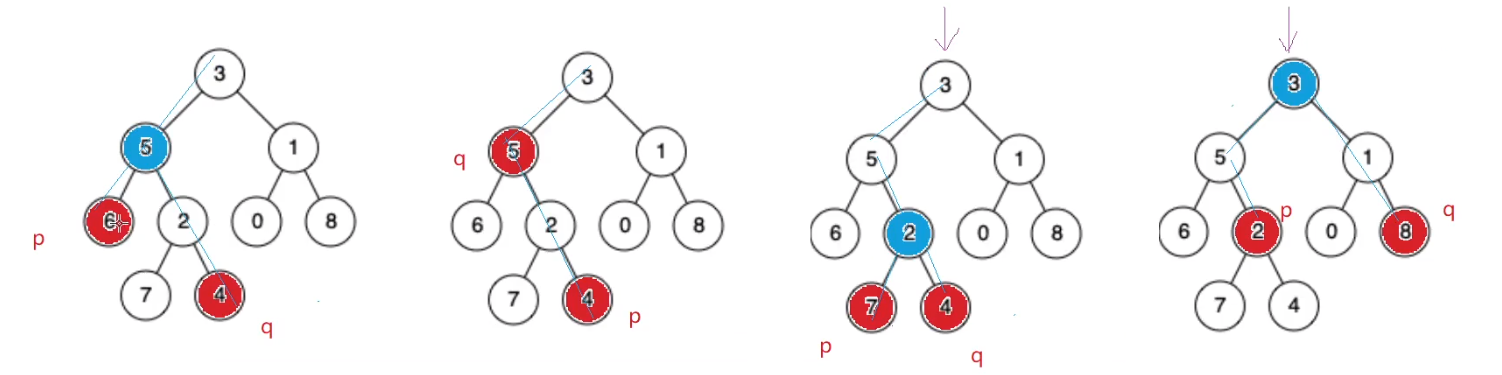
则可以利用前序遍历的思路找x节点的路径。遇到root先入栈,因为root不是x,但是root可能是分支节点。
本质上就是前序查找+栈记录查找路径
如果左右子树都没有x,则说明root不是根-》x的路径,所以要pop出栈,回退去其他分支查找。
cpp
class Solution
{
public:
//算法2:
//深度遍历的层序查找,用栈记录路径
bool GetPath(TreeNode*root,TreeNode* x,stack<TreeNode*>& path)
{
//空树没有路径
if(root==nullptr)
return false;
path.push(root);
//经过路径
if(root==x)
return true;
//如果不再公共节点上
//左子树去找
if(GetPath(root->left,x,path))
return true;
//右子树去找
if(GetPath(root->right,x,path))
return true;
//如果都不在那就不在路径上
path.pop();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
{
stack<TreeNode*>pPath,qPath;
GetPath(root,p,pPath);
GetPath(root,q,qPath);
//找交点
while(pPath.size()!=qPath.size())
{
//长的先走
if(pPath.size()>qPath.size())
{
pPath.pop();
}
else
{
qPath.pop();
}
}
//在同时走找交点
while(pPath.top()!=qPath.top())
{
pPath.pop();
qPath.pop();
}
return pPath.top();
}
};将二叉搜索树转化为排序的双向链表

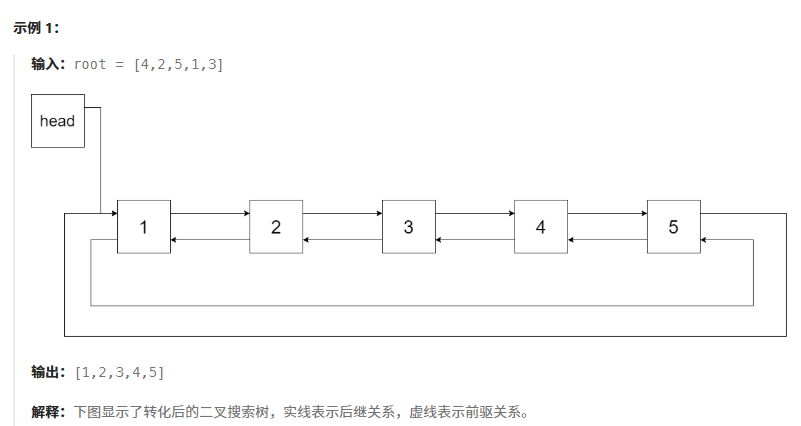
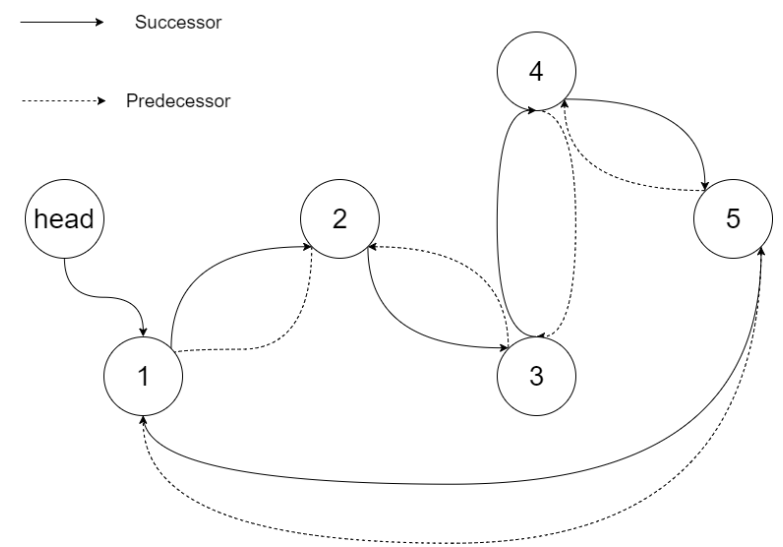

思路1:中序遍历二叉树,遍历顺序是有序的,将节点放到vector中,再将链表前后节点关系进行修改。
思路2:中序遍历二叉树,遍历顺序是有序的,遍历过程中修改左指针为前驱和右指针为后继。记录一个cur和prev,cur为当前中序遍历的节点,prev为之前中序遍历的节点,cur->left指向prev,cur->right无法指向中序的下一个,因为不知大中序下一个是谁,但是prev->right指向cur。也就是说每个结点的左是在遍历到当前节点的时候修改为前驱的,节点的右是遍历到下一个节点的时候修改指向后继的。
cpp
class Solution
{
public:
//当前的中序遍历
void InOrderConvent(Node*cur,Node*&prev )
{
if(cur==nullptr)
return ;
InOrderConvent(cur->left,prev);
//cur中序遍历
//cur指向前一个变成前驱
cur->left=prev;
//前一个结点的后继
if(prev)
{
prev->right =cur;
}
prev=cur;
InOrderConvent(cur->right,prev);
}
Node* treeToDoublyList(Node* root)
{
if(root==nullptr)
return nullptr;
Node*prev=nullptr;
InOrderConvent(root,prev);
Node*head=root;
while(head->left)
{
head=head->left;
}
//循环链表
head->left=prev;
prev->right=head;
return head;
}
};从前序与中序遍历序列构造二叉树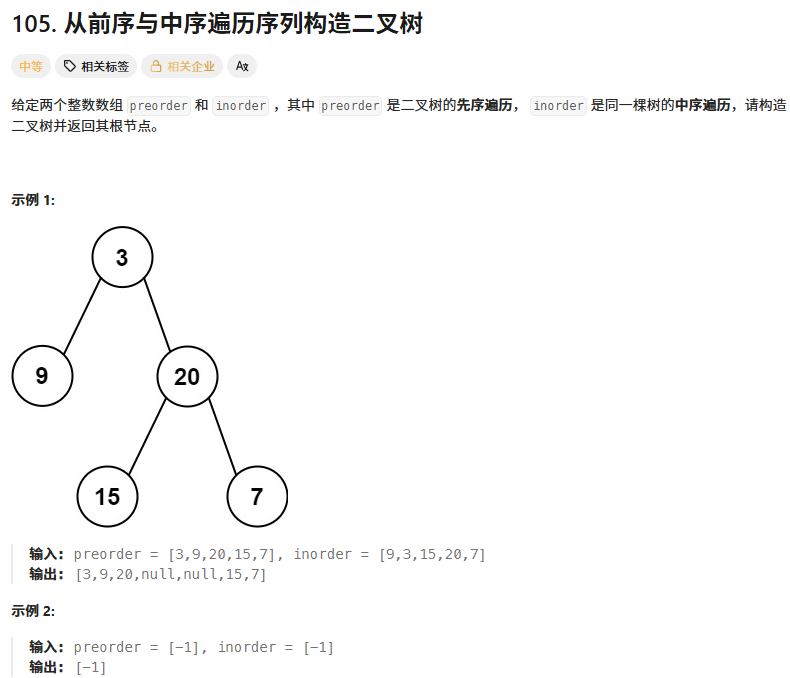
思路:前序确定跟,中序分割出左右子树。
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//prei:前序区间
TreeNode* build(vector<int>& preorder, vector<int>& inorder,int&prei,int Inbegin,int Inend)
{
//不存在的区间
if(Inbegin>Inend)
return nullptr;
//前序遍历确定跟
TreeNode* root=new TreeNode(preorder[prei]);
//中序分隔左右子树
int rooti=Inbegin;
while(rooti<=Inend)
{
//找到了
if(preorder[prei]==inorder[rooti])
{
break;
}
else
{
rooti++;
}
}
prei++;
//分隔为三段[Inbegin,rooti-1] rooti [rooti+1,Inend]
//构建左子树
root->left=build(preorder,inorder,prei,Inbegin,rooti-1);
//构建右子树
root->right=build(preorder,inorder,prei,rooti+1,Inend);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder)
{
int i=0;
return build(preorder,inorder,i,0,inorder.size()-1);
}
};二叉树前序非递归


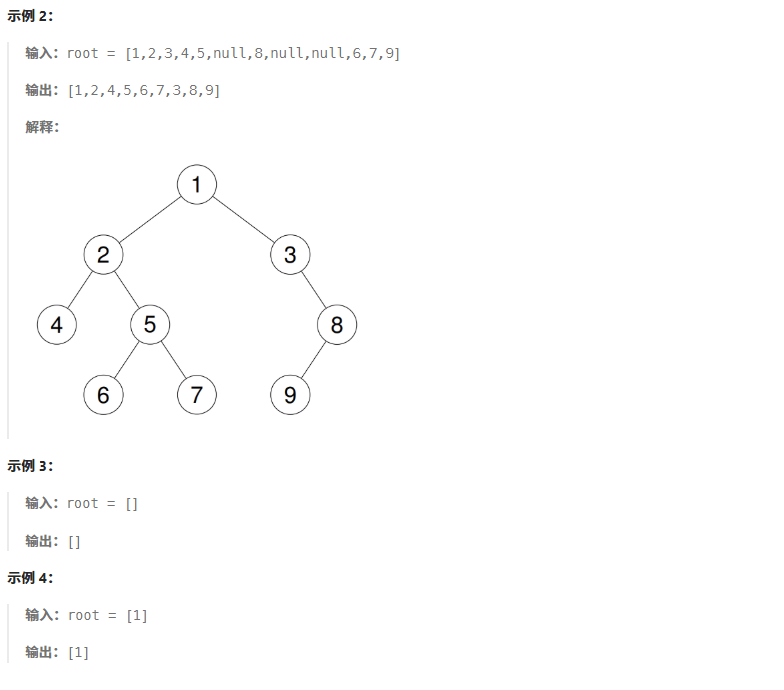
二叉树的递归遍历虽然写法简单,但是因为递归需要开栈帧,如果二叉树深度比较深那么可能导致栈溢出,所以需要非递归写法。
非递归实现思想
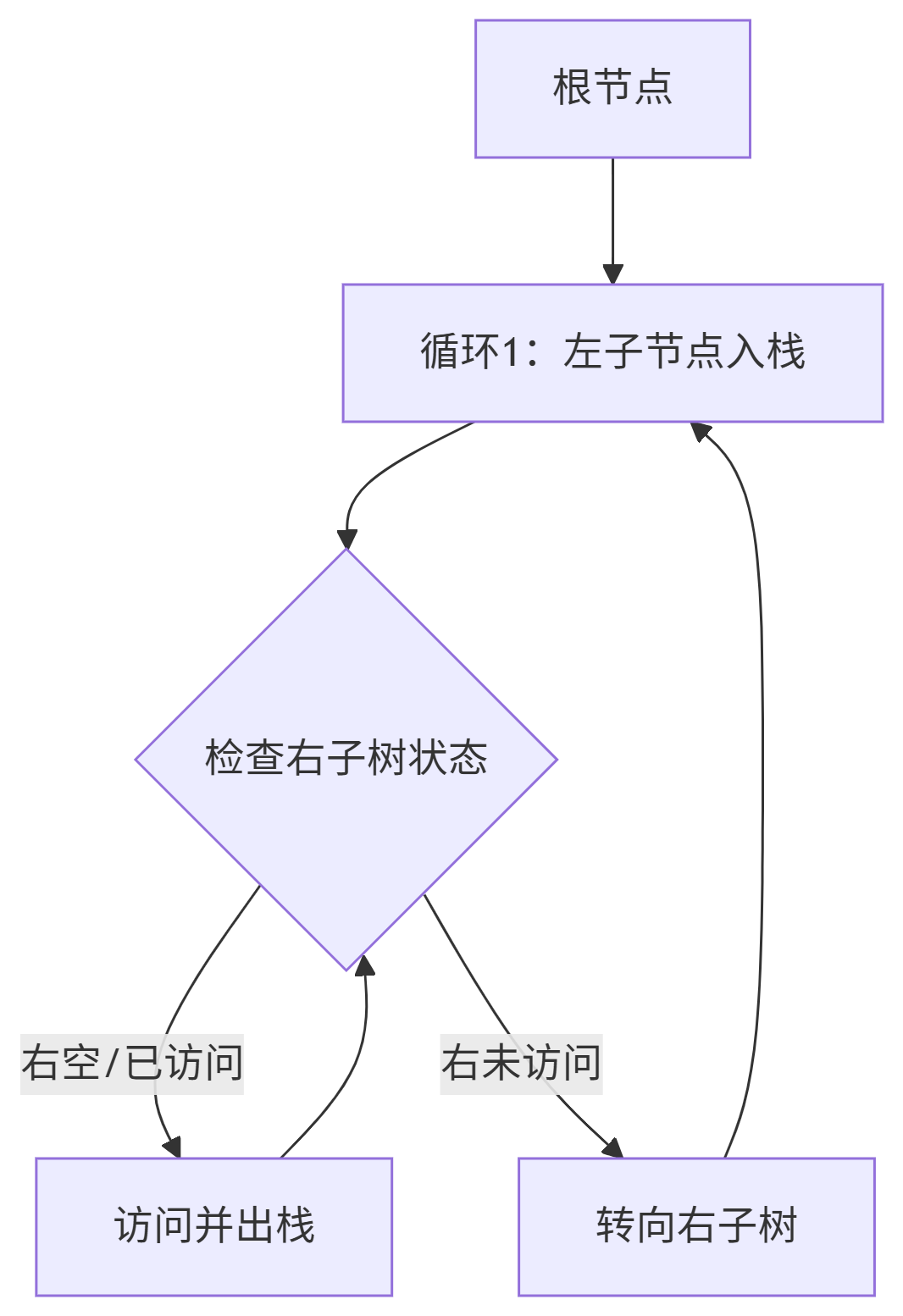
要迭代⾮递归实现⼆叉树前序遍历,⾸先还是要借助递归的类似的思想,只是需要把结点存在栈中, ⽅便类似递归回退时取⽗路径结点。
跟这⾥不同的是,这⾥把⼀棵⼆叉树分为两个部分:
-
先访问左路结点
-
再访问左路结点的右⼦树
这⾥访问右⼦树要以循环从栈依次取出这些结点,循环⼦问题的思想访问左路结点的右⼦树。
中序和后序跟前序的思路完全⼀致,只是前序先访问根还是后访问根的问题。
后序稍微⿇烦⼀些,因 为后序遍历的顺序是左⼦树右⼦树根,当取到左路结点的右⼦树时,需要想办法标记判断右⼦树是否 访问过了,如果访问过了,就直接访问根,如果访问过需要先访问右⼦树
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root)
{
stack<TreeNode*>st;
TreeNode*cur=root;
vector<int>v;
while(cur||!st.empty())
{
//循环开始代表访问一棵树的开始
//先访问左路结点,左路结点入栈
while(cur)
{
v.push_back(cur->val);
st.push(cur);
cur=cur->left;
}
//依次取左路节点右子树出来访问
TreeNode*news=st.top();
st.pop();
//子问题的方式访问右子树
//循环子问题
cur=news->right;
}
return v;
}
};二叉树中序非递归

cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),right(right){}
* };
*/
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
stack<TreeNode*> st; // 辅助栈:存储待回溯的节点
TreeNode* cur = root; // 当前遍历节点(初始为根节点)
vector<int> v; // 存储遍历结果
// 当存在未处理节点或栈非空时继续遍历
while (cur || !st.empty()) {
// 阶段1:深度优先访问左子树
// 将当前节点和所有左子节点入栈(直到叶子节点)
while (cur) {
st.push(cur); // 当前节点入栈(后续回溯用)
cur = cur->left; // 持续向左深入
}
// 阶段2:回溯处理根节点
TreeNode* top = st.top(); // 获取栈顶节点(当前最左节点)
st.pop(); // 弹出已访问节点
v.push_back(top->val); // 访问节点值(相当于处理根节点)
// 阶段3:转向右子树
// 将当前指针设为右子节点(若存在右子树则进入下一轮循环处理)
cur = top->right; // 关键:以右子树为新的起点继续遍历
}
return v;
}
};二叉树后序非递归


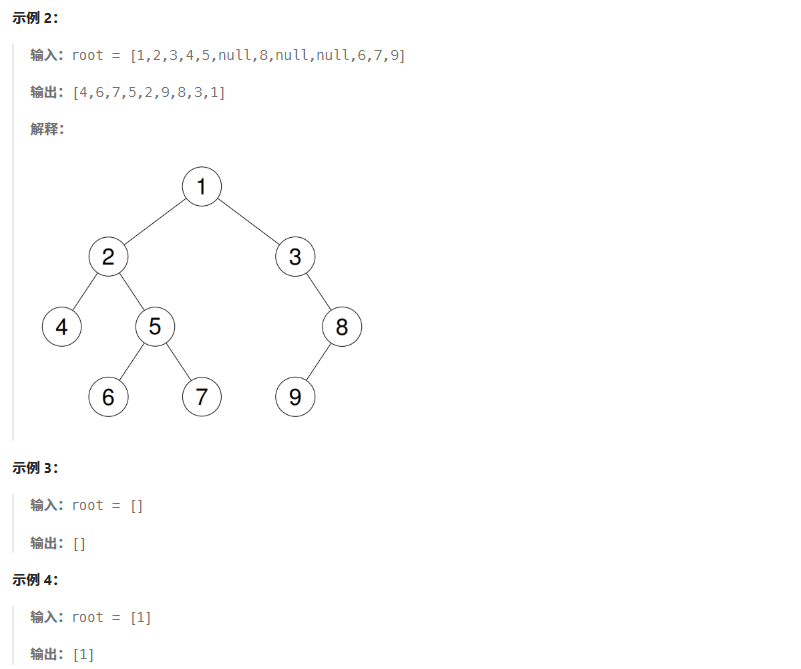
取到一个左路结点的时候左子树已经访问过了;如果左路结点右子树不为空,右子树没有访问,则上一个访问的是左子树的根;如果左路结点右子树不为空,右子树已经访问,则上一个访问的是右子树的根
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
stack<TreeNode*> st; // 辅助栈:存储待回溯的节点
TreeNode* cur = root; // 当前遍历节点(初始为根节点)
TreeNode* prev = nullptr; // 记录前次访问的节点(关键:判断右子树是否已访问)
vector<int> v; // 存储遍历结果
while (cur || !st.empty()) {
// 阶段1:深度优先访问左子树
// 将当前节点和所有左子节点入栈(直到叶子节点)
while (cur) {
st.push(cur);
cur = cur->left; // 持续向左深入
}
// 获取栈顶节点(此时左子树已访问完)
TreeNode* top = st.top();
/* 关键判断:何时可以访问当前节点?
条件1:右子树为空(无右子树)
条件2:右子树已被访问(prev == top->right)
满足任一条件即可访问当前节点 */
if (top->right == nullptr || top->right == prev) {
v.push_back(top->val); // 访问节点值
st.pop(); // 弹出已访问节点
prev = top; // 更新前次访问节点(标记为已处理)
}
// 右子树存在且未访问
else {
cur = top->right; // 转向右子树(以相同逻辑处理右子树)
prev = nullptr; // 重置prev(可选,逻辑已隐含)
}
}
return v;
}
};本期算法题分享到此结束,如果你喜欢请点个赞关注支持一下,谢谢