人脸识别之--计算余弦相似度-android

余弦相似度是比对两个向量是否一致，余弦相似度是通过计算两个向量的夹角余弦值来衡量它们之间的相似度，算出来的值可以直接用作相似度的分数。

公式：

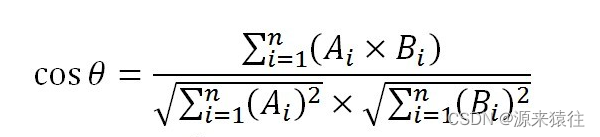
余弦相似度和欧式距离经常用来人脸识别特征对比。

其中：

1、余弦相似度是通过计算两个向量的夹角余弦值来衡量它们之间的相似度

2、欧式距离是通过计算两个向量之间的欧氏距离来衡量它们之间的相似度

• 余弦相似度的优点是在计算相似度时不受向量的绝对大小影响，只受向量的方向影响，因此适用于文本、图像等数据的相似度度量。
• 欧式距离的优点是直观易理解，计算简单。但是欧式距离在计算高维稀疏数据时可能会受到维度灾难的影响，且对异常值敏感。

在人脸识别中余弦距离用的比较多。

这里用来计算两组特征值的相似度，具体代码如下：

package com.hax.util;

import com.hax.vo.FaceInfo;

import java.util.List;

/**
 * add hmy
 * 人脸比对工具
 * 2024年6月12日16:34:22
 */
public class FaceUtils {

    // 计算平方值
    private static double euclideanNorm(double []vec) {
        double sum = 0.0;
        for (int i =0; i < vec.length; i++){
            sum += vec[i] * vec[i];
        }
        return Math.sqrt(sum);
    }
    // 计算平方值
    private static double euclideanNorm(List<Float> vec) {
        double sum = 0.0f;
        for (int i =0; i < vec.size(); i++){
            sum += vec.get(i) * vec.get(i);
        }
        return Math.sqrt(sum);
    }
    // 计算两个向量的点积
    private static double dotProduct(double[] vec1,double[] vec2) {

        double result = 0.0;
        for (int i = 0; i < vec1.length; ++i) {
            result += vec1[i] * vec2[i];
        }

        return result;
    }
    // 计算两个向量的点积
    private static double dotProduct(List<Float> vec1, List<Float> vec2) {

        double result = 0.0f;
        for (int i = 0; i < vec1.size(); ++i) {
            result += (vec1.get(i) * vec2.get(i));
        }

        return result;
    }
    //计算余弦相似度 返回具体分值
    public static double verification(FaceInfo src, FaceInfo dest) {
        double sim = dotProduct(src.getEmbed(), dest.getEmbed()) /
                (euclideanNorm(src.getEmbed()) * euclideanNorm(dest.getEmbed()));

        sim = 0.5 + sim * 0.5;//把-1到1的范围 隐射到0-1的范围 -1到0 映射0-0.5 0到0.5隐射到0.5-0.75 0.5到1 映射到0.75-1

        return sim;
    }
}

其中Embed值是List<Float> 值为512维。