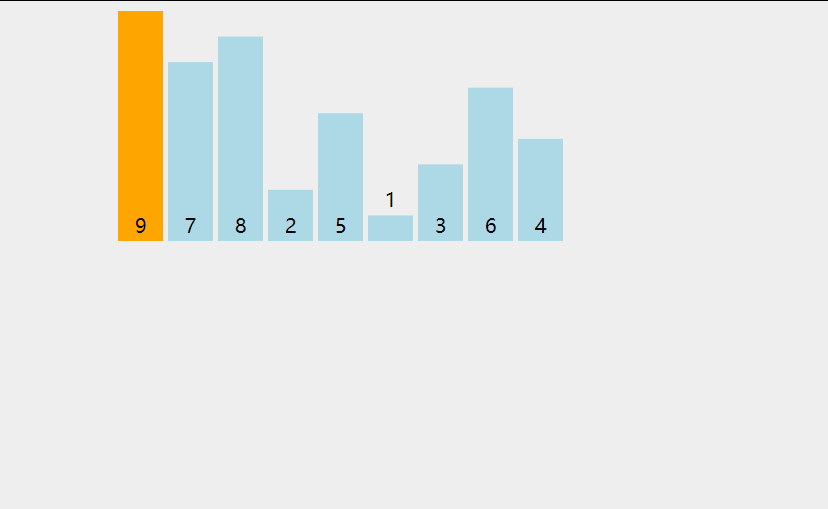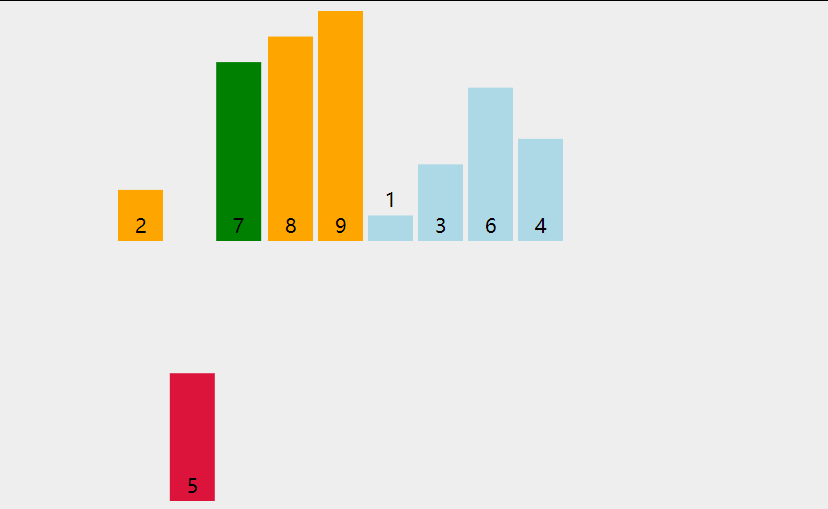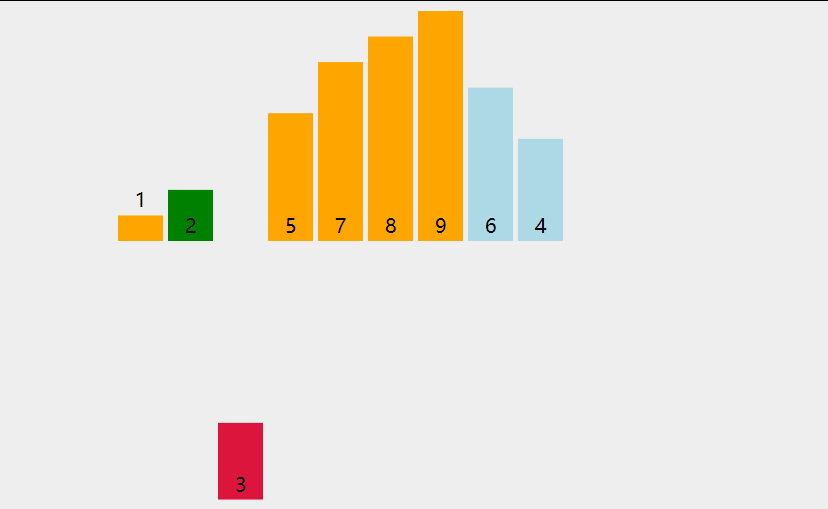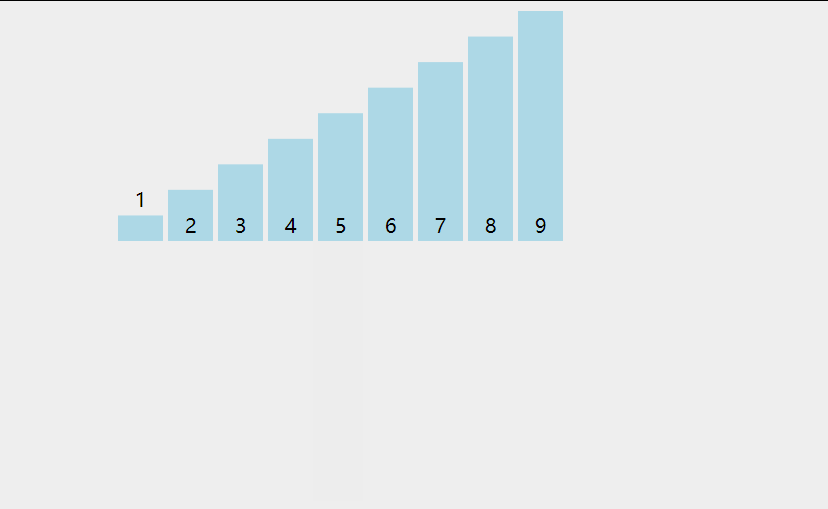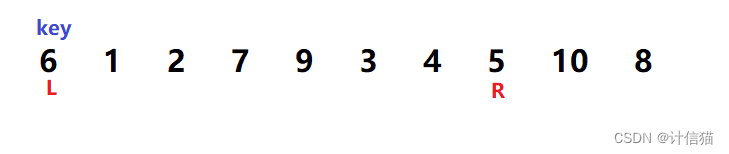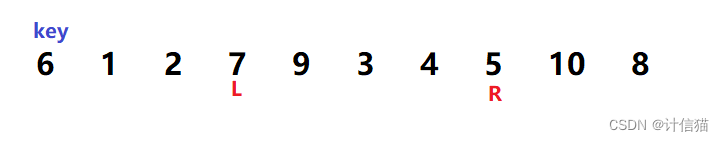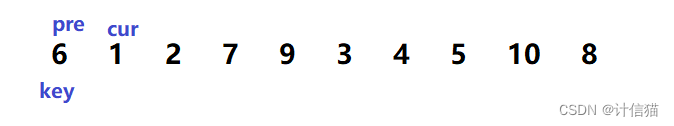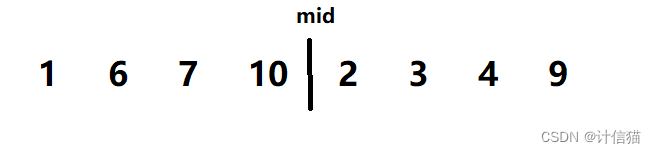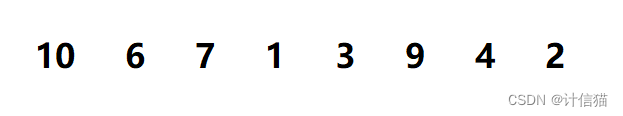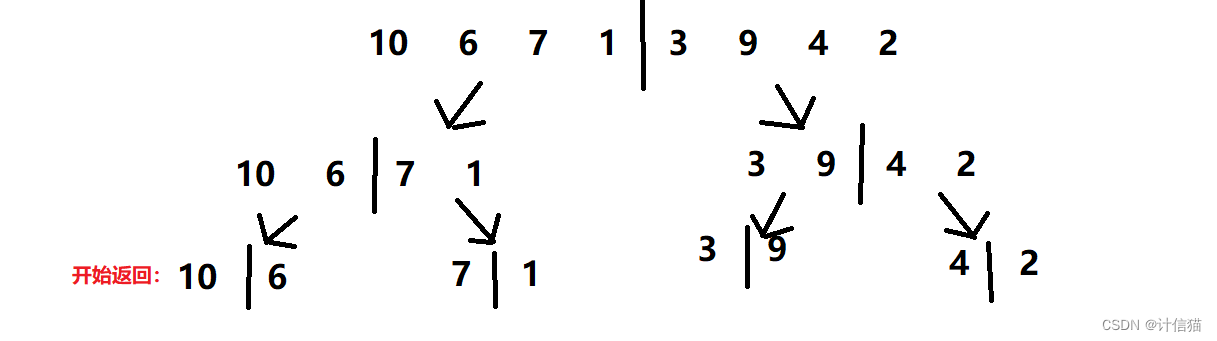数据结构——排序

引言： 在某宝上，当我们以价格升序或者降序来选择商品时，是什么让数以上百万件商品 整齐地按照价格排成一列？当我们搜索中国大学排名时，又是哪种算法将中国的大学由高到低 进行排列？

而问题的答案就可以在本篇博客中找到。在本篇博客中，我们将学到各种排序方法，它们有的虽然处理不了大量的数据 ，但具有着教学意义 ，给予我们灵感；有的虽然十分复杂 ，难以理解 ，但秒杀上百万的数据不在话下。现在就让我们一起进入数据结构------排序的学习吧！

更多有关C语言和数据结构的知识详解可前往个人主页：计信猫

一，插入排序

1，直接插入排序

直接插入排序是一种简单的插入排序法 ，它的基本思想 是将一个数直接插 入一个原本就已经有序的序列 中，直到要插入的数据全部被插入序列 之后，那么就可以得到一个新的有序序列。

所以它的排序方式 也可以用如下动图表示：

所以我们可以先将数组的首元素（单个元素） 看为一个有序序列 ，然后我们再用数组第二个元素 进行插入，完成插入之后，那么数组的前两个元素 就变成了一个有序序列 ，然后我们再进行后续元素的插入 ，直到整个数组的元素 都全部被插入 之后，那么我们就得到了一个新的有序序列 。那么我们的直接插入排序的代码入下：

cpp 复制代码

//直接插入排序
void InsertSort(int* a, int n)
{
	int end = 0;
	int tmp = 0;
	for (int i = 0; i < n - 1; i++)
	{
		//a[0]到a[end]为一个有序序列，将a[end+1]的值插入有序序列中
		end = i;
		//将要插入的值，即a[end+1]记录给tmp
		tmp = a[end + 1];
		while (end >= 0)
		{
			if (tmp < a[end])
			{
				//如果值大于tmp，则将这个数往后移动一位
				a[end + 1] = a[end];
				--end;
			}
			else
			{
				break;
			}
		}
		/*跳出循环两种可能：1，end为 - 1，说明tmp为最小的数，则将a[0]赋值为tmp
						   2，break跳出，则说明找到插入的位置*/
		a[end + 1] = tmp;
	}
}

2，希尔排序

希尔排序是一种高效的，但同时也是十分复杂抽象的排序方式，它的底层逻辑还是会运用到我们前面所学到的直接插入排序。而它主要分为两个步骤：

1，预排序，让数组接近于有序

2，直接插入排序，让数组有序

那就让我们以以下的无序序列进行举例吧！

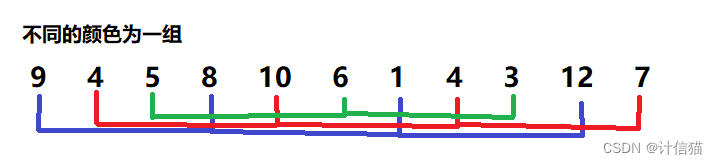
首先我们进行预排序。它的具体操作其实就是首先定义一个整型变量gap ，将数组每隔**（gap-1）个元素** 分为一组，然后再对每个组分别进行插入排序，使整个数组接近有序。假定我们的gap值为3，那么试例序列就可以被分为如下组：

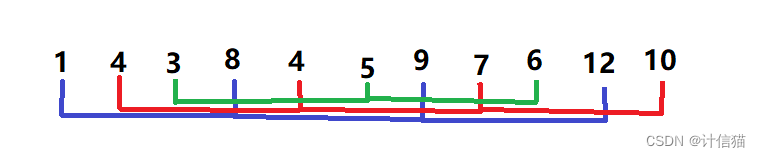
那么现在让我们对每个组分别进行**直接插入排序，**那么所得到的序列如下：

通过此图我们是否就可以看出，该序列已经开始逐渐接近于有序 了呢？之后我们再继续对gap 进行调整，后再此进行以上的预排序，那么序列就会一次比一次更加接近有序 。最后当gap 调整为1 的时候，那么不就是我们所学到的直接插入排序了吗？那么直接插入排序之后，整个序列就彻底变为一个有序序列了！

当然，希尔排序比较复杂，它的效率优势也只有在数据量庞大的时候才可以体现出来，并且它的效率与gap的取值息息相关。

●gap越大，那么序列中大的数就可以越快地调整到序列的后端，小的数就可以越快地调整到序列的前端，但整个序列越不会接近于有序

●gap越小，那么序列中大的数就会越慢地调整到序列的后端，小的数就会越慢地调整到序列的前端，但整个序列越接近于有序

●gap为1时就相当于直接插入排序

而关于gap 的取值则是世世代代数学家们一直在争论的问题，但目前比较主流的取值方式如下：

●（赋值部分）gap=n;(n为序列元素总个数)

● (调整部分) gap=gap/3+1;

那么，我们的希尔排序的代码如下：

cpp 复制代码

//希尔排序
void ShellSort(int* a, int n)
{
	int gap = n;
	int end = 0;
	int tmp = 0;
	while (gap > 1)
	{   //对gap进行调整
		//+1是为了保证最后一次gap为1
		gap = gap / 3 + 1;
		for (int i = 0;i < n - gap ; i++)//i<n-gap是为了防止溢出
		{
			//gap>1为预排序，gap=1为直接插入排序
			end = i;
			tmp = a[end + gap];
			while (end >= 0)
			{
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}

二，选择排序

1，直接选择排序

直接选择排序是一种简单的选择排序算法 ，它的基本思想 是在一段序列中同时选择出序列中最小和最大的元素 ，并且将最小的元素 与序列队首 交换，最大的元素 与序列队尾 交换，然后缩小序列范围继续进行以上操作 ，直至序列中只有一个元素。

所以直接选择排序也可以使用如下的动图所表示：

故我们可以向后遍历数组 ，找出数组中的最大值 和最小值 并且放于数组的头与尾 ，然后再将遍历范围 去除数组的头与尾 ，再进行以上操作，直至遍历范围只剩下一个元素即可。

那么我们的直接选择排序的代码入下：

cpp 复制代码

//交换函数
void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}
//直接选择排序
void SelectSort(int* a, int n)
{
	int begin = 0;
	int end = n - 1;
	while (begin < end)
	{
		int min = begin;
		int max = end;
		//首先将序列两端比较，确保序列的开头一定小于序列的结尾
		if (a[begin] > a[end])
		{
			Swap(&a[begin], &a[end]);
		}
		//再次对序列中进行比较，找出最大和最小值所对应的下标
		for (int i = begin + 1; i <= end; i++)
		{
			if (a[i] > a[max])
			{
				max = i;
			}
			if (a[i] < a[min])
			{
				min = i;
			}
		}
		//将最大和最小值放于序列头和尾
		Swap(&a[min], &a[begin]);
		Swap(&a[max], &a[end]);
		begin++;
		end--;
	}
}

2,堆排序

堆排序也是一种及其强大的排序方式，而这种方法我已在前面的博客中进行了及其详细的讲解，在这里就不再赘述了，这里是堆排序的博客链接：堆排序。

三，冒泡排序

冒泡排序是在我们所学到的排序方式当中最简单的一个 ，具有着独特的教学启蒙意义。它的排序方式如下所示：

由图中我们可以清楚的看出：每当进行一趟排序时，都会将相邻的两个数据进行比较 ，如果前一个数据较大，那么它就和后一个数据交换位置 ，反之就不用交换位置。而每当一趟冒泡排序完成时，那么这个所排序的区间中最大的数就会沉底。所以冒泡排序的代码如下：

cpp 复制代码

//冒泡排序
void BubbleSort(int* a, int n)
{
	for (int i = 0; i < n - 1; i++)
	{
		int count = 0;
		int j = 0;
        //每一趟冒泡排序代码
		for (j = 0; j < n - i - 1; j++)
		{
            //交换数据
			if (a[j] > a[j + 1])
			{
				int tmp = a[j];
				a[j] = a[j + 1];
				a[j + 1] = tmp;
				count = 1;
			}
		}
        //如果一趟排序中没有数据进行交换，那么该数列就已经有序
		if (count == 0)
		{
			break;
		}
	}
}

四，快速排序

快速排序算得上是排序当中数一数二的佼佼者 了，它的高效率为它奠定了举足轻重的地位。在面试当中快速排序也是一个常考的知识点 ，所以为了将这个重要的知识点讲清楚将透彻，我会一步一步地讲解快速排序，并且讲解快速排序原代码的不足同时对代码进行改装、优化和升级 。希望大家可以仔细阅读这部分内容，因为快速排序真的非常重要！！

1，快速排序

Ⅰ，基本思想

基本思想：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

当然，干巴巴的文字肯定非常抽象，那么我们以如下无序序列进行举例：

首先，我们就需要确定一个基准值------key（我们一般以序列最左边的值------6的下标为key） ，然后我们定义待排序序列 中队首为L（即Left） ，队尾为R（即Right）。那么我们的待排序序列可变为如下情况：

此时，我们就先将R 向左移动。只要R 指向的值比key 值大，就一直向左移动，直到R 所指向的值小于key。那么经过移动之后，R 就会停在5 的地方，如下图所示：

当R 停下之后，我们就需要再对L 进行移动，而L 的移动方式恰好与R 相反。只要L 指向的值比key 值小，就一直向右移动，直到L所指向的值大于key。经过移动之后，L 就会停在7的地方，如下图所示：

当L 与R 都移动完成停下之后，我们就将L 与R 对应的值进行交换，交换完成之后如下图所示：

交换完成后，我们就再次进行 以上的三部分操作，如下图所示：

此时，在L 移动的过程中，L 就与R 相遇了，此时L 就停止移动，并且将L 与R 相遇时所对应的值与key 值交换。那么交换之后就如下图所示：

那么，我们仔细观察现在的图片，比key值小的数是不是全部都在key的左边，比key****值大的数是不是全部都在key的右边了呢？答案是肯定的。所以我们就通过这个方法，就完成了快速排序的四分之三了。

最后，我们就只需要采用相同的思路 ，key****左边和右边的序列 再一次的进行以上的排序方式，不停递归函数 ，直到序列为空 或者序列中只有一个元素 的时候，那么就可以停止递归调用， 这时候整个序列就被排序为有序序列了。

Ⅱ，代码实现

有了上面基本思想的讲解，我们就可以进行快速排序 的代码实现了。为了确保函数的边界不会轻易被改变，我们将再定义两个变量begin和end 分别代替L 和R 来对序列进行遍历。所以我们的快速排序代码如下所示：

cpp 复制代码

//快速排序
void QuickSort(int* a, int left, int right)
{
	if (left >= right)//当序列为空或者只有一个元素就停止递归
	{
		return;
	}
	int key = left;
	int begin = left;
	int end = right;
	while (begin < end)
	{
		//end的值比key大就向左移动，直到end的值比key小或者遇到begin就停止移动
		while (a[end] >= a[key] && begin < end)
		{
			end--;
		}
		//begin的值比key小就向右移动，直到begin的值比key大或者遇到end就停止移动
		while (a[begin] <= a[key] && begin < end)
		{
			begin++;
		}
		//交换begin和end对应的值
		Swap(&a[begin], &a[end]);
	}
	//出循环则表明begin和end相遇
	Swap(&a[key], &a[begin]);
	key = begin;
	//继续使用递归，对[left,key-1]和[key+1,right]进行以上函数的排序
	QuickSort(a , left, key - 1);
	QuickSort(a, key + 1, right);
}

2，快速排序（递归）的优化

Ⅰ,优化一

引出问题：

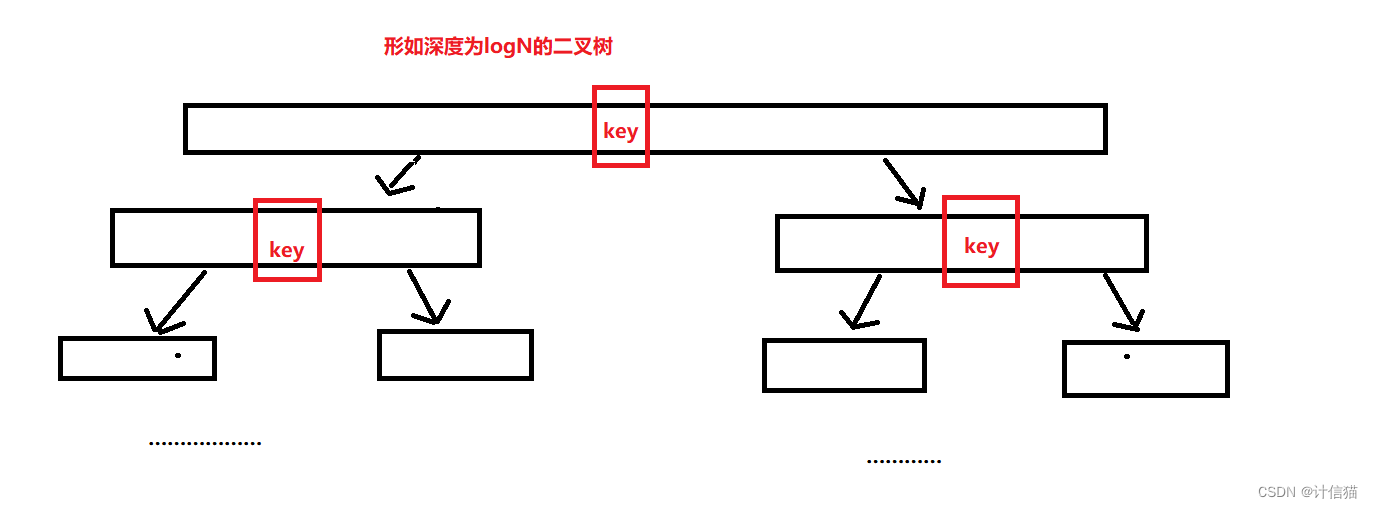
让我们来仔细想一想，key的取值会对整个排序 有什么影响？假设我们取得key值在排序完成后正好位于整个有序序列的中间 ，那我们的快速排序 的递归过程是否可以如下图表示：

所以这一整个过程就可以大致被视为深度为logN 的二叉树 。但假设我们的这个无序序列 是大致有序的（大部分为有序）那么如果我们的key取值在排序完成后正好位于整个有序序列的队首呢？那这个图又会变成什么样呢？

那么此时我们就可以清楚的看出，此时的深度就变为了N ，远远大于logN。所以由此可见，key的取值是能影响快速排序的效率的，如果我们的递归层数过大 ，那么函数就会产生栈溢出的错误，并且算法效率也大幅度降低！！****， 所以key的取值最好的情况为有序序列的中间值 ，这样就完美的避免了大致有序序列递归次数过多的情况。

给出解法：

那么有没有一种方法可以避免上述问题，应对大致有序序列 的情况呢？当然了，我们叫它三数取中法。

三数取中法 的基本思想就是，我们在无序序列 中取出三个数，它们分别为队头，队中，队尾 三个数，我们将三个数中第二大的数的下标取为key值，从而就可以很好的解决我们之前所提到的情况了！所以该方法的代码如下：

cpp 复制代码

//三数取中法
int GetMid(int* a, int left, int right)
{
	int mid = (left + right) / 2;
	if (a[left] > a[mid])
	{
		if (a[mid] > a[right])
		{
			return mid;
		}
		else if (a[right] > a[left])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
	else
	{
		if (a[left] > a[right])
		{
			return left;
		}
		else if (a[right] > a[mid])
		{
			return mid;
		}
		else
		{
			return right;
		}
	}
}

这样，我们就可以将这个函数的返回值 赋值给key，之后我们再将key所对应的值与队首进行互换，于是我们就可以再一次运用之前我们的快速排序函数的代码了，并且大致有序序列的栈溢出问题也得到了完美的改善！

Ⅱ，优化二

提出问题：

让我们来继续仔细思考一个问题，当我们不停的递归 ，直到递归的最后几遍时，那时候每个序列的数据量就已经很小 了，我们还继续使用快速排序这么复杂的函数代码 ，是不是就有一些累赘了。

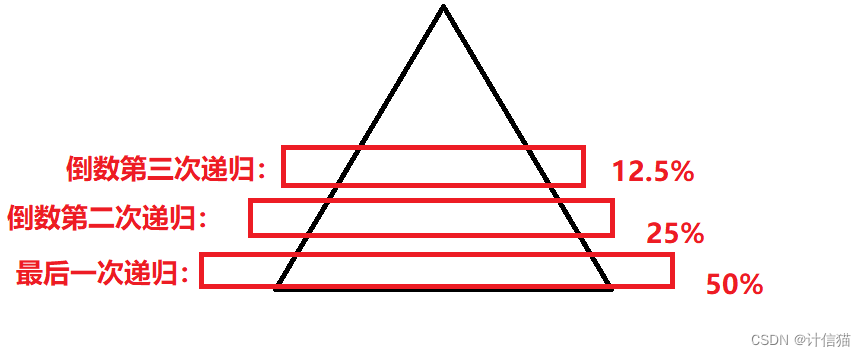
就像之前所提到的，如果我们将快速排序的递归视为一棵二叉树 ，那么我们最后几次递归不就占了整个递归的几乎四分之三了！如下图所示：

所以我们可以在递归的倒数第十次之内，就使用我们之前所学到的插入排序来直接将余下的序列排好！此时插入排序的作用就是进行小区间优化，减少递归次数。

Ⅲ，优化后的代码

所以经过上了两次优化之后，我们的**快速排序（递归）**的优化之后的代码如下：

cpp 复制代码

//快速排序
void QuickSort(int* a, int left, int right)
{
	if (right - left <= 10)
	{
		InsertSort(a + left, right - left + 1);
	}
	else
	{
		if (left >= right)//当序列为空或者只有一个元素就停止递归
		{
			return;
		}
		int mid = GetMid(a, left, right);
	    Swap(&a[left], &a[mid]);
	    int key = left;
		int begin = left;
		int end = right;
		while (begin < end)
		{
			//end的值比key大就向左移动，直到end的值比key小或者遇到begin就停止移动
			while (a[end] >= a[key] && begin < end)
			{
				end--;
			}
			//begin的值比key小就向右移动，直到begin的值比key大或者遇到end就停止移动
			while (a[begin] <= a[key] && begin < end)
			{
				begin++;
			}
			//交换begin和end对应的值
			Swap(&a[begin], &a[end]);
		}
		//出循环则表明begin和end相遇
		Swap(&a[key], &a[begin]);
		key = begin;
		//继续使用递归，对[left,key-1]和[key+1,right]进行以上函数的排序
		QuickSort(a , left, key - 1);
		QuickSort(a, key + 1, right);
	}
}

3，快速排序（递归）------前后指针法

前后指针法其实也是一种排序无序序列 的另一种方法，代码效率其实并没有提高，但是该方法更容易被我们所理解，并且代码也更好写出。

下面我们以如下的例子进行讲解：

首先我们定义两个指针下标 cur与pre ，并和以前一样，我们定数组首元素 为基准值------key。

然后我们对cur 所指向的值与key 指向的值进行比较，如果cur 指向的值小于key 所指向的值，那么就对pre 进行加加操作 ，再交换cur与pre所指向的值，再cur++ 如下图所示：

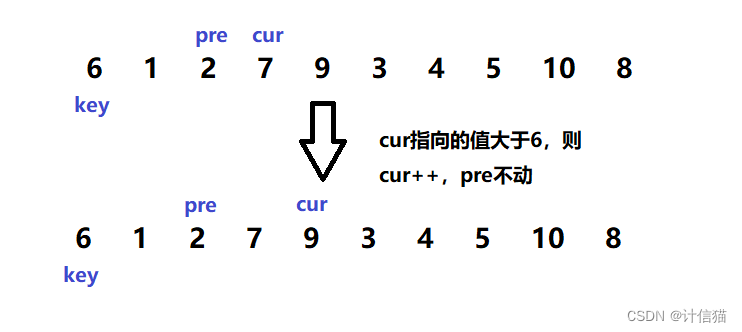
此时cur指向的数字为2 ，小于6 ，故继续以如上方式移动。如果cur 指向的值大于key 所指向的值，则pre 指针不动，cur++。如下图所示：

按照如上操作一直进行下去，然后直到cur超出数组范围时，如下图所示：

此时我们就将pre 与key 的值进行交换，然后再将pre 赋值给key，如下图所示：

怎么样，这个方法是否也达到了前面代码一样的效果了呢？但是这个方法的代码编写却更加的简单！ 虽然不会提高计算机的效率，但是提升了程序员编写代码的效率，又何尝不是一种提升呢？

我们将这新的排序代码封装在一个函数中 ，到时候直接在写快排的时候直接调用就可以了，那么该方法的代码实现如下：

cpp 复制代码

//前后指针法
int partsort2(int* a, int left, int right)
{
	//三数取中法
	int mid = GetMid(a, left, right);
	Swap(&a[left], &a[mid]);
	int key = left;
	int pre = left;
	int cur = left + 1;
	//前后指针法
	while (cur <= right)
	{
		if (a[cur] < a[key] && ++pre != cur)//cur与pre相等，重复交换没意义
		{
			Swap(&a[cur], &a[pre]);
		}
		cur++;
	}
	Swap(&a[pre], &a[key]);
	key = pre;
	return key;
}

所以我们的快速排序就被如此简化：

cpp 复制代码

//快速排序
void QuickSort(int* a, int left, int right)
{
	if (right - left <= 10)
	{
		InsertSort(a + left, right - left + 1);
	}
	else
	{
		if (left >= right)//当序列为空或者只有一个元素就停止递归
		{
			return;
		}
		int key = partsort2(a,left,right);
		//继续使用递归，对[left,key-1]和[key+1,right]进行以上函数的排序
		QuickSort(a , left, key - 1);
		QuickSort(a, key + 1, right);
	}
}

4，快速排序（非递归）

快速排序的递归实现方法我们现在已经学习了，但是，一提到递归，就不得不提到当递归深度过深 时存在的栈溢出问题，那么有没有什么方法，既可以实现快速排序，同时又可以避免栈溢出 的问题呢？答案是肯定的，我们可以使用非递归的方式 实现快速排序的方法。

那我们要如何实现非递归的快速排序呢？这时候我们就需要用到我们之前学到的一个数据结构------栈了。

Ⅰ，思路讲解

那么栈有什么作用呢？栈其实就是用于储存我们需要排序的序列区间的两个端点。假如我们现在有一个长度为10 的无序序列需要进行排序，如下：

那么此时我们需要排序的序列的区间 就为0~9，所以我们就把区间的左右两个端点 放入栈中，如下：（先放右区间再放左区间）

这时候我们就从栈中一次性取出栈顶元素分别赋值给begin和end两个表示排序区间两端的变量 ，然后将将取出的元素从栈中删除。然后我们对该begin和end所指向的序列使用前面学到的方法，进行单趟排序之后，将比key 所指向的值小的放在了key 的左边，比key 所指向的值大的放在了key 的右边。我们假设key 所指向的下标为5，那么结果如下图所示：

那么此时就出现了两对新的区间端点0~4与5~9 ，这时候我们就继续将这两对端点储存进栈中，如下图所示：

那么我们之后就继续进行之前的操作，一次性取出栈的两个顶部元素 表示我们所需要排序的区间 ，如果排序之后产生了新的区间 就将区间的两个端点再次进行入栈操作 。一直到区间只有一个元素或者为空就不用进行入栈操作 了。当整个栈为空时，那么就证明没有区间需要进行排序，那么此时排序就结束了！

重要思想：将原本的一次递归转换为了一次元素出栈和入栈操作

Ⅱ，代码实现

此时我们就需要将之前我们所学到的有关栈的数据操 作代码带入到这个排序函数中，而所使用到的关于栈的函数如下：

cpp 复制代码

typedef int STDataType;
//创建栈结构体
typedef struct Stack
{
	STDataType* a; 
	int top;
	int capacity;
}ST;
// 初始化栈 
void StackInit(ST* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->capacity = ps->top = 0;//top指向栈顶数据的下一位
}
// 入栈 
void StackPush(ST* ps, STDataType data)
{
	assert(ps);
	//判断空间是否足够
	if (ps->top == ps->capacity)
	{
		int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDataType* tmp = (STDataType*)realloc(ps->a,sizeof(STDataType) * newcapacity);
		if (tmp==NULL)
		{
			perror("realloc fail!");
			return;
		}
		ps->a = tmp;
		ps->capacity = newcapacity;
	}
	ps->a[ps->top] = data;
	ps->top++;
}
// 出栈 
void StackPop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	ps->top--;
}
// 获取栈顶元素 
STDataType StackTop(ST* ps)
{
	assert(ps);//栈不为空指针
	assert(ps->top > 0);//栈的数据个数不能为零
	STDataType tmp = ps->a[ps->top - 1];//top-1才为栈顶元素的下标
	return tmp;
}
// 检测栈是否为空
bool StackEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0;//若top为零，则为true;反之则为false
}
// 销毁栈 
void StackDestroy(ST* ps)
{
	free(ps->a);//释放动态数组空间
	ps->a = NULL;//防止野指针的出现
	ps->capacity = ps->top = 0;
}

有了栈操作函数 的支持，我们就可以开始**快速排序（非递归）**代码的实现了！代码如下:

cpp 复制代码

//快速排序的非递归实现
void QuickSortNonR(int* a, int left, int right)
{
	//创建一个栈
	ST s1;
	StackInit(&s1);
	//首先第一次向栈中插入需排序的区间两端点（先插右端点再插左端点）
	StackPush(&s1, right);
	StackPush(&s1, left);
	while (!StackEmpty(&s1))
	{
		//一次性取出栈中的两个元素作为所需要排序的区间的两个端点
		int begin = StackTop(&s1);
		StackPop(&s1);
		int end = StackTop(&s1);
		StackPop(&s1);
		int key = partsort1(a, begin, end);			
		//判断区间是否只有一个元素或者为空，若不是，则还没排序完，进行入栈操作
		if (key + 1 < end)
		{
			StackPush(&s1, end);
			StackPush(&s1, key + 1);
		}
		if (begin < key - 1)
		{
			StackPush(&s1, key - 1);
			StackPush(&s1, begin);
		}
	}
	//销毁掉栈
	StackDestroy(&s1);
}

五，归并排序

那么我们现在进入归并排序的学习，当然，归并排序 在排序中也是属于大哥量级的排序方式了。

递归实现：

1，思路讲解

假如我们现在有一对如下图的半有序序列 ，从中间分割得到的左右两个序列分别为有序序列：

那么我们可以使用如下的归并思想将该序列排为有序序列：

我们只需要创建一个新数组tmp，然后定义两个指针begin1和begin2，分别指向左右两个有序序列的头 ，比较两指针所指向的值，较小值则尾插在tmp数组中 并且该指针进行自加操作。 当其中一个序列指针走完了 ，另一个还没有 时，就将不为空的序列全部尾插进tmp当中。

那么依照此方法，我们就可以得到一个有序的tmp数组 ，最后我们只需要将tmp数组 里的值使用memcpy函数移动到原数组里边即可。

Ⅰ，提出问题

那么我们可能就会提出一个问题了，当我们被给到一个无序序列 ，又怎么会怎么巧，这个序列经过分割之后就形成了左右两个有序序列 呢？既然这样的概率很小，那我们又怎么能使用归并来解决问题呢？

Ⅱ，给出解法

其实问题的答案很简单，假如我们遇到如下图的情况：

那此时我们就可以交出我们的老朋友------递归来解决问题了。我们将这个无序序列 进行不断地进行左右分割 ，直到分割出的序列只有一个元素或者不存在 时，那么此时这个序列不就有序了吗？然后递归结束开始返回 ，不就可以使用我们的归并思想进行排序了吗？所以这个问题就被完美的解决了，如下图所示：

2，代码实现

有了前面的思路讲解，我们就可以靠代码实现归并排序了。但要注意的是，因为tmp数组我们只需要一个，所以我们应当在归并排序函数的子函数 中进行递归操作 ，不然不停的递归就会不停地创建tmp数组 ，会造成空间的极大浪费！

那么我们的归并排序代码如下：

cpp 复制代码

//归并排序子函数
void _MergeSort(int* a, int* tmp, int begin, int end)
{
	//当序列只有一个元素或者为空时就返回
	if (begin >= end)
	{
		return;
	}
	//使用mid进行序列分割
	int mid = (begin + end) / 2;
	//首先使用递归的思想将序列排为有序
	//将区间分为[begin,mid]和[mid+1,end],使左右两区间分别有序之后再归并排序
	_MergeSort(a, tmp, begin, mid);
	_MergeSort(a, tmp, mid + 1, end);
	//begin1和end1来遍历左有序区间
	int begin1 = begin;
	int end1 = mid;
	//begin2和end2来遍历右有序区间
	int begin2 = mid + 1;
	int end2 = end;
	int i = begin;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}
	//将剩下的非空序列全部尾插进tmp中
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}
	//最后将tmp数组里的值使用memcpy函数移动到原数组里边即可
	memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
//归并排序
void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail!");
		return;
	}
	_MergeSort(a, tmp, 0, n - 1);
	free(tmp);
	tmp = NULL;
}

非递归实现：

1，思路讲解

这次我们将要学习到的归并排序的非递归方法算得上一个较难的知识点了，而这次我们并没有选择用桟来解决问题，而是选择使用循环。现在我们以如下图的例子来进行讲解：

那么对于这个无序序列，我们可以定义一个整型变量gap 来代表每组归并的数据个数，如下图所示：

那么这样，我们按照如下代码使用循环依次使用gap为begin1和end1，begin2和end2赋值 ，那么不就可以完成对整个序列的归并排序了吗？

cpp 复制代码

int gap = 1;
for (int i = 0; i < n; i += 2 * gap)
{
	int begin1 = i, end1 = i + gap - 1;
	int begin2 = i + gap, end2 = i + 2 * gap - 1;
    //对每两组进行归并排序
    //......
}
gap *= 2;

Ⅰ，提出问题

现在让我们仔细思考一下以上的代码是否还具有缺陷 ，其实答案很明显，该段代码确实可以解决一部分的归并排序的区间分配问题 ，但是当我们的无序序列 的长度不为2的次方倍 的时候，那么以上使用gap对区间变量begin1和end1，begin2和end2 进行赋值的方法就会存在数组越界的问题。

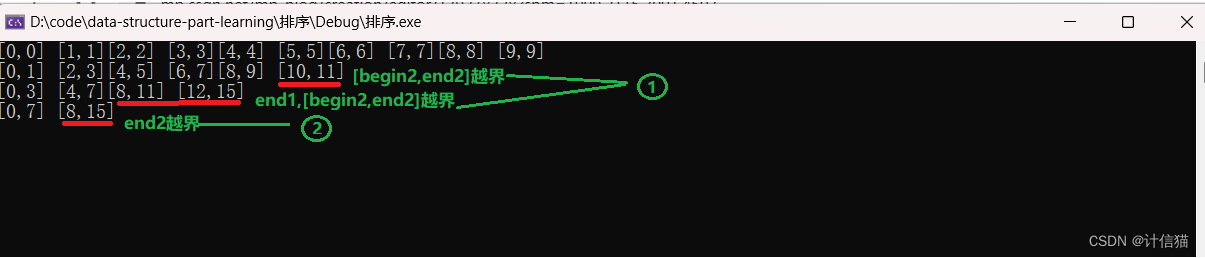
例如当我们的无序序列长度为10的时候，那么区间的范围应该在0~9之间，但当我们运行代码 并且打印归并区间时就会出现如下情况：

所以我们可以很明显地发现，如图标红的区间是存在越界访问的情况：

Ⅱ，给出解法

那么此时为了避免越界访问的问题 ，我们就可以将越界访问问问题分为如下两组：

当组①的情况出现时，其实我们就可以直接跳过此次归并；当组②的情况出现时，我们就可以将end2 进行调整为n-1就可以了。

2，代码实现

那么有了前面的理论支持下，我们就可以轻松地写出归并排序的非递归实现代码了！

cpp 复制代码

//归并排序------非递归
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail!");
		return;
	}
	//给gap初始值为1
	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			int j = i;
			//调整部分，防止数组越界访问
			if ( begin2 > n - 1)
			{
				break;
			}
			if (end2 > n - 1)
			{
				end2 = n - 1;
			}
			//开始归并排序
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}
			//将剩下的非空序列全部尾插进tmp中
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
			//拷贝数组数据
			memcpy(a + i, tmp + i, (end2 - i + 1) * sizeof(int));
		}
		//调整gap值
		gap *= 2;
	}
	//malloc之后勿忘释放内存空间并防止野指针的出现
	free(tmp);
	tmp = NULL;
}

六，结语

本篇博客所讲到的知识是我在数据结构学习中的最后一环 ，当然，也几乎是最重要的一环。当我于此刻将几种排序代码的准确无误、简单明了地表达在博客上时，那也证明我成功的掌握了这些知识，当然，同时也希望有着代码学习意向的你能将本篇博客的内容搞懂，手撕这些代码，这将对我们的代码能力有极大的提升！！

进入暑假，我也将进入C++**计算机语言 的学习，到时候我也会跟随学习进度更新相应的博客** 内容，如果你也有学习**C++**的倾向，那不妨点个关注，你的支持就是我最大的更新动力！！