迪杰斯特拉算法——C语言

迪杰斯特拉算法是一种用于在图中寻找节点之间最短路径的算法。它常用于路由以及其他图算法的子过程。

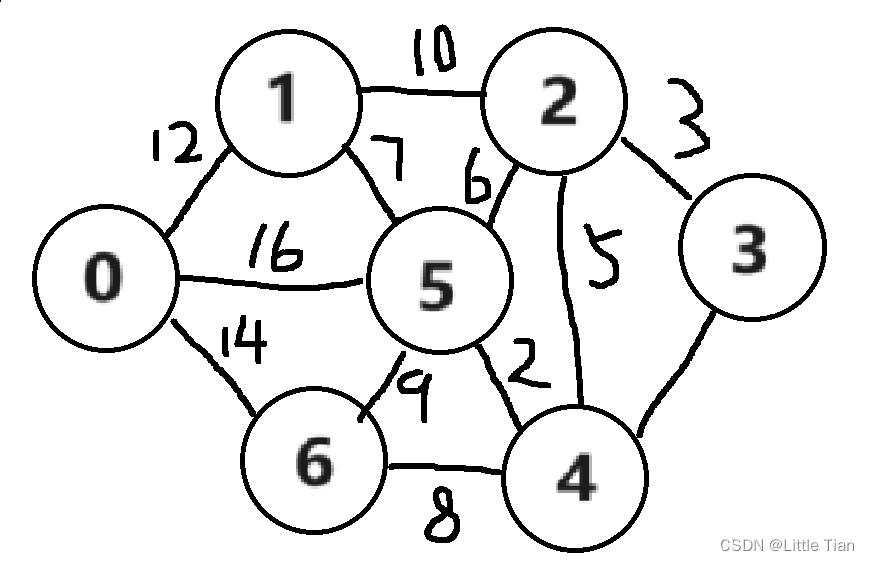
假设我们输入的是0顶点：

第一步，先寻找距离最小的顶点，这也是我们找到的第一个顶点，也就是顶点1，因为其他顶点距离一定大于12（未连接的顶点一定大于12，因为需要中转）。

第二步，把最近顶点作为中转点（顶点1）标记已访问，遍历其他未访问顶点，更新到顶点0 的距离（将顶点1作为中转点更新距离）。

第三步，重复第一步和第二步。

我们可以写出类似于这样的代码：

cpp 复制代码

void Dijkstra(Graph* G,int index) {
    开辟访问未访问数组
    开辟距离顶点index距离数组
	for (int i = 0; i < G->vexsNum; i++) {
        初始化两个数组

	}
	for (int a = 0; a < G->vexsNum - 1; a++) {
        找到最小距离的顶点
        标记已访问
        for (int j = 0; j < G->vexsNum; j++) {
	    if (未访问 && 经过中转点的距离 < 距离数组的距离) {
            更新距离
	    }
        }
	}


}

寻找最小距离顶点的代码如下：

cpp 复制代码

int GetMin(Graph* G,int* S,int* D) {
	int min = Max;
	int index;
	for (int i = 0; i < G->vexsNum;i++) {
		if (S[i] == 0 && D[i] > 0) {
			if (min > D[i]) {
				min = D[i];
				index = i;
			}
		}
	}
	return index;
}

接下来是迪杰斯特拉算法的代码：

cpp 复制代码

void Dijkstra(Graph* G,int index) {
	int* S = (int*)malloc(sizeof(int) * G->vexsNum);
	int* D = (int*)malloc(sizeof(int) * G->vexsNum);
	for (int i = 0; i < G->vexsNum; i++) {
		if (i == index) {
			S[i] = 1;
		}
		else
		{
			S[i] = 0;
		}
		D[i] = G->arcs[index][i];
	}
	for (int a = 0; a < G->vexsNum - 1; a++) {
		index = GetMin(G, S, D);
		S[index] = 1;
		for (int j = 0; j < G->vexsNum; j++) {
			if (S[index] != 0 && D[index] + G->arcs[index][j] < D[j]) {
				D[j] = D[index] + G->arcs[index][j];
			}
		}
	}

}

初始化将输入顶点标记为1，未访问顶点标记为0。

我们可以模拟顶点1为中转点的情况，这时连接顶点2 的距离就由Max变为12+10=22。其他结果都不变。

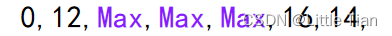
然后接着寻找最小顶点顶点6（顶点1已经访问过了），这时顶点6 作为中转点，连接顶点4 的距离就由Max变为14+8=22。其他结果不变。

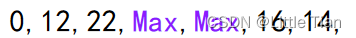
现在接着寻找最小顶点顶点5，依次类推。

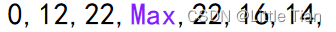
最后结果如下：

这就是文章的全部内容了，希望对你有所帮助，如有错误欢迎指出。