统计学是数据科学项目的重要组成部分。每当我们想从数据集的样本中对数据集的总体进行任何推断,从数据集中收集信息,或者对数据集的参数进行任何假设时,我们都会使用统计工具。
中心极限定理
定义:中心极限定理,通俗地来说,就是研究独立随机变量和的极限分布为正态分布的问题。在自然界和生产中,许多现象受到许多相互独立的随机因素的影响。当每个因素的影响都很微小时,这些因素产生的总影响可以看作是服从正态分布的。中心极限定理就是从数学上证明了这一现象。
具体来说,中心极限定理表明,无论随机变量的初始分布是什么,只要我们对这些随机变量进行大量的独立抽取,并将这些随机变量加起来,那么这些总和的分布就会接近正态分布。这种规律在我们的生活中也随处可见,比如人的身高、体重等数据的分布都近似于正态分布。
举个例子:
假设有一个班级,其中学生的成绩是随机变量,每个学生都是一个独立的随机变量。如果我们把所有学生的成绩加起来,并计算平均分,那么这个平均分的分布就会接近正态分布。
具体来说,我们可以将每个学生的成绩看作是一个独立的随机变量,每个随机变量都有自己的分布。如果我们把所有学生的成绩加起来,那么这个总和就是一个随机变量。根据中心极限定理,这个总和的分布就会接近正态分布。
这个例子可以用来解释为什么大多数情况下,班级的平均分分布会呈现出一个类似于正态分布的形状。这是因为每个学生的成绩都是独立的随机变量,而这些随机变量的总和近似于正态分布。
应用场景
中心极限定理在数理统计和概率论中有着广泛的应用,主要包括以下几个方面:
- 验证数据是否满足正态分布:如果数据符合正态分布的条件,则可以使用相关的统计方法进行分析。而如果数据不符合正态分布的条件,就需要采用其他的统计方法进行分析。
- 求解总体参数:中心极限定理可以用于求解总体的均值和方差等参数。通过对样本进行一些简单的统计分析,就可以根据中心极限定理的推导,得到总体的均值和方差等参数的近似值。
- 构造置信区间:当对总体参数进行估计时,可以使用中心极限定理的知识,构造置信区间进行区间估计,从而提高估计的可靠性。
- 应用于大样本:在处理大样本时,中心极限定理是非常重要的工具。它能够证明在样本容量足够大的情况下,样本均值的分布近似于正态分布,从而可以应用正态分布的统计性质进行各种统计推断。
- 解决实际问题:中心极限定理可以用于解决许多实际问题,例如金融领域中的风险评估、医学领域中的临床试验、生产制造中的质量控制等。在这些领域中,中心极限定理可以帮助我们理解数据的分布规律,并进行更准确的预测和决策。
总之,中心极限定理是概率论中的一组非常重要的定理,它揭示了大量随机变量之和的分布规律,并广泛应用于数理统计学、误差分析、自然与生产现象的解释等领域。在实际应用中,它可以用于验证数据的分布、求解总体参数、构造置信区间、应用于大样本以及解决各种实际问题。
中心极限定理的Python实现
python
import numpy
import matplotlib.pyplot as plt
# number of sample
num = [1, 10, 50, 100]
# list of sample means
means = []
# Generating 1, 10, 30, 100 random numbers from -40 to 40
# taking their mean and appending it to list means.
for j in num:
# Generating seed so that we can get same result
# every time the loop is run...
numpy.random.seed(1)
x = [numpy.mean(
numpy.random.randint(
-40, 40, j)) for _i in range(1000)]
means.append(x)
k = 0
# plotting all the means in one figure
fig, ax = plt.subplots(2, 2, figsize =(8, 8))
for i in range(0, 2):
for j in range(0, 2):
# Histogram for each x stored in means
ax[i, j].hist(means[k], 10, density = True)
ax[i, j].set_title(label = num[k])
k = k + 1
plt.show()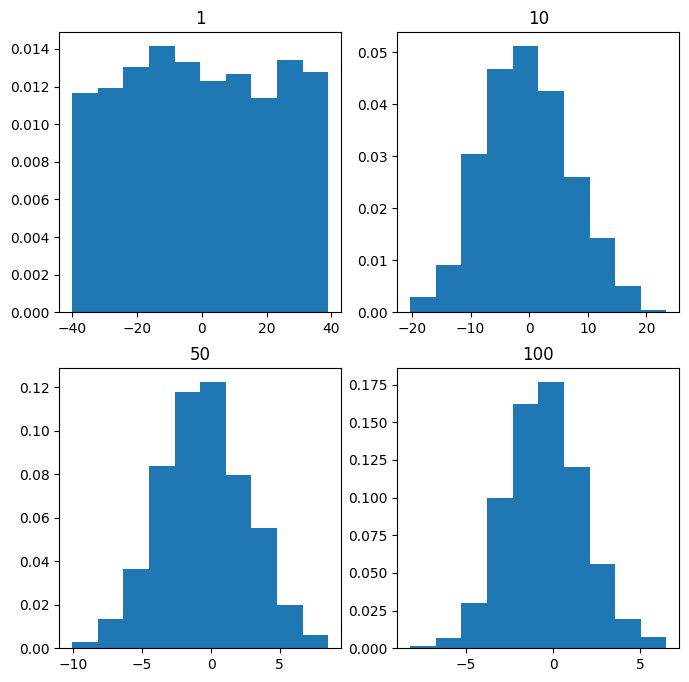
从图中可以明显看出,随着样本量从1增加到100,直方图趋于正态分布。
中心极限定理的经验法则
中心极限定理的经验法则是指在实际应用中,如果随机变量足够多,那么这些随机变量之和的分布近似于正态分布。这个经验法则在数理统计学和误差分析中非常重要,可以用来解决各种实际问题。
例如,在金融领域中,中心极限定理的经验法则可以用来评估投资组合的风险。通过将大量的股票价格看作是随机变量,并计算它们的均值和方差,就可以得到投资组合的收益率分布。由于这些随机变量足够多,它们的分布近似于正态分布,因此可以使用正态分布的性质来计算投资组合的风险。
在生产制造中,中心极限定理的经验法则可以用来控制产品质量。通过对生产过程中产生的大量数据进行分析,可以计算出这些数据的均值和方差,并根据中心极限定理的推导,得到这些数据的分布近似于正态分布。因此,可以根据正态分布的性质制定控制限,控制产品质量,提高生产效率。
总之,中心极限定理的经验法则是数理统计学和误差分析中非常重要的一个工具,可以用来解决各种实际问题。在实际应用中,只要随机变量足够多,它们的分布就可以近似地看作是正态分布,从而可以使用正态分布的性质进行各种统计推断。