文章目录
- 1.Eigne库介绍
- 2.Eigne库安装
- 3.Eigne库使用
- [4.some examples](#4.some examples)
- 5.参考文献
1.Eigne库介绍
Eigen是可以用来进行线性代数 、矩阵 、向量操作 等运算的C++库,它里面包含了很多算法。它的License是MPL2。它支持多平台。
Eigen采用源码的方式提供给用户使用,在使用时只需要包含Eigen的头文件即可进行使用。之所以采用这种方式,是因为Eigen采用模板方式实现,由于模板函数不支持分离编译,所以只能提供源码而不是动态库的方式供用户使用。
矩阵的定义 :Eigen中关于矩阵类的模板函数中,共有六个模板参数,常用的只有前三个。其前三个参数分别表示矩阵元素的类型、行数和列数 。矩阵定义时可以使用Dynamic来表示矩阵的行列数为未知。Eigen中无论是矩阵还是数组、向量,无论是静态矩阵还是动态矩阵都提供默认构造函数,也就是定义这些数据结构时都可以不用提供任何参数,其大小均由运行时来确定。矩阵的构造函数中只提供行列数、元素类型的构造参数,而不提供元素值的构造,对于比较小的、固定长度的向量提供初始化元素的定义。
矩阵类型:Eigen中的矩阵类型一般都是用类似MatrixXXX来表示,可以根据该名字来判断其数据类型,比如"d"表示double类型,"f"表示float类型,"i"表示整数,"c"表示复数;Matrix2f,表示的是一个2*2维的,其每个元素都是float类型。
数据存储:Matrix创建的矩阵默认是按列存储,Eigen在处理按列存储的矩阵时会更加高效。如果想修改可以在创建矩阵的时候加入参数,如:
Matrix<int,3, 4, ColMajor> Acolmajor;
Matrix<int,3, 4, RowMajor> Arowmajor;动态矩阵和静态矩阵:动态矩阵是指其大小在运行时确定,静态矩阵是指其大小在编译时确定。
- MatrixXd:表示任意大小的元素类型为double的矩阵变量,其大小只有在运行时被赋值之后才能知道。
- Matrix3d:表示元素类型为double大小为3*3的矩阵变量,其大小在编译时就知道。
在Eigen中行优先的矩阵会在其名字中包含有row,否则就是列优先。
Eigen中的向量只是一个特殊的矩阵,其维度为1而已。
矩阵元素的访问 :在矩阵的访问中,行索引总是作为第一个参数,Eigen中矩阵、数组、向量的下标都是从0开始。矩阵元素的访问可以通过"()"操作符完成。例如m(2, 3)既是获取矩阵m的第2行第3列元素。针对向量还提供"[]"操作符,注意矩阵则不可如此使用。
设置矩阵的元素:在Eigen中重载了"<<"操作符,通过该操作符即可以一个一个元素的进行赋值,也可以一块一块的赋值。另外也可以使用下标进行赋值。
重置矩阵大小:当前矩阵的行数、列数、大小可以通过rows()、cols()和size()来获取,对于动态矩阵可以通过resize()函数来动态修改矩阵的大小。注意:(1)、固定大小的矩阵是不能使用resize()来修改矩阵的大小;(2)、resize()函数会析构掉原来的数据,因此调用resize()函数之后将不能保证元素的值不改变;(3)、使用"="操作符操作动态矩阵时,如果左右两边的矩阵大小不等,则左边的动态矩阵的大小会被修改为右边的大小。
如何选择动态矩阵和静态矩阵?
Eigen对于这问题的答案是:对于小矩阵(一般大小小于16)的使用固定大小的静态矩阵,它可以带来比较高的效率,对于大矩阵(一般大小大于32)建议使用动态矩阵。还需特别注意的是:如果特别大的矩阵使用了固定大小的静态矩阵则可能造成栈溢出的问题。
2.Eigne库安装
首先,在官网 Eigen上下载源码安装包

然后,编译源码:
bash
进入源码目录
mkdir build
cd build
cmake ..
sudo make install
#安装后,头文件安装在/usr/local/include/eigen3/Eigen
#移动头文件
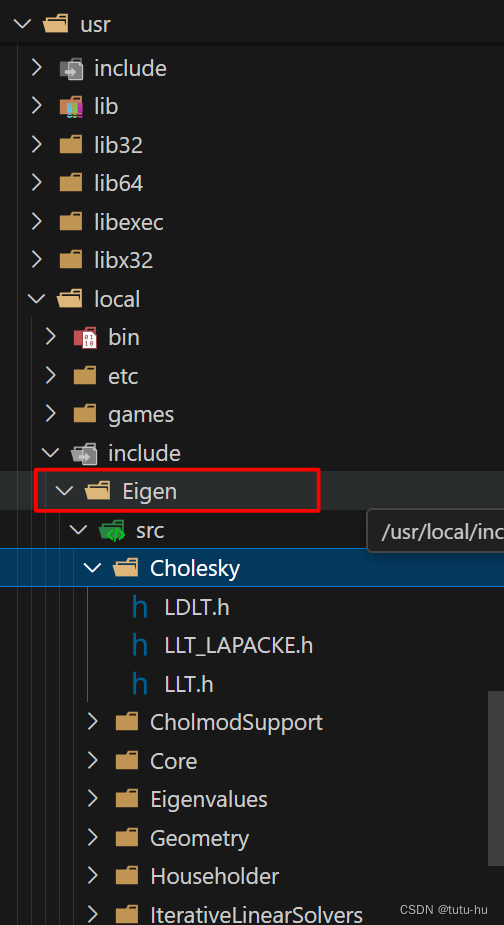
sudo cp -r /usr/local/include/eigen3/Eigen /usr/local/include备注:因为eigen3 被默认安装到了usr/local/include里了(或者是usr/include里,这两个都差不多,都是系统默认的路径),在很多程序中include时经常使用#include <Eigen/Dense>而不是使用#include <eigen3/Eigen/Dense>所以要做下处理,否则一些程序在编译时会因找不到Eigen/Dense而报错。上面指令将usr/local/include/eigen3文件夹中的Eigen文件递归地复制到上一层文件夹(直接放到/usr/local/include中,否则系统无法默认搜索到 -> 此时只能在CMakeLists.txt用include_libraries(绝对路径了))。只有头文件就够用了,没有.so库文件!
3.Eigne库使用
- 创建一个
eginetest.cpp源文件如下,包含<Eigen/Dense>头文件:
bash
#include <iostream>
#include <Eigen/Dense>
template <typename T>
static void matrix_mul_matrix(T* p1, int iRow1, int iCol1, T* p2, int iRow2, int iCol2, T* p3)
{
if (iRow1 != iRow2) return;
//列优先
//Eigen::Map< Eigen::Matrix<T, Eigen::Dynamic, Eigen::Dynamic> > map1(p1, iRow1, iCol1);
//Eigen::Map< Eigen::Matrix<T, Eigen::Dynamic, Eigen::Dynamic> > map2(p2, iRow2, iCol2);
//Eigen::Map< Eigen::Matrix<T, Eigen::Dynamic, Eigen::Dynamic> > map3(p3, iCol1, iCol2);
//行优先
Eigen::Map< Eigen::Matrix<T, Eigen::Dynamic, Eigen::Dynamic, Eigen::RowMajor> > map1(p1, iRow1, iCol1);
Eigen::Map< Eigen::Matrix<T, Eigen::Dynamic, Eigen::Dynamic, Eigen::RowMajor> > map2(p2, iRow2, iCol2);
Eigen::Map< Eigen::Matrix<T, Eigen::Dynamic, Eigen::Dynamic, Eigen::RowMajor> > map3(p3, iCol1, iCol2);
map3 = map1 * map2;
}
int main(int argc, char* argv[])
{
//1. 矩阵的定义
Eigen::MatrixXd m(2, 2);
Eigen::Vector3d vec3d;
Eigen::Vector4d vec4d(1.0, 2.0, 3.0, 4.0);
//2. 动态矩阵、静态矩阵
Eigen::MatrixXd matrixXd;
Eigen::Matrix3d matrix3d;
//3. 矩阵元素的访问
m(0, 0) = 1;
m(0, 1) = 2;
m(1, 0) = m(0, 0) + 3;
m(1, 1) = m(0, 0) * m(0, 1);
std::cout << m << std::endl << std::endl;
//4. 设置矩阵的元素
m << -1.5, 2.4,
6.7, 2.0;
std::cout << m << std::endl << std::endl;
int row = 4;
int col = 5;
Eigen::MatrixXf matrixXf(row, col);
matrixXf << 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20;
std::cout << matrixXf << std::endl << std::endl;
matrixXf << Eigen::MatrixXf::Identity(row, col);
std::cout << matrixXf << std::endl << std::endl;
//5. 重置矩阵大小
Eigen::MatrixXd matrixXd1(3, 3);
m = matrixXd1;
std::cout << m.rows() << " " << m.cols() << std::endl << std::endl;
//6. 矩阵运算
m << 1, 2, 7,
3, 4, 8,
5, 6, 9;
std::cout << m << std::endl;
matrixXd1 = Eigen::Matrix3d::Random();
m += matrixXd1;
std::cout << m << std::endl << std::endl;
m *= 2;
std::cout << m << std::endl << std::endl;
std::cout << -m << std::endl << std::endl;
std::cout << m << std::endl << std::endl;
//7. 求矩阵的转置、共轭矩阵、伴随矩阵
std::cout << m.transpose() << std::endl << std::endl;
std::cout << m.conjugate() << std::endl << std::endl;
std::cout << m.adjoint() << std::endl << std::endl;
std::cout << m << std::endl << std::endl;
m.transposeInPlace();
std::cout << m << std::endl << std::endl;
//8. 矩阵相乘、矩阵向量相乘
std::cout << m*m << std::endl << std::endl;
vec3d = Eigen::Vector3d(1, 2, 3);
std::cout << m * vec3d << std::endl << std::endl;
std::cout << vec3d.transpose()*m << std::endl << std::endl;
//9. 矩阵的块操作
std::cout << m << std::endl << std::endl;
std::cout << m.block(1, 1, 2, 2) << std::endl << std::endl;
std::cout << m.block<1, 2>(0, 0) << std::endl << std::endl;
std::cout << m.col(1) << std::endl << std::endl;
std::cout << m.row(0) << std::endl << std::endl;
//10. 向量的块操作
Eigen::ArrayXf arrayXf(10);
arrayXf << 1, 2, 3, 4, 5, 6, 7, 8, 9, 10;
std::cout << vec3d << std::endl << std::endl;
std::cout << arrayXf << std::endl << std::endl;
std::cout << arrayXf.head(5) << std::endl << std::endl;
std::cout << arrayXf.tail(4) * 2 << std::endl << std::endl;
//11. 求解矩阵的特征值和特征向量
Eigen::Matrix2f matrix2f;
matrix2f << 1, 2, 3, 4;
Eigen::SelfAdjointEigenSolver<Eigen::Matrix2f> eigenSolver(matrix2f);
if (eigenSolver.info() == Eigen::Success) {
std::cout << eigenSolver.eigenvalues() << std::endl << std::endl;
std::cout << eigenSolver.eigenvectors() << std::endl << std::endl;
}
//12. 类Map及动态矩阵的使用
int array1[4] = { 1, 2, 3, 4 };
int array2[4] = { 5, 6, 7, 8 };
int array3[4] = { 0, 0, 0, 0};
matrix_mul_matrix(array1, 2, 2, array2, 2, 2, array3);
for (int i = 0; i < 4; i++)
std::cout << array3[i] << std::endl;
return 0;
}- 编译:
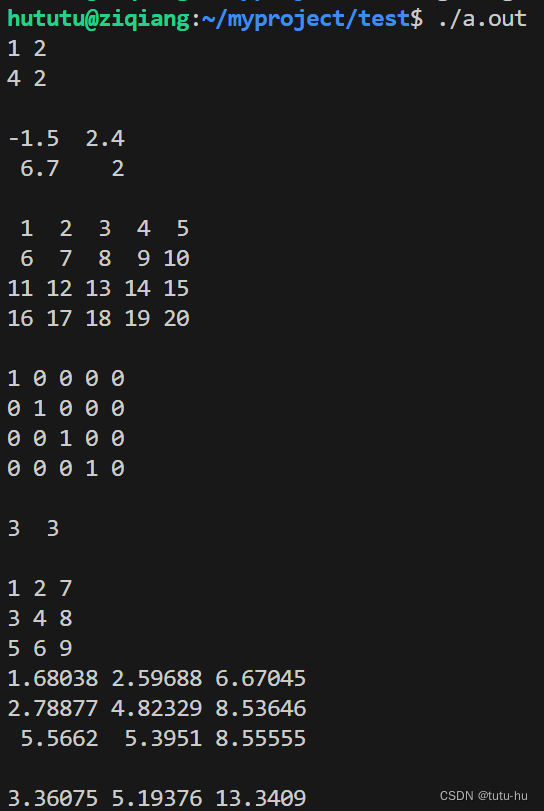
g++ eginetest.cpp - 运行:
./a.out - 输出结果如下: