GBDT算法详解

GBDT算法详解

梯度提升决策树（Gradient Boosting Decision Trees，GBDT）是机器学习中一种强大的集成算法。它通过构建一系列的决策树，并逐步优化模型的预测能力，在各种回归和分类任务中取得了显著的效果。本文将详细介绍GBDT算法的原理，并展示其在实际数据集上的应用。

GBDT算法原理

GBDT是一种集成学习方法，通过逐步建立多个决策树，每棵树都在前一棵树的基础上进行改进。GBDT的基本思想是逐步减少残差（即预测误差），使模型的预测能力不断提高。

算法步骤

1. 初始化模型：使用常数模型初始化，比如回归问题中可以用目标值的均值初始化模型。
2. 计算残差：计算当前模型的残差，即预测值与真实值之间的差异。
3. 拟合残差：用新的决策树拟合残差，并更新模型。
4. 更新模型：将新决策树的预测结果加到模型中，以减少残差。
5. 重复步骤2-4：直到达到预设的迭代次数或残差足够小。

公式表示

初始化模型：
F 0 ( x ) = arg ⁡ min ⁡ γ ∑ i = 1 n L ( y i , γ ) F_0(x) = \arg\min_{\gamma} \sum_{i=1}^{n} L(y_i, \gamma) F0(x)=argγmini=1∑nL(yi,γ)

对于每一次迭代 (m = 1, 2, \ldots, M)：

1. 计算负梯度（残差）： r i m = − [ ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ] F ( x ) = F m − 1 ( x ) r_{im} = -\left[ \frac{\partial L(y_i, F(x_i))}{\partial F(x_i)} \right]{F(x) = F{m-1}(x)} rim=−[∂F(xi)∂L(yi,F(xi))]F(x)=Fm−1(x)

2. 拟合一个新的决策树来预测残差： h m ( x ) = arg ⁡ min ⁡ h ∑ i = 1 n ( r i m − h ( x i ) ) 2 h_m(x) = \arg\min_{h} \sum_{i=1}^{n} (r_{im} - h(x_i))^2 hm(x)=arghmini=1∑n(rim−h(xi))2

3. 更新模型： F m ( x ) = F m − 1 ( x ) + ν h m ( x ) F_m(x) = F_{m-1}(x) + \nu h_m(x) Fm(x)=Fm−1(x)+νhm(x)

   其中， ν \nu ν是学习率，控制每棵树对最终模型的贡献。

GBDT算法的特点

1. 高准确性：GBDT通过逐步减少残差，不断优化模型，使其在很多任务中具有很高的准确性。
2. 灵活性：GBDT可以处理回归和分类任务，并且可以使用各种损失函数。
3. 鲁棒性：GBDT对数据的噪声和异常值有一定的鲁棒性。
4. 可解释性：决策树本身具有一定的可解释性，通过特征重要性等方法可以解释GBDT模型。

GBDT参数说明

以下是GBDT（Gradient Boosting Decision Trees，梯度提升决策树）常用参数及其详细说明：

参数名称	描述	默认值	示例
n_estimators	树的棵数，提升迭代的次数	100	n_estimators=200
learning_rate	学习率，控制每棵树对最终模型的贡献	0.1	learning_rate=0.05
max_depth	树的最大深度，控制每棵树的复杂度	3	max_depth=4
min_samples_split	分裂一个内部节点需要的最少样本数	2	min_samples_split=5
min_samples_leaf	叶子节点需要的最少样本数	1	min_samples_leaf=3
subsample	样本采样比例，用于训练每棵树	1.0	subsample=0.8
max_features	寻找最佳分割时考虑的最大特征数	None	max_features='sqrt'
loss	要优化的损失函数	deviance	loss='exponential'
criterion	分裂节点的标准	friedman_mse	criterion='mae'
init	初始估计器	None	init=some_estimator
random_state	随机数种子，用于结果复现	None	random_state=42
verbose	控制训练过程信息的输出频率	0	verbose=1
warm_start	是否使用上次调用的解决方案来初始化训练	False	warm_start=True
presort	是否预排序数据以加快分裂查找	deprecated	-
validation_fraction	用于提前停止训练的验证集比例	0.1	validation_fraction=0.2
n_iter_no_change	如果在若干次迭代内验证集上的损失没有改善，则提前停止训练	None	n_iter_no_change=10
tol	提前停止的阈值	1e-4	tol=1e-3
ccp_alpha	最小成本复杂度修剪参数	0.0	ccp_alpha=0.01

通过合理调整这些参数，可以优化GBDT模型在特定任务和数据集上的性能。

GBDT算法在回归问题中的应用

在本节中，我们将使用波士顿房价数据集来展示如何使用GBDT算法进行回归任务。

导入库

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import mean_squared_error, r2_score

加载和预处理数据

# 生成合成回归数据集
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=42)

# 数据集划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 数据标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

训练GBDT模型

# 训练GBDT模型
gbdt = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1, max_depth=3, random_state=42)
gbdt.fit(X_train, y_train)

预测与评估

# 预测
y_pred = gbdt.predict(X_test)

# 评估
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f'Mean Squared Error: {mse:.2f}')
print(f'R^2 Score: {r2:.2f}')

特征重要性

# 特征重要性
# 特征重要性
feature_importances = gbdt.feature_importances_
plt.barh(range(X.shape[1]), feature_importances, align='center')
plt.yticks(np.arange(X.shape[1]), [f'Feature {i}' for i in range(X.shape[1])])
plt.xlabel('Feature Importance')
plt.ylabel('Feature')
plt.title('Feature Importances in GBDT')
plt.show()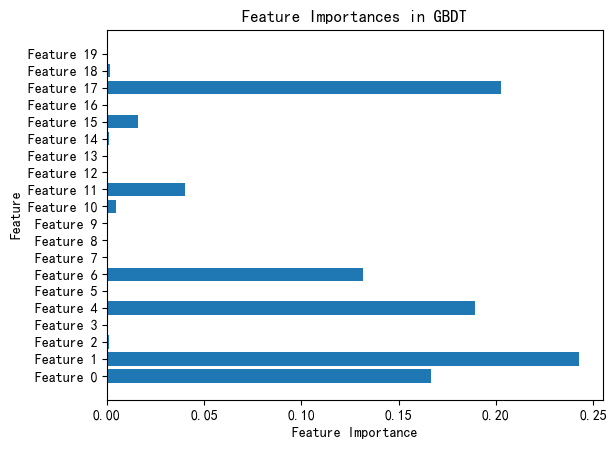

GBDT算法在分类问题中的应用

在本节中，我们将使用20类新闻组数据集来展示如何使用GBDT算法进行文本分类任务。

导入库

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report

加载和预处理数据

# 生成分类数据集
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=42)

# 数据集划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 数据标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

训练GBDT模型

# 训练GBDT模型
gbdt = GradientBoostingClassifier(n_estimators=100, learning_rate=0.1, max_depth=3, random_state=42)
gbdt.fit(X_train, y_train)

预测与评估

# 预测
y_pred = gbdt.predict(X_test)

# 评估
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.2f}')

# 混淆矩阵
conf_matrix = confusion_matrix(y_test, y_pred)
print('Confusion Matrix:')
print(conf_matrix)

# 分类报告
class_report = classification_report(y_test, y_pred)
print('Classification Report:')
print(class_report)

结语

本文详细介绍了GBDT算法的原理和特点，并展示了其在回归和分类任务中的应用。首先介绍了GBDT算法的基本思想和公式，然后展示了如何在回归数据集使用GBDT进行回归任务，以及如何在分类数据集上使用GBDT进行文本分类任务。