
总言
主要内容:编程题举例,熟悉理解记忆化搜索类题型(对比递归、动态规划理解运用)。
文章目录
- 总言
- 1、记忆化搜索
- 2、斐波那契数(easy)
- 3、不同路径(medium)
- 4、最长递增子序列(medium)
- 5、猜数字大小II(medium)
- 6、矩阵中的最长递增路径(hard)
- Fin、共勉。
1、记忆化搜索
1.1、基本介绍
1)、记忆搜索化是什么?主要用来解决什么问题的?
为了探究记忆搜索化的用途,我们以下述第一道题:斐波那契数为例,进行说明。
递归版的斐波那契数写法见下述:由递归展开图可知,假如我们要计算 d ( 5 ) d(5) d(5),则需要先计算 d ( 4 ) d(4) d(4) 和 d ( 3 ) d(3) d(3),而在计算 d ( 3 ) d(3) d(3) 时还需要计算 d ( 2 ) d(2) d(2) 和 d ( 1 ) d(1) d(1) 。这会带来一个问题: d ( 4 ) d(4) d(4) 、 d ( 3 ) d(3) d(3) 、 d ( 2 ) d(2) d(2) 、 d ( 1 ) d(1) d(1) 都进行了多次计算,即出现了大量重复计算的子问题。
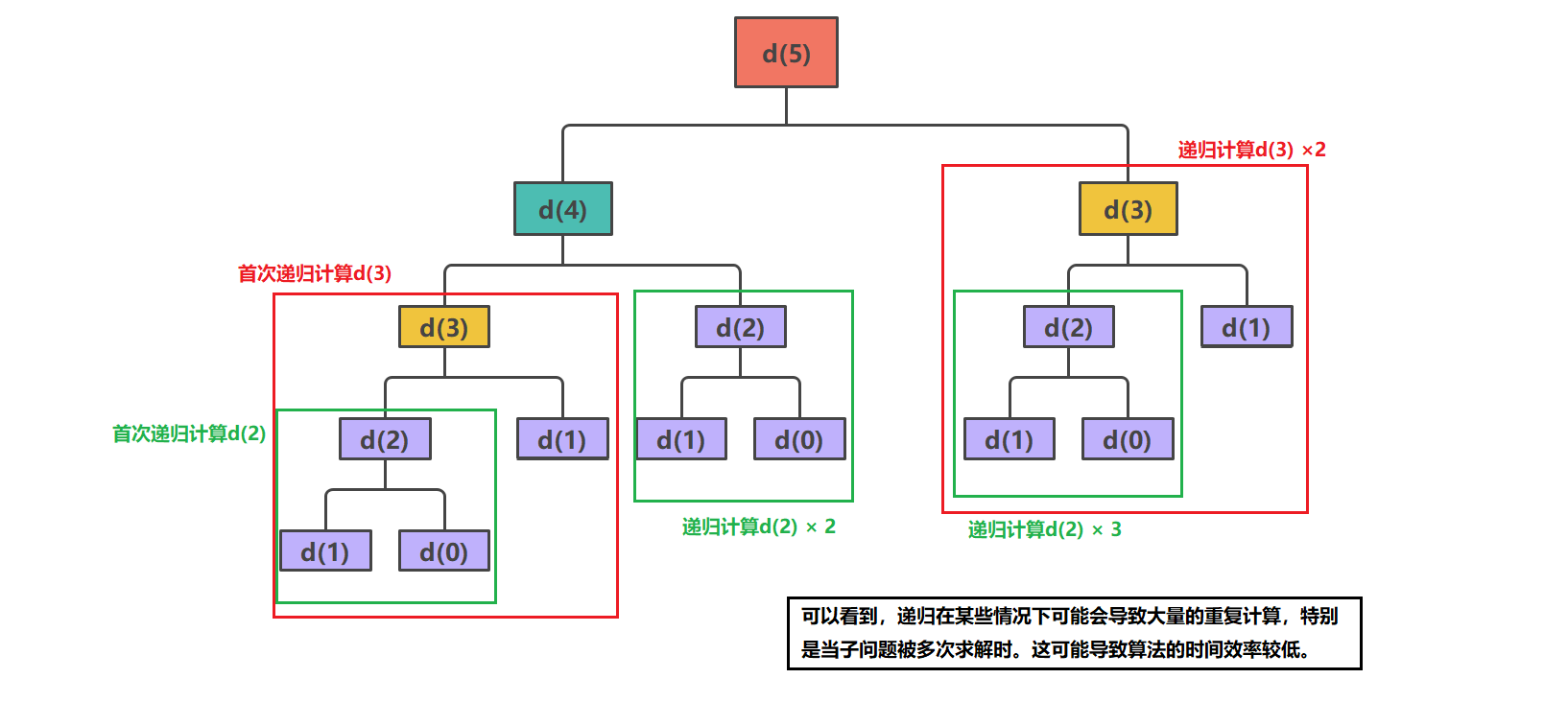
那么,有什么方法对其进行优化?
回答:为了避免此类重复计算,在递归时,我们可以使用一个备忘录(本质是一个数组或哈希表)来保存已经计算过的状态及其对应的结果。 这样,在后续递归过程中,每次调用可先检查一下所需的结果是否已经被计算并保存过? 若是,则直接从备忘录中返回所需结果;若否,则进行递归计算,同时将结果保存在备忘录中,以便后续使用。如此,就避免了重复计算问题。(也可以把它理解为一种剪枝操作)
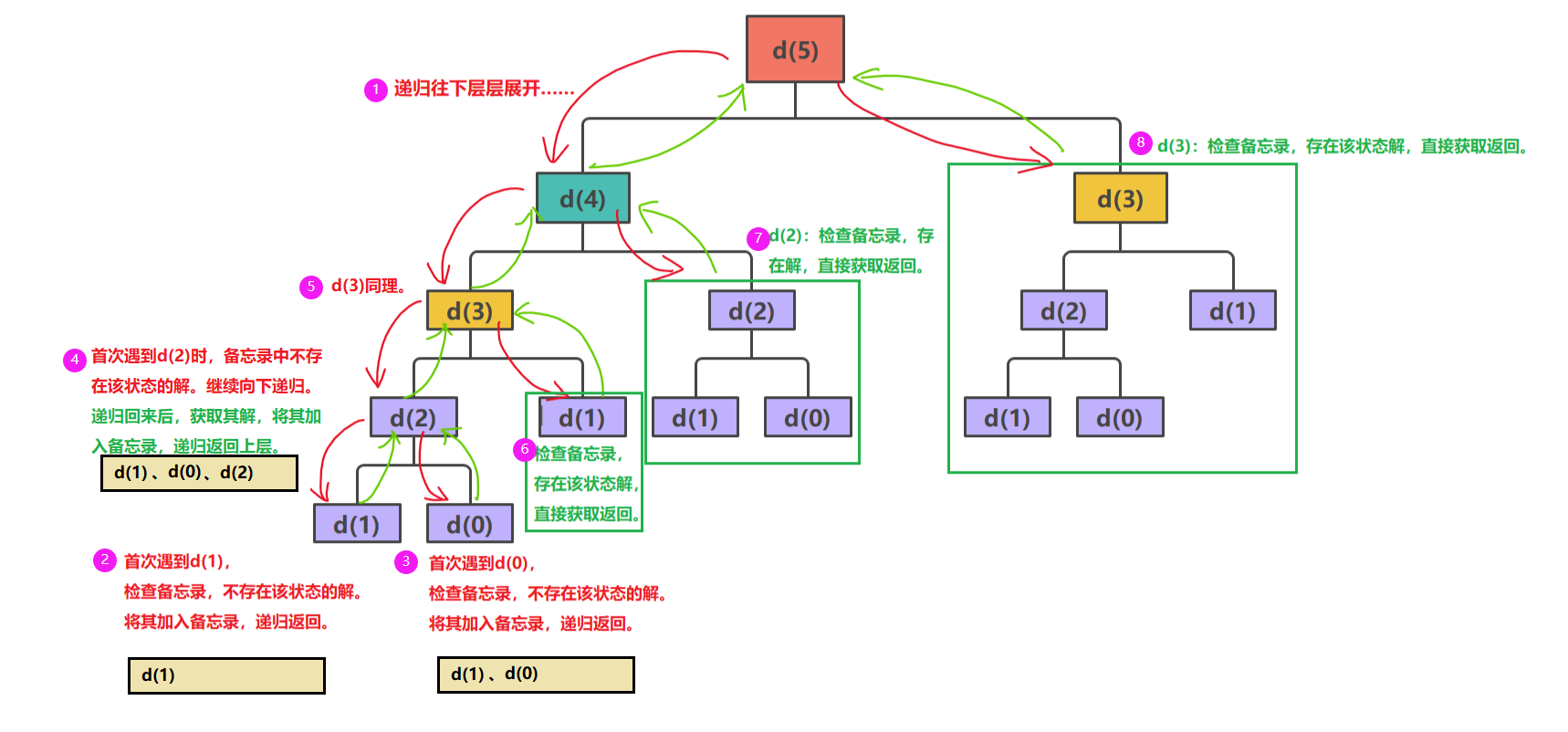
这也就是记忆搜索化 。一种结合了搜索和动态规划思想的算法策略。其核心思想是在搜索过程中,对于已经计算过的状态或子问题的解进行保存,当再次遇到相同的状态或子问题时,直接使用之前保存的结果,从而避免重复计算,提高算法效率。
2)、如何实现记忆搜索化?(一般性流程步骤 )
1、在常规的递归基础上,添加一个备忘录 (一个哈希表或数组,用于存储已经计算过的子问题的结果,以<参数,返回值>的键值对形式)
2、递归每次返回的时候,将结果放到备忘录里面。
3、在每次进入递归的时候,先检查备忘录里面是否存在所需计算结果。
1.2、细节理解(记忆搜索化、递归、动态规划......)
1)、 所有的递归(暴搜、 深搜) ,都能改成记忆化搜索吗?
回答:不是,只有在递归的过程中,出现了大量完全相同的问题时,才能用记忆化搜索的方式优化。
①记忆化搜索的优化效果主要体现在能够避免重复计算相同的子问题。 因此,只有当递归过程中存在大量重复的子问题,即 "子问题重叠"现象 时,采用记忆化搜索才是有意义的。
②如果递归算法中的子问题都是唯一的,或者重复的子问题数量很少 ,那么使用记忆化搜索可能并不会带来明显的性能提升,甚至可能由于记忆化存储结构的开销而降低效率。
2)、 动态规划 与 记忆化搜索
本质: ①均属于暴力解法(暴搜),②不过在其基础上进行了一定的优化(通过把已经计算过的值存起来的方式)。
实际上,《算法导论》中,将记忆化搜索与常规的动态规划都视为动态规划的一种形式,只是前者搜索时是以递归的方式进行的,而后者则是递推(循环)的方式。
实际写代码时,选哪种方式好?
在实际编写代码时,选择自顶向下(记忆化搜索)还是自底向上(动态规划)的方式取决于多个因素,包括问题的特性、代码的可读性、性能需求以及个人的编程习惯。
(暴搜→记忆化搜索→动态规划)在优化级别上,在很多情况下,将暴力搜索(暴搜)优化为记忆化搜索已经足够满足性能需求 ,而且这样的优化通常比完全重写为动态规划版本更加简单和直接。因此,在实际应用中,如果记忆化搜索已经足够好,那么可能没有必要再进一步将其改写为动态规划版本。
3)、 带备忘录的递归 vs 带备忘录的动态规划 vs 记忆化搜索
回答:根据2)可知,它们本质都是一回事。都利用了"记忆"或"存储"已经计算过的结果来避免重复计算,从而提高算法效率。只不过,它们在实现和应用上存在细节上的差别。
4)、 自顶向下和 vs 自低向上
自顶向下和自底向上的方法代表了两种不同的思考策略,它们的核心区别在于处理问题的顺序。
自顶向下(Top-Down) 方法通常从问题的最高层次(即整体或宏观层面)开始,逐步细化到更低层次的具体细节。这种方法的一个典型例子是递归算法和记忆化搜索。 在递归算法中,我们首先尝试解决整个问题,然后将其分解为更小的子问题。如果子问题已经被解决过(通过记忆化),则直接返回结果;否则,递归地解决子问题。这种方法的优势在于直观易理解,但如果不加记忆化,可能会导致大量的重复计算。
自底向上(Bottom-Up) 方法则相反,它从问题的最低层次(即微观层面)开始,逐步构建出更高层次的解决方案。动态规划是这种方法的典型代表。 在动态规划中,我们首先解决所有可能的子问题,并将它们的解存储在表格或数组中。然后,通过组合这些子问题的解来构建出原问题的解。这种方法避免了重复计算,但可能需要更多的存储空间来保存中间结果。
2、斐波那契数(easy)
题源:链接。

2.1、递归版
1)、一些说明
在上述我们介绍过记忆化搜索、递归相关理论部分的知识,这里是具体实现(动态规划相关专题会另写博文介绍,这里不做展开)。
下述版本重点在于理解递归版如何到记忆化搜索版,理解学习记忆化搜索的具体实现细节,对比递归版理解自顶向下和自底向上。
2)、题解
cpp
class Solution {
public:
int fib(int n) {
return DFS(n);
}
// 使用递归的方式
int DFS(int n)
{
if(n == 0 || n == 1)
return n;
return DFS(n-1) + DFS(n-2);
}
};2.2、记忆化搜索版
a、 加上⼀个备忘录;
b、 每次进⼊递归的时候,去备忘录里看看;
c、 每次返回的时候,将结果加入到备忘录中
cpp
class Solution {
// 使用一个备忘录:用于存储曾经获取的结果值
int memo[31];// 题目条件:0 <= n <= 30
public:
int fib(int n) {
memset(memo,-1,sizeof(memo));//void * memset ( void * ptr, int value, size_t num );
return DFS(n);
}
// 记忆化搜索版
int DFS(int n)
{
// 递归到当前层时:先查找备忘录,看该值是否已经计算过
if(memo[n] != -1) return memo[n];
// 来到此处,说明备忘录中没记录过该值,可以递归计算
if(n == 0 || n == 1)
{
memo[n] = n;// 递归返回前,先将数据记录入备忘录中
return n;
}
memo[n] = DFS(n-1) + DFS(n-2);// 递归返回前,先将数据记录入备忘录中
return memo[n];
}
};2.3、动态规划版
无非是将递归的那一套转换成了动态规划的那一套(这种先暴搜→再记忆化搜索→再改为动态规划的方式,不是任何动态规划都能用这个思路推导得出的。 )
a、递归含义 → 状态表示;
b、函数体 → 状态转移方程;
c、递归出口 → 初始化。
cpp
class Solution {
public:
// 动态规划版
int fib(int n) {
int dp[31];// 确定状态表示:dp[i]第i个斐波那契数
dp[0] = 0, dp[1] = 1;// 初始化状态
for(int i = 2; i <= n; ++i)
{
dp[i] = dp[i-1] + dp[i-2];//根据状态转移方程,填入数据
}
return dp[n];// 确定返回值。
}
};3、不同路径(medium)
题源:链接。

3.1、递归版(DFS)
1)、思路分析
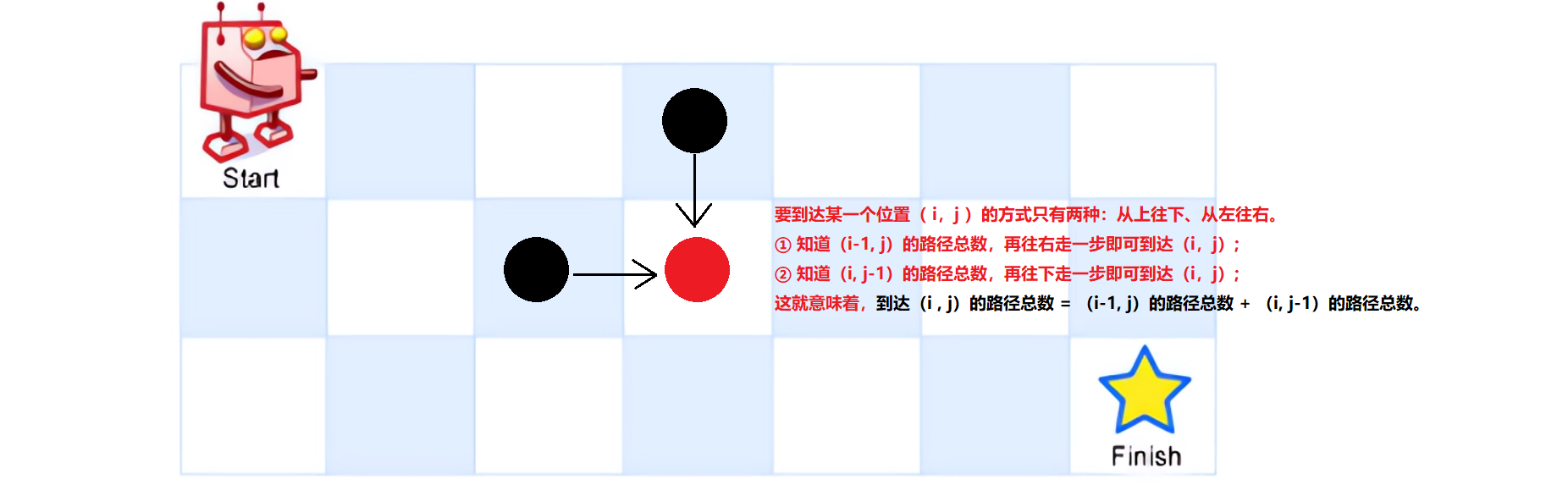
在普通递归版本中: 将要求位置传入递归函数中DFS(i,j),不管其过程如何,最终会为我们返回到达(i,j)位置的路径总数:有DFS(i,j) = DFS(i-1,j) + DFS(i, j-1)
2)、题解
简单的DFS、递归: 能解,但会超时。
这种是正着的写法,上述思路解析介绍的是倒着的写法。
cpp
class Solution {
int ret = 0;// 记录最终返回结果
int x;
int y;
public:
int uniquePaths(int m, int n) {
x = m -1, y = n-1;//下标实则为m-1,n-1
DFS(0,0);// 从(0,0)开始,向右或向下,走到(m-1,n-1)位置
return ret;
}
void DFS(int i, int j)
{
// 若当前i,j位置即终点位置,统计一次路径。
if(i == x && j == y)
{
++ret;
return;
}
// 向右遍历
if(j+1 <= y) DFS(i,j+1);
// 向下遍历
if(i+1 <= x) DFS(i+1,j);
}
};另一种写法:本质一样,只是这里是DFS采用了返回值的形式。
cpp
class Solution {
public:
int uniquePaths(int m, int n) {
return DFS(m-1,n-1);
}
int DFS(int i, int j)
{
if(i < 0 || j < 0) return 0;// 越界的情况
if(i == 0 && j == 0) return 1;// 此时在起点位置,路径只有一条
// 要计算当前能到达(i,j)位置的路径,只需要计算出能到达(i-1,j)和(i,j-1)两处的路径即可
return DFS(i-1,j) + DFS(i,j-1);
}
};3.2、记忆化搜索版
1)、分析
能否将上述暴搜改为记忆化搜索版本?关键在于递归过程中是否出现重复的子问题。
回答:可以改成记忆搜索化版本。这里在求终点的路径时,自顶向下递归调用过程中,会多次经过同一位置DFS(a,b)。因此,我们可以用一个备忘录将每次经过的DFS(a,b)存储,以便后续递归调用时直接返回。
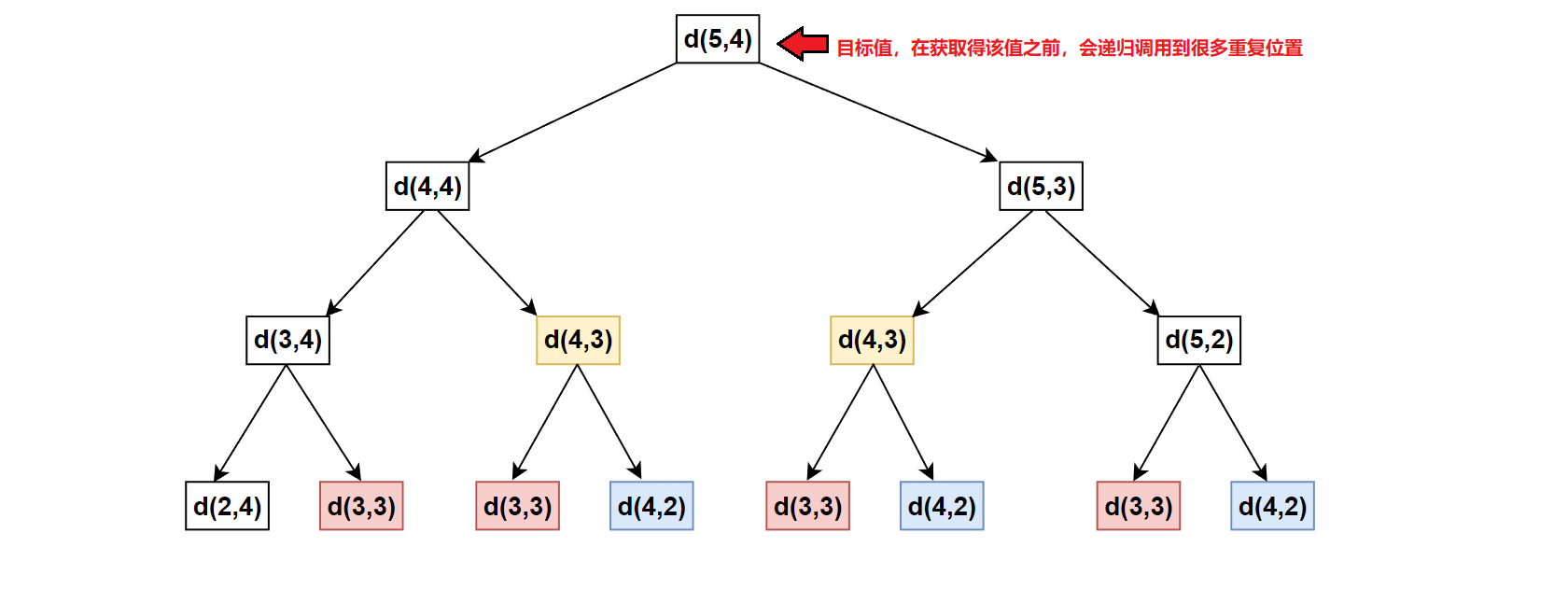
由于这里是二维数组(i,j),而备忘录以<可变参数,返回值>的键值对形式出现,这里的可变参数是元素下标位置。
2)、题解
这里,用于充当备忘录的二维数组memo可以写成类成员变量的形式,也可以写在函数中作为参数传递。
cpp
class Solution {
vector<vector<int>> memo;
public:
int uniquePaths(int m, int n) {
// 初始化
memo = vector<vector<int>>(m,vector<int>(n));// 这里我们从(0,0)作为原点计算。
memo[0][0] = 1;
return DFS(m-1,n-1);
}
int DFS(int i, int j)
{
// 越界处理
if(i < 0 || j < 0) return 0;
if(memo[i][j] != 0)// 记忆化搜索:先在备忘录中寻找当前值是否曾经计算过。
{
return memo[i][j];
}
// 要计算当前能到达(i,j)位置的路径,只需要计算出能到达(i-1,j)和(i,j-1)两处的路径即可
memo[i][j] = DFS(i,j-1) + DFS(i-1,j);// 记忆化搜索:返回前,先将值存入备忘录
return memo[i][j];
}
};3.3、动态规划版
状态表示:二维数组,dp[i][j],以(i,j)位置为结尾,表示到达(i,j)位置时的路径总数。
状态转移方程:dp[i][j] = dp[i-1][j] + dp[i][j-1]。
细节点:这里需要注意 i == 0 (首行)或者 j == 0 (首列)的时候,会发生越界行为。 根据题目描述可推测得,从(0,0)到这些位置无非只有一条路径可走(要么一直往右走、要么一直往下走),因此,对于这一行一列,可以单独拎出处理:dp[i][j] = 1。
cpp
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m, vector<int>(n));//m×n矩阵
dp[0][0] = 1 ;// 起始点位置:这里以(0,0)为起点
for(int i = 0; i < m; ++i)
{
for(int j = 0; j < n; ++j)
{
if(i == 0 && j == 0) continue;
if(i == 0 || j == 0) dp[i][j] = 1;
else
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];//根据最初定的起点来确定终点
}
};若不想初始化处理首行、首列。此时要避免越界行为,可以开辟(m+1)×(n+1)的矩阵,以(1,1)位置作为起始点。相当于此时i == 0的行和j==0的列是空出来的(引入虚拟节点的写法):
cpp
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m + 1, vector<int>(n + 1));// m+1行,n+1列矩阵
dp[1][1] = 1;// 起始点位置:这里以(1,1)为起点
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++) {
if (i == 1 && j == 1)
continue;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];//实则本质相同,在处理首行、首列时,仍旧只是一条路径
}
return dp[m][n];
}
};4、最长递增子序列(medium)
题源:链接。

4.1、记忆化搜索版
1)、思路分析
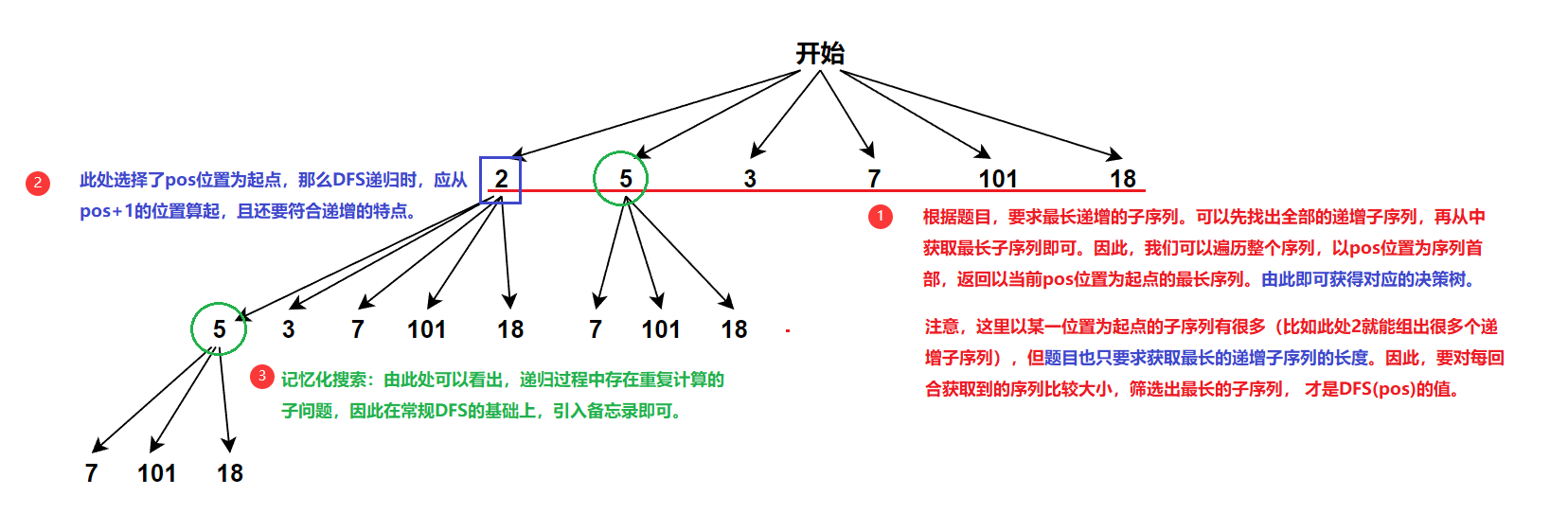
2)、题解
cpp
class Solution {
vector<int> memo;// 备忘录:用于记忆化搜索
public:
int lengthOfLIS(vector<int>& nums) {
memo.resize(nums.size());
int maxsize = 0;
for(int i = 0; i < nums.size(); ++i)
{
maxsize = max(DFS(nums,i),maxsize);
// 不确定以哪一个位置为起点才是最长的递增子序列,因此这里要一一对比一边
}
return maxsize;
}
// pos位置的元素为子序列上一层选定的序列值
int DFS(vector<int>& nums, int pos)
{
// 若当前选择pos的最大子序列曾记录在备忘录内,则直接获取返回
if(memo[pos]) return memo[pos];
// 若备忘录中无记录,则递归查找当前最大子序列
int maxsize = 1;// 选择下一层递归序列值:pos位置处的决策可以有很多分支,我们只要其中长度最大的分支
for(int i = pos + 1; i < nums.size(); ++i)
{
if(nums[i] > nums[pos])// 满足严格递增,可选该值
{
int ret = DFS(nums,i) + 1;// 获取从该值往下递归的结果+将当前pos也算入
maxsize = max(ret,maxsize);// 只记录最大子序列
}
}
memo[pos] = maxsize;// 将当前pos选出的最大子序列记录入备忘录中
return memo[pos];
}
};4.2、动态规划版
1)、思路分析
确定状态表示: dp[pos]表示以pos位置为起点的最长递增子序列长度。
填表顺序: 根据题目,要确定当前pos位置的序列,需要依赖[pos+1, n-1]区间内的元素。因此,这里的填表顺序为从后往前填。
状态转移方程: dp[pos] = max(dp[pos], dp[pos + i] + 1)。由于一个位置处的子序列有多个,而dp[pos]只需要最长递增子序列,因此这里实则是要遍历[pos+1, n-1],比较获取其中最长的递增序列长度,+1即可获得到当前序列的最长长度。
2)、题解
cpp
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
// 动态规划
int n = nums.size();
vector<int> dp(n,1);// 初始化状态表示:自身位置处序列个数为1
int maxsize = 0;// 用于统计最长子序列
// 根据题目,要知道i位置处的最长子序列,则需要知道其后续[i+1,n)位置处的子序列(即,i后应该选谁)
for(int i = n-1; i >= 0; --i)///所以这里的填表顺序是从右到左
{
for(int j = i + 1 ; j < n; ++j)//找[i+1,n)中最长的子序列,+i位置即可获取i处最长子序列
{
if(nums[j] > nums[i])
{
dp[i] = max(dp[i],dp[j] + 1);
}
}
maxsize = max(dp[i],maxsize);//dp[i]统计的是i位置处的最长子序列,maxsize记录的是0~n-1中最长子序列
}
return maxsize;
}
};5、猜数字大小II(medium)
题源:链接。

5.1、题解
1)、思路分析
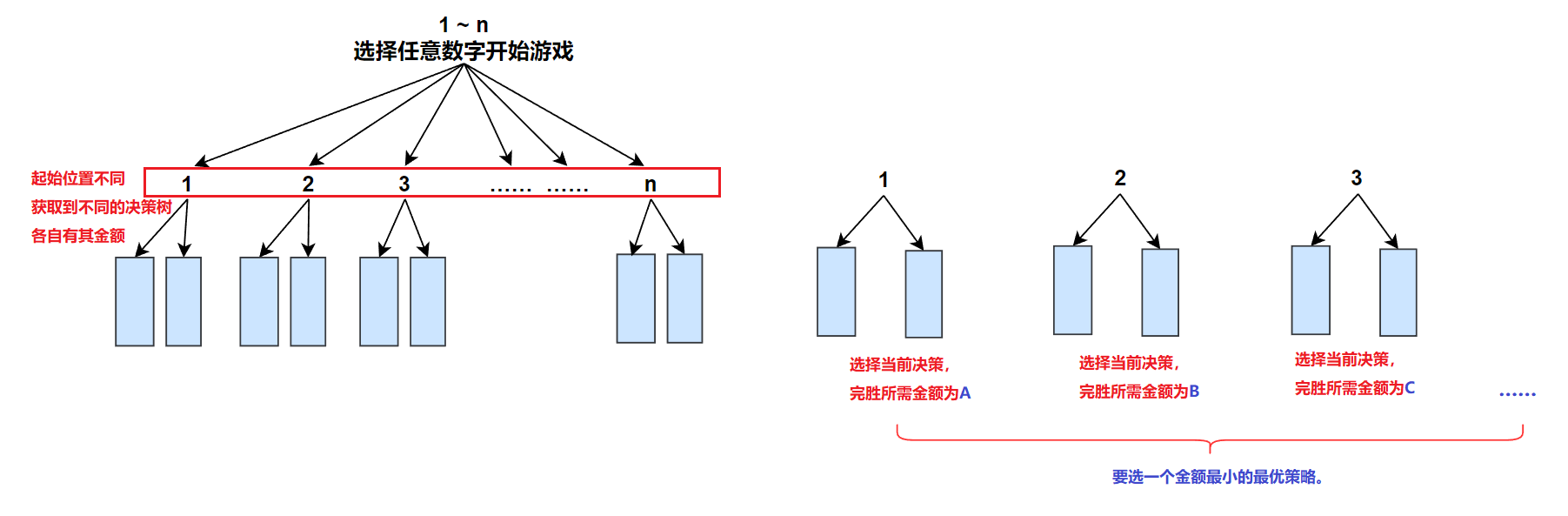
此时实则在模拟猜数字的过程。可将整体分为如下:
1)、对[1,n]个数,在猜数字时可以随机选择其中任意一个数字作为起始决策值 。由此,可获得n棵决策树。当我们选择不同的策略,最终花费的金额各不相同,根据题目要求,要选出能获胜的最小现金数,这就意味着我们要在所有决策树中找最优解(金额最小的决策树) 。
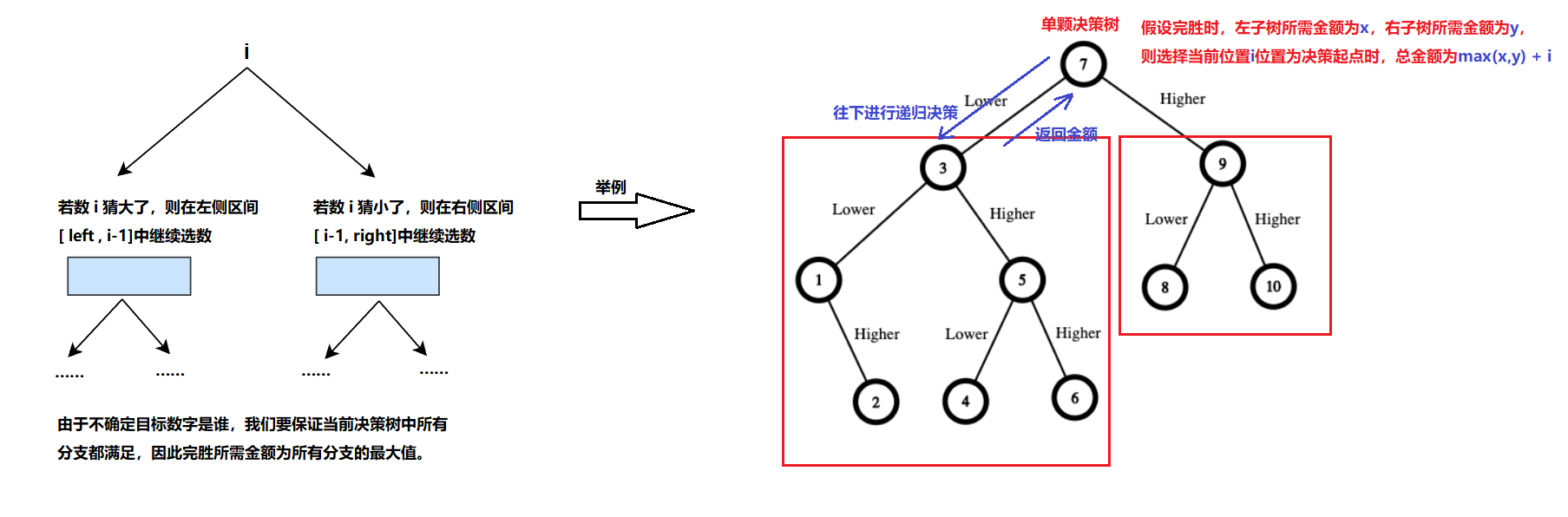
2)、对单棵决策树,由于题目中目标数字是随机的,我们要保证无论给定的是哪一个目标值(即无论哪一条分支),我们的金额都能支付得起,如此才能胜券在握。这就意味着我们要支付的金额为当前单棵决策树的分支最大值。
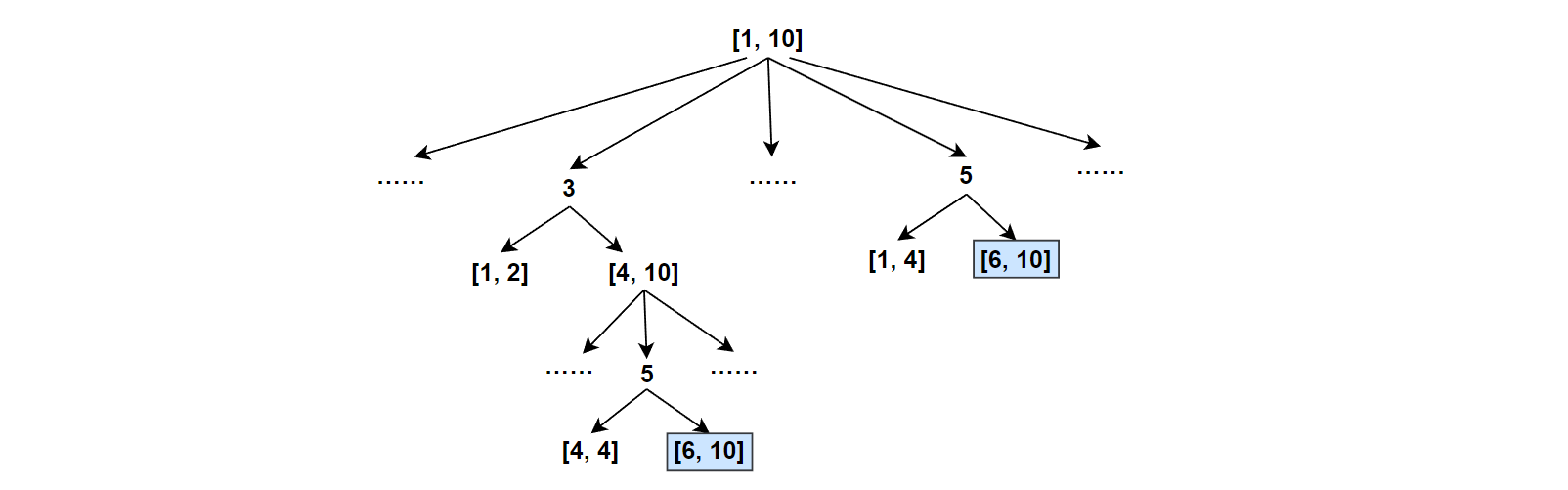
是否可以使用记忆化搜索?
如下图,在递归过程中,每次选出一个数i,若其不满足目标值,则需要在左右区间选数,这里区间[left,right]在选数时会出现重复,故可以使用备忘录。只不过这里备忘录我们记录的是左右两区间,故需要一个二维数组。
2)、题解
cpp
class Solution {
vector<vector<int>> memo;// 备忘录
public:
int getMoneyAmount(int n) {
memo = vector<vector<int>>(n+1,vector<int>(n+1,0));
return DFS(1,n);
}
// 在区间为[left,right]中,选择位置选择一个数,作为决策树的起始位置
int DFS(int left, int right)
{
if(left >= right)
{
return 0;// 选中数字(猜对),无需支付金额;
}
if(memo[left][right]) return memo[left][right];
int minmoney = INT_MAX;// 用于记录所有决策树方案中,所得金额最小的决策方案(因为要是最小值,所以用INT的最大值标记一下)
for(int i = left; i <= right; ++i)// 选择数i作为起始决策位置
{
int x = DFS(left,i-1);// 若数i猜大了:在[left,i-1]继续选数
int y = DFS(i+1,right);// 若数i猜小了:在[i+1,right]继续选数
int ret = max(x,y) + i;// 对单颗决策树,要确保金额能满足即使最糟糕情况也能获胜(故而选择最大分支值+还需要加上当前i位置的金额值)
minmoney = min(minmoney, ret);// 对所有决策树,选择一个使用金额最小的决策方案。
}
memo[left][right] = minmoney;
return minmoney;
}
};6、矩阵中的最长递增路径(hard)
题源:链接。

6.1、题解
1)、思路分析
此题即常规的DFS+一个备忘录。DFS遍历四周的方法我们在先前章节中介绍过,可以使用备忘录是因为对于每个位置(i,j),都有反复经过的可能,因此使用一个二维数组作为备忘录,memo[i][j]表示在[i][j]位置处的最长递增路径长度。
2)、题解
cpp
class Solution {
int memo[201][201];
int m,n;
public:
int longestIncreasingPath(vector<vector<int>>& matrix) {
m = matrix.size(); n = matrix[0].size();
int ret = 0;//用于记录所有起始点中,最长的一条路径。
for(int i = 0; i < m; ++i) // 选择某一点作为路径起始点
{
for(int j = 0; j < n; ++j)
{
ret = max(DFS(matrix,i,j),ret);
}
}
return ret;
}
int dx[4] = {-1, 1, 0, 0};
int dy[4] = {0, 0, -1, 1};
int DFS(vector<vector<int>>& matrix, int i, int j)
{
// 如果备忘录中记录过(i,j)位置的最长递增路径,直接返回
if(memo[i][j] != 0) return memo[i][j];
// 若没记录过,则向四周移动寻找最长递增路径
int maxpath = 1;// 用于统计这四个方向中,路径递增且最长的一次
for(int k = 0; k < 4; ++k)
{
int x = i + dx[k];
int y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[i][j])
{ // 路径合法,且严格递增,则往该方向继续走
maxpath = max(DFS(matrix,x,y)+1, maxpath);
}
}
// 来到此处,说明四周均判断完毕,记录当前(i,j)找出的最长递增路径,返回
memo[i][j] = maxpath;
return maxpath;
}
};Fin、共勉。
