【代码随想录——动态规划——第五周——打家劫舍】

1.打家劫舍

go 复制代码

func rob(nums []int) int {
    n := len(nums)
    dp := make([]int, n+1)
    //初始化
    dp[1] = nums[0]
    for i:=2;i<=n;i++ {
        dp[i] = max(dp[i-1],dp[i-2]+nums[i-1])
    }
    return dp[n]
}

func max(a,b int)int{
    if a>b{
        return a
    }
    return b
}

2.打家劫舍II

区别：区别在于围成了一个圈。可能会出现偷了最后一个，又偷了第一个的情况。

如何避免这种情况：将第一个房子去掉，偷一遍；将最后一个房子去掉，偷一遍

3.打家劫舍III

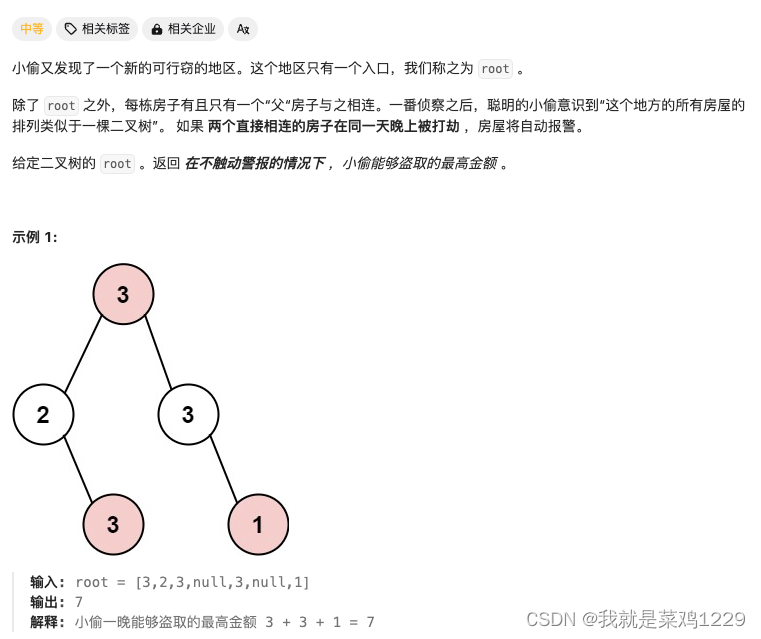
区别：在树结构上进行。被称为树形DP

3.1 暴力递归

使用后续遍历，由于存在大量的重复计算，会导致超时问题。

go 复制代码

func rob(root *TreeNode) int {
    if root==nil{
        return 0
    }
    // 如果当前节点的左右子节点都为空，则返回当前的可偷窃值
    if root.Left==nil && root.Right==nil{
        return root.Val
    }
    // 行窃当前节点
    val1 := root.Val
    if root.Left!=nil {
        val1 += rob(root.Left.Left) + rob(root.Left.Right)
    }
    if root.Right!=nil {
        val1 += rob(root.Right.Left) + rob(root.Right.Right)
    }
    // 不行窃当前节点，代表可以行窃当前节点的儿子节点
    val2 := rob(root.Left) + rob(root.Right)
    return max(val1,val2)
}

3.2 记忆化递推

用map来记住路上的结果，但貌似还是过不了测试用例122。可能是leetcode上的测试用例更新了

go 复制代码

var (
	umap map[*TreeNode]int
)

func rob(root *TreeNode) int {
	umap = make(map[*TreeNode]int)
	
	return robb(root)
}

func robb(root *TreeNode) int {
	if root == nil {
		return 0
	}
	// 如果当前节点的左右子节点都为空，则返回当前的可偷窃值
	if root.Left == nil && root.Right == nil {
		return root.Val
	}
	if val,ok := umap[root];ok{
		return val
	}
	// 行窃当前节点
	val1 := root.Val
	if root.Left != nil {
		val1 += rob(root.Left.Left) + rob(root.Left.Right)
	}
	if root.Right != nil {
		val1 += rob(root.Right.Left) + rob(root.Right.Right)
	}
	// 不行窃当前节点，代表可以行窃当前节点的儿子节点
	val2 := rob(root.Left) + rob(root.Right)
    umap[root] = max(val1, val2);
	return max(val1, val2)
}

3.3 动态规划的解法

融合了递归三部曲和动态规划五部曲

go 复制代码

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func rob(root *TreeNode) int {
    res := robTree(root)
    return max(res[0],res[1])
}


func robTree(cur *TreeNode) []int{
    if cur == nil {
		return []int{0, 0}
	}
    // 后序遍历
    left := robTree(cur.Left)
	right := robTree(cur.Right)
    // 注意顺序：0:不偷，1:去偷
    // 考虑去偷当前的屋子,则该屋子的子节点均不能偷
	robCur := cur.Val + left[0] + right[0]
    // 考虑不去偷当前的屋子，则可以尝试偷子节点
	notRobCur := max(left[0], left[1]) + max(right[0], right[1])
    // 返回当前节点的不偷和偷的情况
    return []int{notRobCur, robCur}
}