目录
一、树的定义
1.1概念
树是n(n>=0)个结点的有限集，
若n=0，称为空树；若n>0，则有且仅有一个特定的称为根的结点，其余结点可分为m(m>=0)个互不相交的有限集T1,T2,....，Tm，其中每一个集合本身又是一棵树，并称为根的子树。
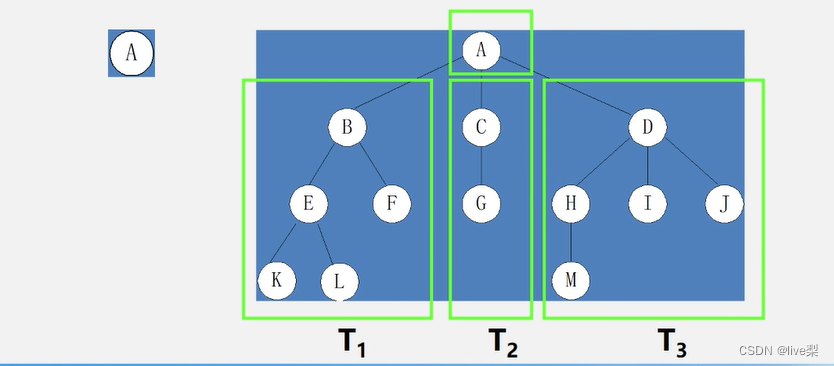
1.2表示方式
树状图、嵌套集合、凹入表示
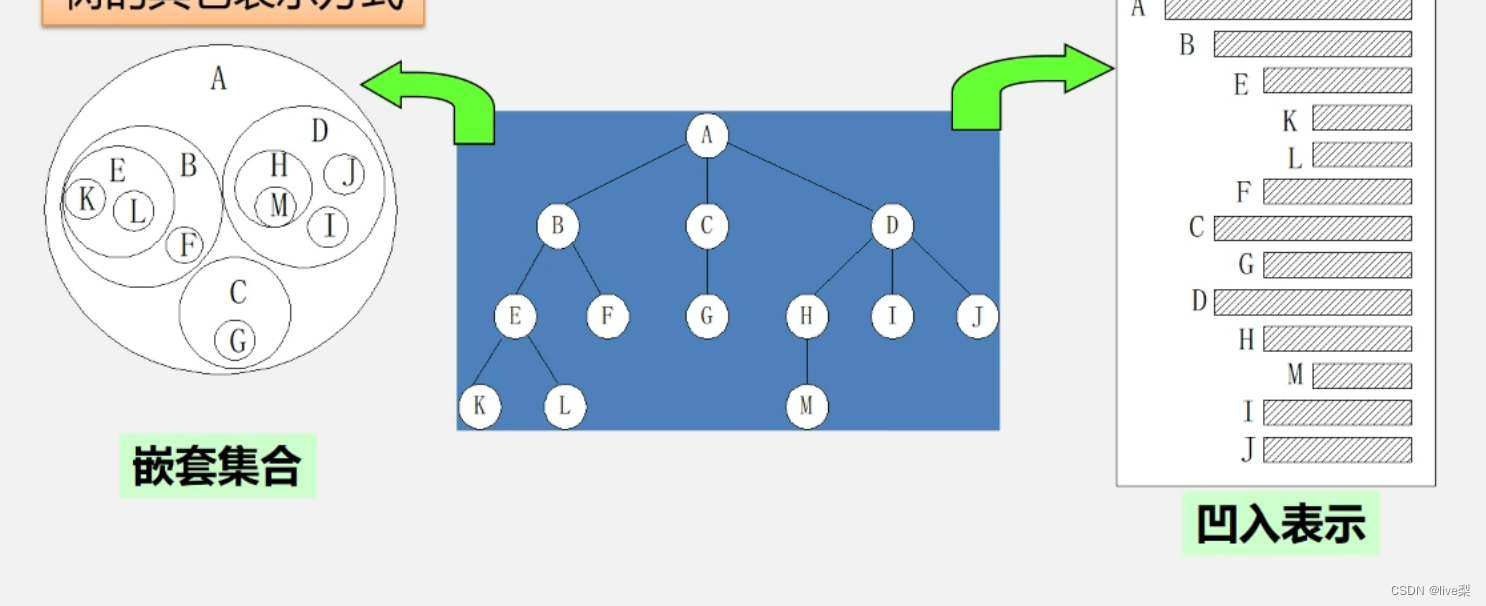
1.3基本术语
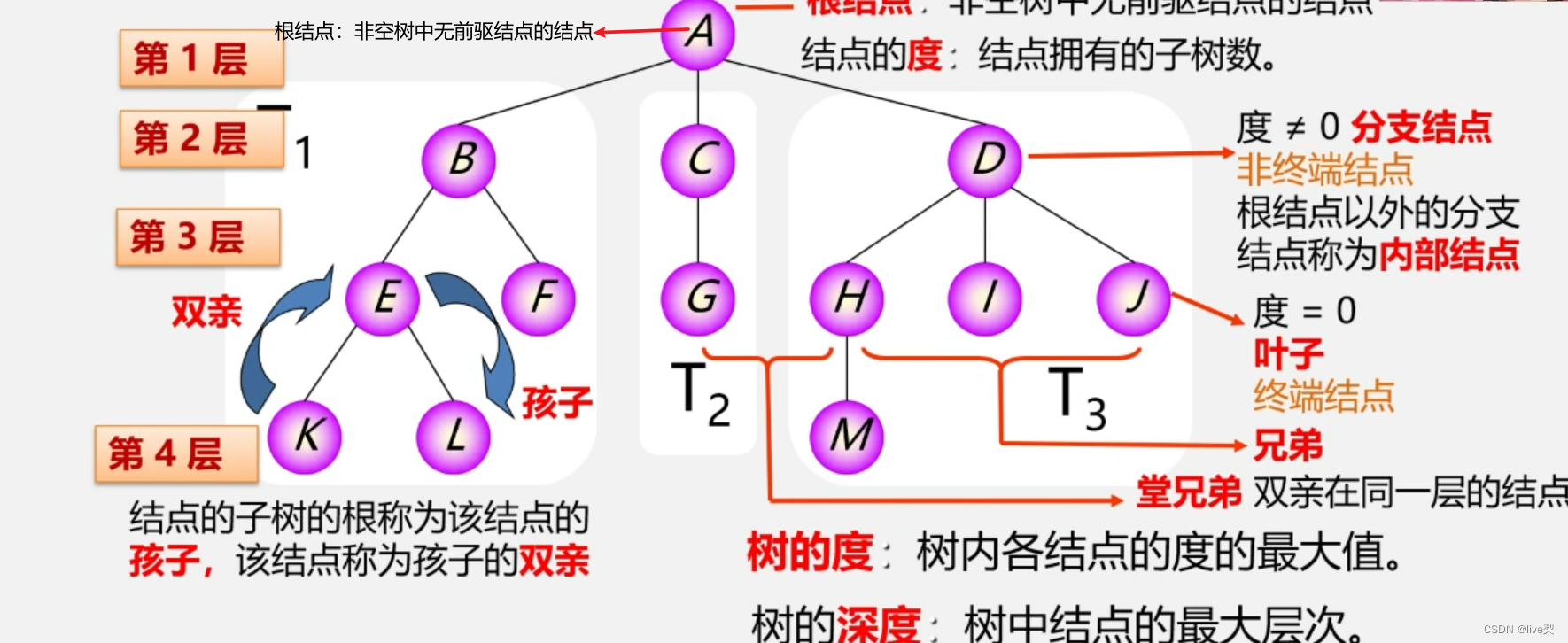
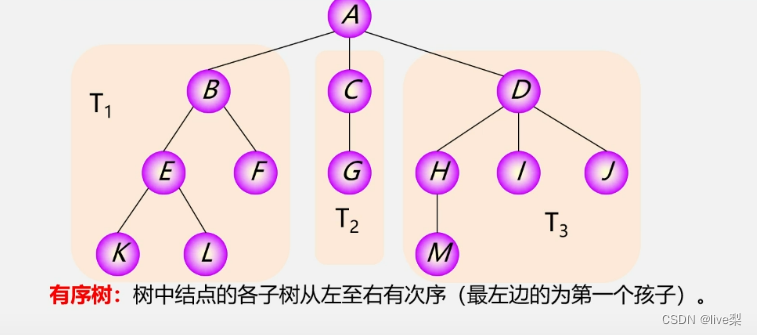无序树：树中结点的各子树无次序。
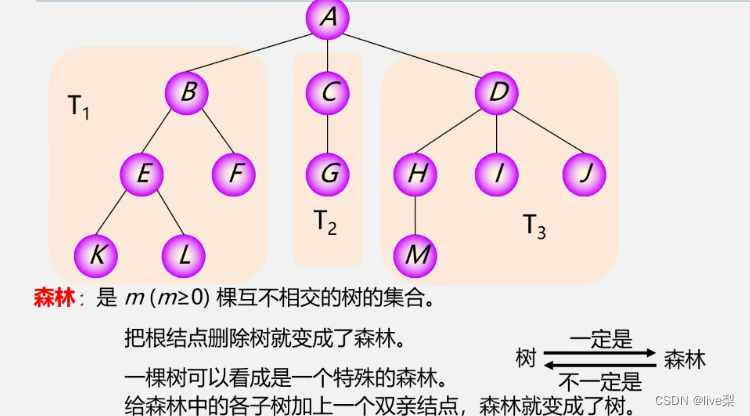
1.4树结构和线性结构的比较
线性结构：一对一；树结构：一对多
二、二叉树的定义
2.1概念
二叉树是n(n>=0)个结点的有限集，它或者是由空集(n=0) 或着由一个根结点及两棵互不相交的左子树和右子树组成。
特点：
①不存在度大于2的结点
②子树有左右之分，次序不能颠倒
③二叉树可以是空集合，根可以有空的左子树或空的右子树
·注：二叉树≠树
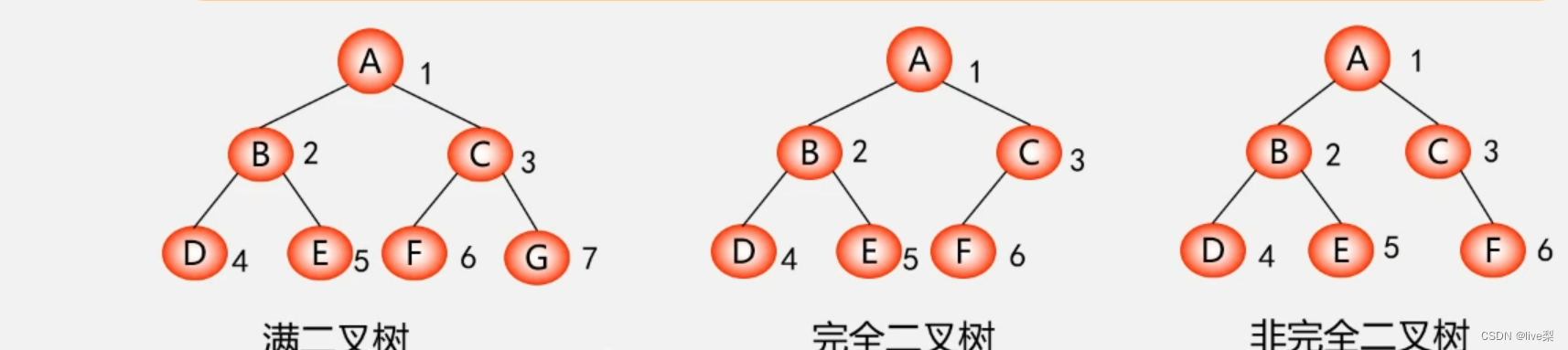
2.2二叉树的5种基本形态
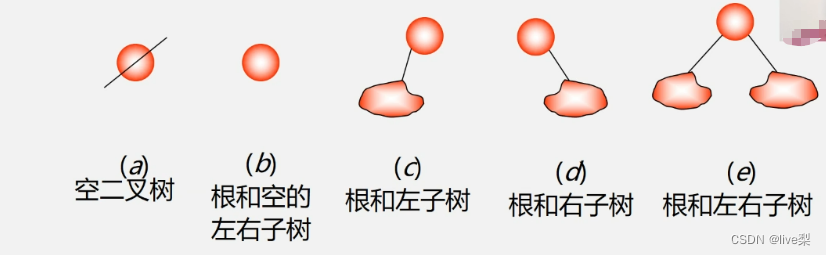
三、二叉树的性质和存储结构
3.1二叉树的性质
性质一： 在二叉树的第i层上**至多有(2^(i-1))**个结点（i>=1)
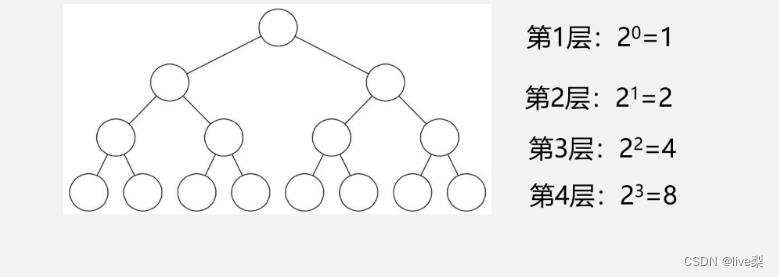
问：第i层上至少有1个结点
性质二： 深度为k的二叉树**至多有（2^k-1）**个结点（k>=1)
问：深度为k时至少有k个结点
性质三： 对任何一棵二叉树T，叶子树为n0，度为2的结点数为n2，则n0=n2+1
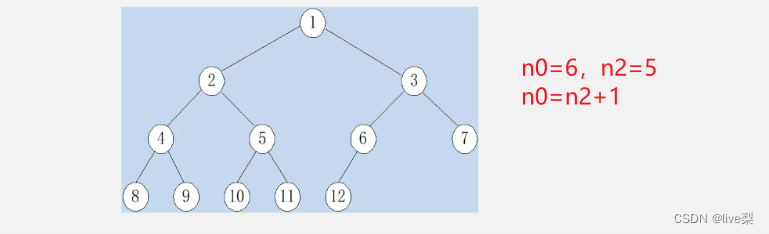
3.1.1满二叉树
一棵深度为k且有(2^k-1)个结点的二叉树称为满二叉树
特点：
①每一层上的结点数都是最大结点数
②叶子结点全部在最底层
（满二叉树在同样深度的二叉树中结点个数和叶子结点个数最多）
编号原则：
从根结点开始，自上而下，自左而右
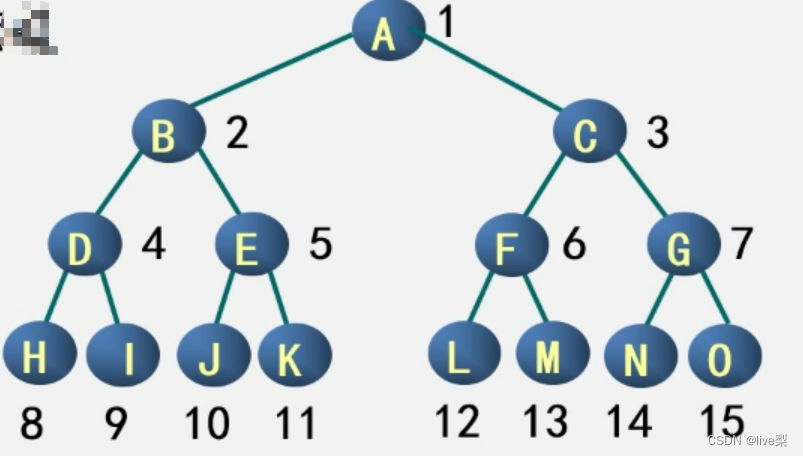
3.1.2完全二叉树
深度为k的具有n个结点的二叉树，当且仅当其每一个结点都与满二叉树中编号为1~n的结点一一对应时，称为完全二叉树
判断下列是否为完全二叉树
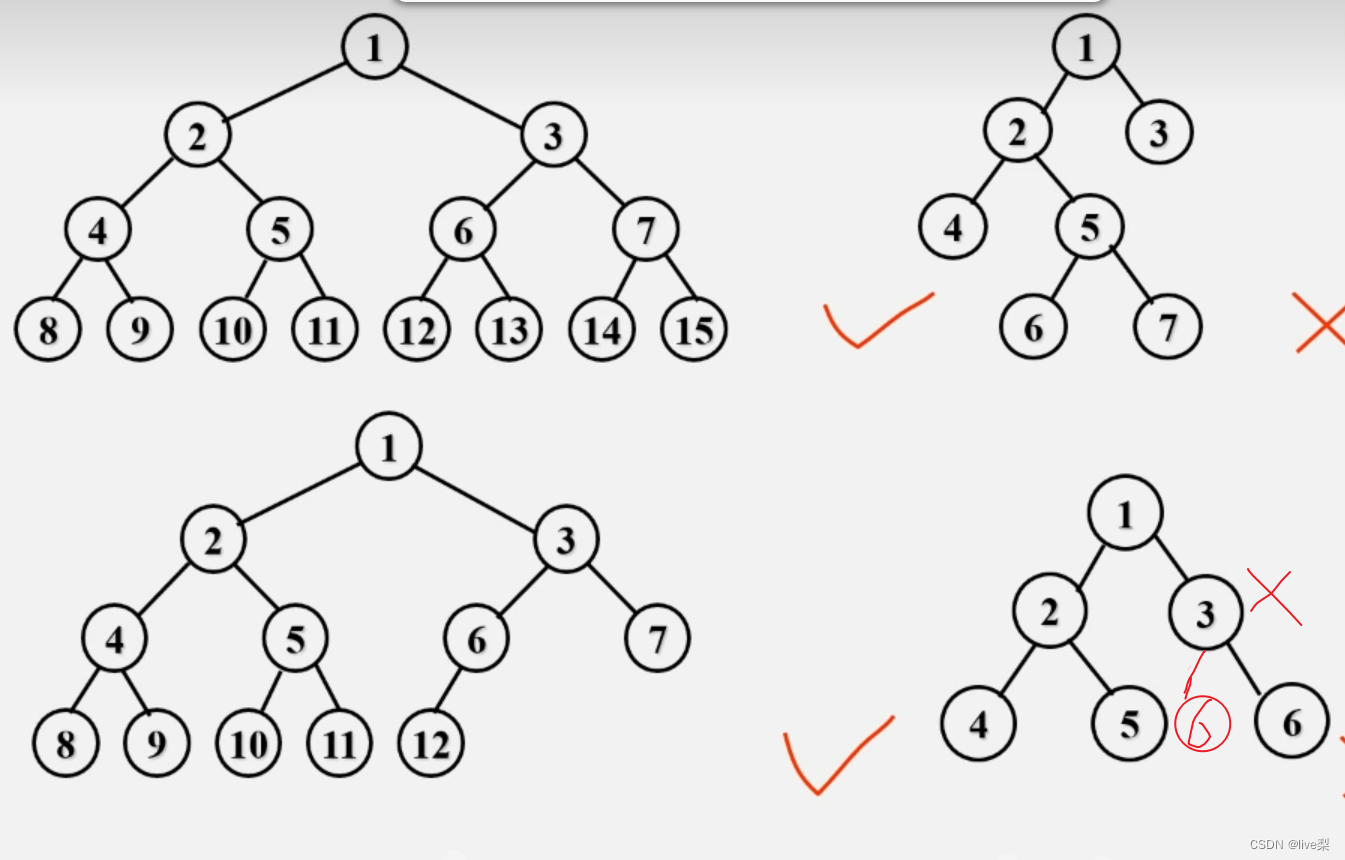
注：在满二叉树中，从最后一个结点开始，连续去掉任意个结点，就是一棵完全二叉树，一定是连续的去掉！
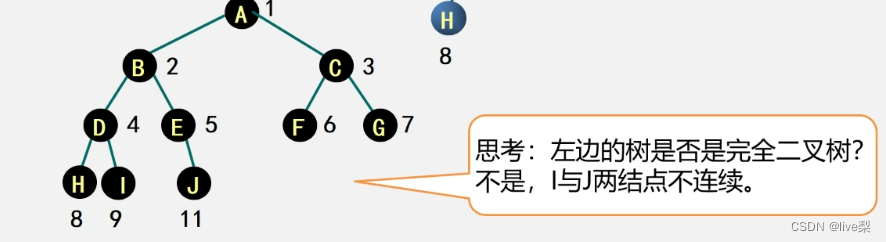
特点：
①叶子只可能分布在层次最大的两层上
②对任一结点，如果其右子树的最大层次为i，那么其左子树的最大层次必为i或i+1
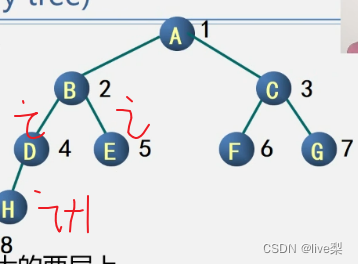
·注：满二叉树一定是完全二叉树，二叉树不一定是满二叉树
**性质四：**具有n个结点的完全二叉树的深度为[log2(n)]+1 ([x]:表示不大于x的最大证书)
**性质五：**如果对一棵有n个结点的完全二叉树（深度为[log2(n)]+1)的结点按层序编号，则对任一结点i(1<=i<=n)，有：
3.2二叉树的存储结构
3.2.1二叉树的顺序存储
实现：按满二叉树的结点层次编号，依次存放二叉树中的数据元素
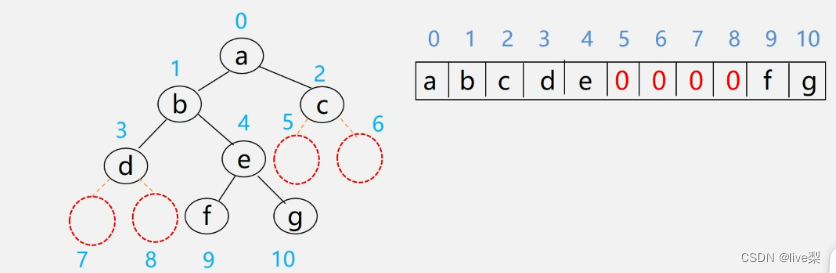
适用情况：满二叉树和完全二叉树
3.2.2二叉树的链式存储
存储结构
①二叉链表：寻找后继
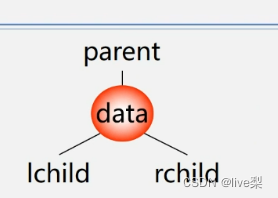
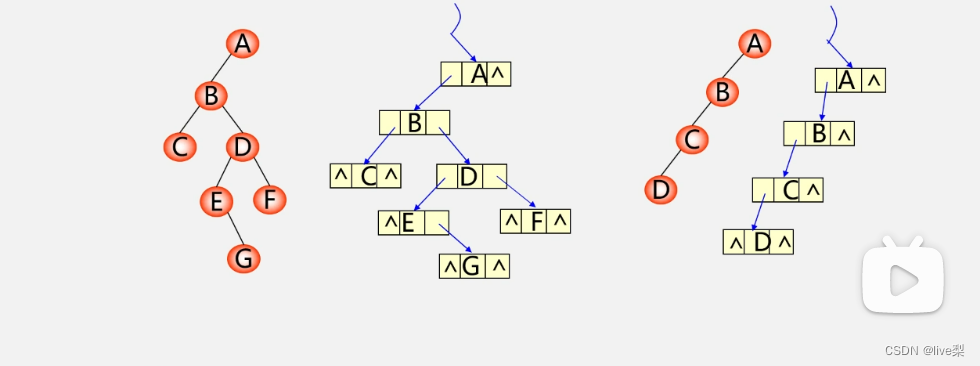
问：在n个结点的二叉链表中，有**(n+1)个空指针域**
n个结点，有2n个链域，除根结点外，每个结点有且仅有一个双亲，所以只会有n-1个结点的链域存放指针，指向非空子女结点，那么空指针域则为(2n-(n-1))=n+1个
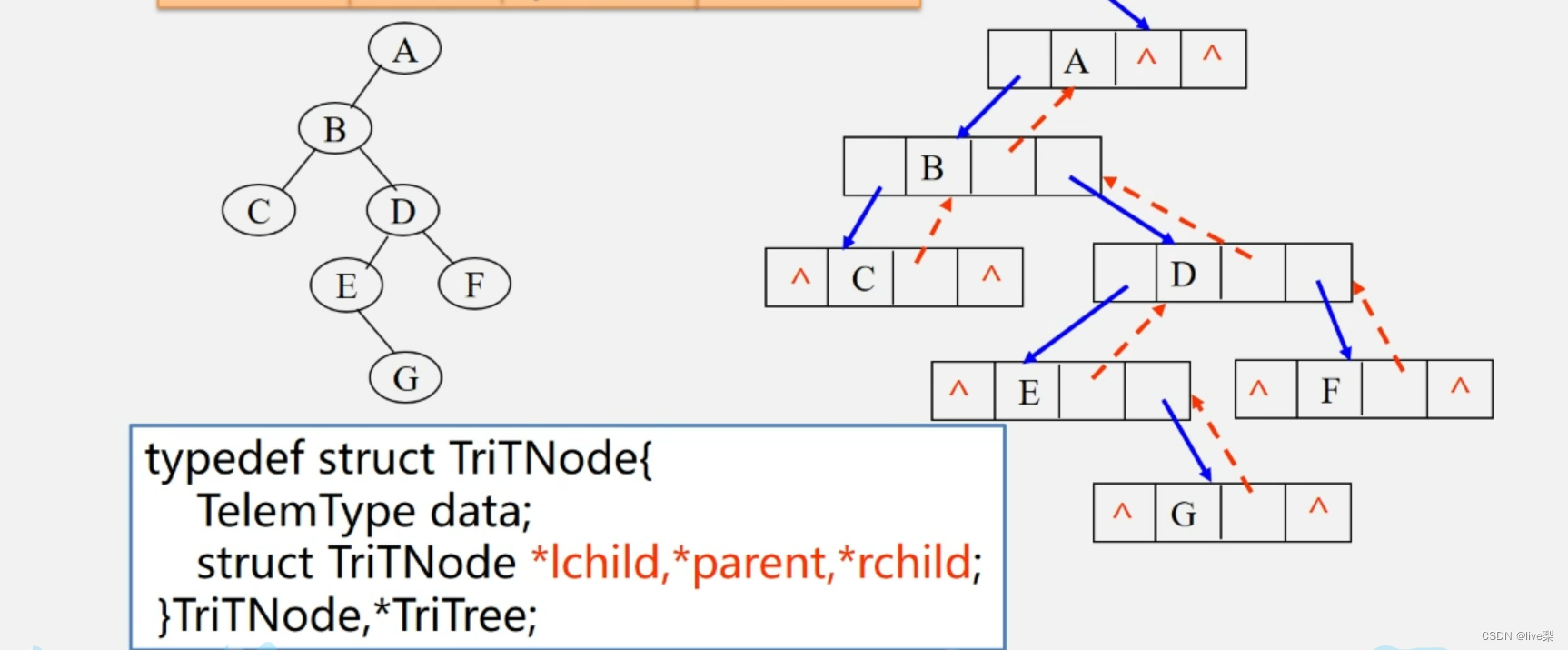
②三叉链表：寻找前驱和后继
