LeetCode-day17-2713. 矩阵中严格递增的单元格数

题目描述
示例
思路
代码

题目描述

给你一个下标从 1 开始、大小为 m x n 的整数矩阵 mat，你可以选择任一单元格作为 起始单元格 。

从起始单元格出发，你可以移动到 同一行或同一列 中的任何其他单元格，但前提是目标单元格的值 严格大于 当前单元格的值。

你可以多次重复这一过程，从一个单元格移动到另一个单元格，直到无法再进行任何移动。

请你找出从某个单元开始访问矩阵所能访问的 单元格的最大数量 。

返回一个表示可访问单元格最大数量的整数。

示例

示例1：

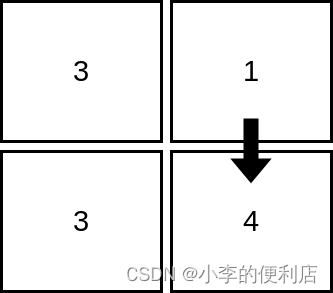
输入：mat = [[3,1],[3,4]]

输出：2

解释：上图展示了从第 1 行、第 2 列的单元格开始，可以访问 2 个单元格。可以证明，无论从哪个单元格开始，最多只能访问 2 个单元格，因此答案是 2 。

示例2：

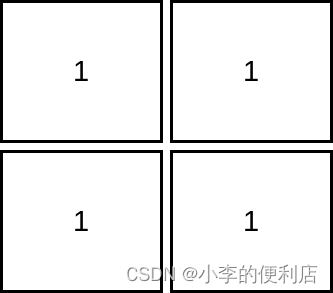
输入：mat = [[1,1],[1,1]]

输出：1

解释：由于目标单元格必须严格大于当前单元格，在本示例中只能访问 1 个单元格。

示例3：

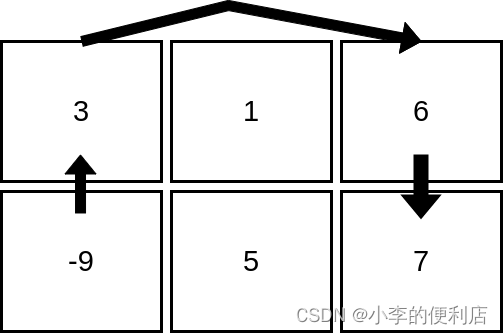
输入：mat = [[3,1,6],[-9,5,7]]

输出：4

解释：上图展示了从第 2 行、第 1 列的单元格开始，可以访问 4 个单元格。可以证明，无论从哪个单元格开始，最多只能访问 4 个单元格，因此答案是 4 。

思路

动态规划。此题为难题~

代码

java 复制代码

public int maxIncreasingCells(int[][] mat) {
        int m = mat.length;
        int n = mat[0].length;
        TreeMap<Integer, List<int[]>> g = new TreeMap<>();
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                g.computeIfAbsent(mat[i][j],k -> new ArrayList<>()).add(new int[]{i,j});
            }
        }

        int ans =0;
        int[] row = new int[m];
        int[] col = new int[n];
        for (List<int[]> pos : g.values()) {
            int[] f = new int[pos.size()];
            for (int k = 0; k < pos.size(); k++) {
                int[] p = pos.get(k);
                int i = p[0];
                int j = p[1];
                f[k] = Math.max(row[i],col[j])+1;
                ans = Math.max(ans,f[k]);
            }
            for (int k = 0; k < pos.size(); k++) {
                int[] p = pos.get(k);
                int i = p[0];
                int j = p[1];
                row[i] = Math.max(row[i],f[k]);
                col[j] = Math.max(col[j],f[k]);
            }
        }
        return ans;
    }