1 高斯滤波原理
1.1 原理
高斯滤波是一种线性平滑滤波技术,主要用于消除图像中的高斯噪声。它的工作原理可以理解为对整幅图像进行加权平均的过程,即每个像素点的值都由其本身和邻域内的其他像素值经过加权平均后得到。
高斯滤波实质上是一种信号的滤波器,其用途是信号的平滑处理。在数字图像处理中,噪声是最大的问题之一,由于误差会累计传递,因此高斯滤波器被广泛应用于图像去噪过程,以获取信噪比SNR较高的图像,从而更真实地反映原始信号。
1.2 公式
高斯滤波的核心是高斯函数,其公式在一维情况下表示为:
其中,(G(x)) 表示高斯函数在 (x) 处的值,(\sigma) 是标准差,它决定了高斯函数的宽度,从而影响了滤波的强弱程度。标准差越大,滤波程度越强,滤波效果越明显。
在二维图像处理中,高斯滤波使用的高斯核是两个一维高斯函数的乘积,形式如下:
其中,((x, y)) 是图像中的像素坐标,(\sigma) 是标准差。高斯核是对连续高斯函数的离散近似,通常通过对高斯曲面进行离散采样和归一化得出。这里,归一化指的是卷积核所有元素之和为1。
1.3 实现方法
高斯滤波的实现通常使用卷积操作,即将高斯函数(或高斯核)应用到图像上,通过计算每个像素点与其邻域内像素点的加权平均灰度值来替代该像素点的原始值。具体操作为:用一个模板(或称卷积核、掩模)扫描图像中的每一个像素,用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。
高斯滤波在计算机视觉和图像处理中是最常见的操作之一,它有两种主要的实现方式:一是使用离散化窗口滑窗卷积;另一种则是通过傅里叶变换来实现。
2 中值滤波去噪原理
2.1 原理
中值滤波是一种非线性平滑技术,主要用于消除图像或信号中的噪声,特别是椒盐噪声。其基本原理是:将数字图像或数字序列中一点的值用该点的一个邻域中各点值的中值代替,让周围的像素值接近真实值,从而消除孤立的噪声点。
中值滤波的核心思想是认为噪声像素的值与周围像素值存在显著差异,因此通过取周围像素值的中值可以有效减少噪声的影响。同时,中值滤波在滤除噪声的同时,能够保护信号的边缘,使之不被模糊,这是线性滤波方法所不具备的。
2.2 步骤
- 遍历图像的每个像素点,选择一个特定的邻域大小(如3x3、5x5等),该邻域大小可以根据实际需要进行调整。
- 将邻域内的像素值按照大小进行排序,生成单调上升(或下降)的二维数据序列。
- 将排序后的中值作为当前像素的新值,用于替代原始的像素值或噪声像素值。
2.3 公式
公式一般用来表示二维图像中的中值滤波操作。假设我们有一个滑动窗口,其尺寸为m×m(m为奇数),窗口覆盖下的像素邻域像素值序列长度为m²。序列中的每个元素对应于窗口内的一个像素值。将这些像素值进行排序后,取中间值作为窗口中心像素的新值。
用数学公式表示如下:
其中,g(x, y)表示中值滤波后图像在(x, y)处的像素值,f(x, y)表示原始图像在(x, y)处的像素值,v = (m-1)/2,med表示取中值操作。
这个公式描述了中值滤波的基本操作过程,即通过在图像上滑动一个固定大小的窗口,并将窗口内像素值的中值作为窗口中心像素的新值,来实现对图像的平滑去噪处理。
3.代码
Matlab
%% 图像预处理-高斯滤波与图像去噪
I = imread('test.jpeg');
if size(I, 3) == 3
% 如果是彩色图像,转换为灰度图像
I = rgb2gray(I);
end
I = im2double(I); % 将图像转换为双精度,范围在[0, 1]
% 对图像进行高斯滤波
h = fspecial('gaussian', [5 5], 1); % 创建一个5x5的高斯滤波器,标准差为1
I_gaussian = imfilter(I, h);
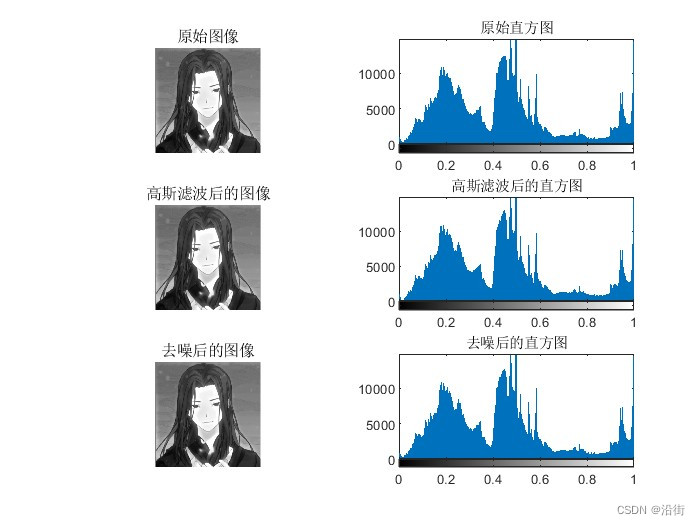
% 绘制原始图像和原始直方图
figure;
subplot(3, 2, 1),imshow(I);
title('原始图像');
subplot(3, 2, 2),imhist(I);
title('原始直方图');
% 绘制高斯滤波后的图像和对应的直方图
subplot(3, 2, 3),imshow(I_gaussian);
title('高斯滤波后的图像');
subplot(3, 2, 4),imhist(I_gaussian);
title('高斯滤波后的直方图');
% 去噪使用中值滤波
I_denoised = medfilt2(I); % 使用中值滤波进行去噪
% 绘制去噪后的图像和对应的直方图
subplot(3, 2, 5),imshow(I_denoised);
title('去噪后的图像');
subplot(3, 2, 6),imhist(I_denoised);
title('去噪后的直方图'); 4 运行结果