LeetCode 1164, 125, 94

A22742024-06-23 23:51

目录

1164. 指定日期的产品价格

题目链接

1164. 指定日期的产品价格

表

  • 表Products的字段为product_id、new_price和change_date。

要求

  • 编写一个解决方案，找出在 2019-08-16 时全部产品的价格，假设所有产品在修改前的价格都是 10 。
  • 以 任意顺序 返回结果表。

知识点

  1. in：有一次限制多个字段的功能。例如：
sql 复制代码 
where
	(id, num)
in (
	select
		id,
		num
	from
		tb_stock
)

此语句将id和num限制到从tb_stock表中查询到的结果，注意 ()中的字段数 与 子表查询到的字段数 必须是相同的。

  1. max()：求最大值的函数。
  2. ifnull()：共传入两个参数，如果第一个参数是null，则返回第二个参数。例如ifnull(null, 'no')将会返回no。
  3. left join：左连接，将 左表的所有数据 和 右表与左表的交集数据 查询出来。
  4. distinct：对字段的相同值进行去重。

思路+代码

找出在 2019-08-16 时全部产品的价格，

所以需要先查出更新的产品的在 2019-08-16 之前的最迟更新日期max_change_date，

sql 复制代码 
select
	product_id,
	max(change_date) max_change_date
from
	Products
where
	change_date <= '2019-08-16'
group by
	product_id

然后再求出这些产品在最迟更新日期max_change_date更新的价格new_price，

sql 复制代码 
select
	product_id,
	new_price
from
	Products
where (
	product_id,
	change_date
) in (
	select
		product_id,
		max(change_date) max_change_date
	from
		Products
	where
		change_date <= '2019-08-16'
	group by
		product_id
)

最后查出所有的产品id，然后将查到new_price的产品的价格返回，将没有查到new_price的产品按价格为10返回。注意，由于要查出所有的产品id，然后再与 查到new_price的部分 产品id 进行多表查询，所以得使用 外连接 ，本题使用了 左外连接 left join。

sql 复制代码 
select
    id_cnt.product_id,
    ifnull(new_price, 10) price
from (
        select
            distinct product_id
        from
            Products
    ) id_cnt
left join (
        select
            product_id,
            new_price
        from
            Products
        where (
        	product_id,
            change_date
        ) in (
            select
                product_id,
                max(change_date) max_change_date
            from
                Products
            where
                change_date <= '2019-08-16'
            group by
                product_id
        )
    ) price_cnt
on
    id_cnt.product_id = price_cnt.product_id

125. 验证回文串

题目链接

125. 验证回文串

标签

双指针 字符串

简单版

思路

本题的思路很明确，先将所有大写字符转换为小写字符，并移除所有非字母数字字符，然后再对剩下的字符串进行是否是回文串的判断。

是否是回文串可以使用双指针的做法，左指针left从字符串头部向尾部遍历，右指针right从字符串尾部向头部遍历，直到 两个指针相遇 或 左指针的值 比 右指针的值 大，如果发现左指针和右指针指向的字符不相同，则返回false；若能退出遍历，则说明这个字符串是一个回文串，返回true。

代码

java 复制代码 
class Solution {
    public boolean isPalindrome(String s) {
        s = s.toLowerCase(); // 将所有大写字符转换为小写字符
        s = removeNonAlphaOrDight(s); // 移除所有非字母数字字符
        char[] chars = s.toCharArray();
        int left = 0, right = chars.length - 1;
        while (left < right) {
            if (chars[left] != chars[right]) {
                return false;
            }
            left++;
            right--;
        }
        return true;
    }
    // 移除字符串s中的所有非字母数字字符
    private String removeNonAlphaOrDight(String s) {
        char[] chars = s.toCharArray();
        StringBuilder builder = new StringBuilder();
        for (char ch : chars) {
            if (Character.isLetterOrDigit(ch)) {
                builder.append(ch);
            }
        }
        return builder.toString();
    }
}

复杂版

思路

简单版的执行用时比较长，因为对源字符串进行了 转换 和 移除 的操作。如果不想浪费这些时间，就得在 指针 和 判断 这两个点下功夫：当指针指向 非字符数字字符(空格也是非字符数字字符) 时跳过这个字符，并且需要 在判断左右指针指向的字符是否相等前 将字符转化为小写。

代码

java 复制代码 
class Solution {
    public boolean isPalindrome(String s) {
        char[] chars = s.toCharArray();
        int left = 0, right = chars.length - 1;
        while (left < right) {
            if (!Character.isLetterOrDigit(chars[left])) {
                left++;
                continue;
            }
            if (!Character.isLetterOrDigit(chars[right])) {
                right--;
                continue;
            }
            
            char leftChar = Character.toLowerCase(chars[left]);
            char rightChar = Character.toLowerCase(chars[right]);
            if (leftChar != rightChar) {
                return false;
            }
            left++;
            right--;
        }
        return true;
    }
}

94. 二叉树的中序遍历

题目链接

94. 二叉树的中序遍历

标签

栈 树 深度优先搜索 二叉树

递归

思路

中序遍历就是先遍历本节点的左子节点，然后处理本节点的值，最后遍历本节点的右子节点。

例如对于下面这个二叉树：

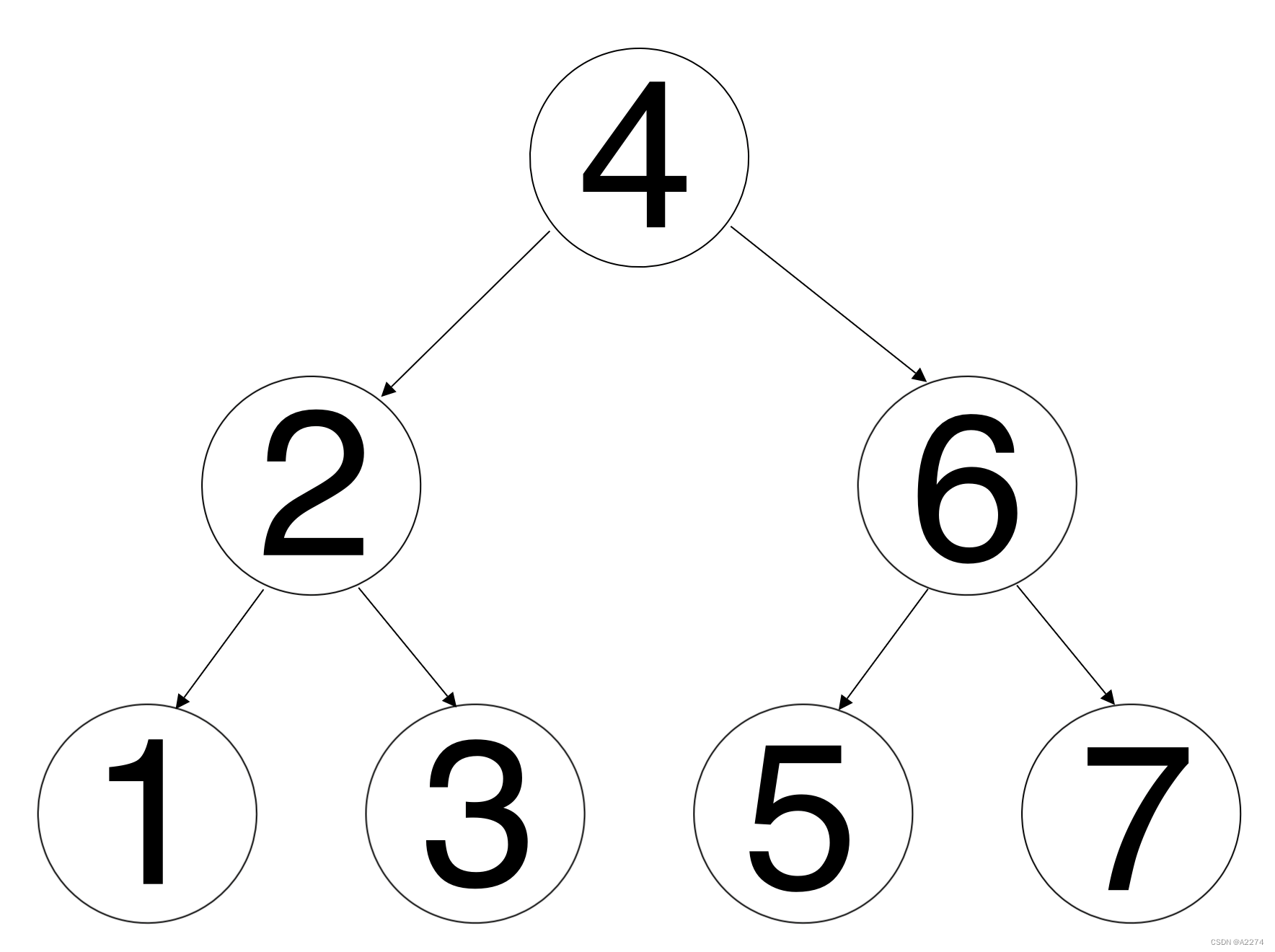
中序遍历这个二叉树的结果是[1, 2, 3, 4, 5, 6, 7]，过程为：

从节点4开始

往节点2走

往节点1走

往节点1的左子节点走，发现是null

返回到节点1，输出节点1的值

往节点1的右子节点走，发现是null

返回到节点1，返回到节点2，输出节点2的值

往节点3走

往节点3的左子节点走，发现是null

返回到节点3，输出节点3的值

往节点3的右子节点走，发现是null

返回到节点2，返回到节点4，输出节点4的值

往节点6走

往节点5走

往节点5的左子节点走，发现是null

返回到节点5，输出节点5的值

往节点5的右子节点走，发现是null

返回到节点6，输出节点6的值

往节点7走

往节点7的左子节点走，发现是null

返回到节点7，输出节点7的值

往节点7的右子节点走，发现是null

返回节点6，返回节点4，完毕

理解如上的过程后就清晰了，使用递归将此过程模拟一遍就是如下代码：

代码

java 复制代码 
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        inorder(root, res);
        return res;
    }
    private void inorder(TreeNode curr, List<Integer> res) {
        if (curr == null) { // 如果遇到空节点
            return; // 直接返回
        }
        inorder(curr.left, res); // 先遍历左子节点
        res.add(curr.val); // 再处理本节点的值
        inorder(curr.right, res); // 最后遍历右子节点
    }
}

迭代

思路

使用递归能做出来的题，使用迭代也可以，只不过迭代比较难罢了。

对二叉树的前序遍历、中序遍历和后序遍历本质上都是深度优先搜索 ，即遍历时不是一层一层遍历，而是顺着一个方向走到头，然后再回过头来处理这些值 。对于这样的遍历，可以使用 栈 将递归转化为迭代：顺着一个方向走时先将这些节点存起来，然后再弹出最近保存的节点进行处理。

递归的思想和迭代的思想是一样的，只不过实现方式不同，迭代时得分类讨论：

当遍历的节点curr不为null时，就先将本节点curr加入栈stack中，然后往左子节点curr.left遍历；

否则遍历的节点curr为null，此时还得根据 最近一次加入栈的节点peek = stack.peek() 的右子节点的不同进行分类讨论。

只有在没遍历右子节点时才需要对本节点进行操作(这是中序遍历的思想) ，当它的右子节点peek.right不是最近一次弹出栈的节点pop时，说明此时还没有遍历右子节点，应该操作本节点，然后弹出并记录本节点pop = stack.pop()；当它的右子节点peek.right为null时，也可以将其看作没有遍历右子节点的情况，操作本节点，然后弹出并记录本节点pop = stack.pop()；如果不是以上两种情况，则是peek.right是最近一次弹出栈的节点pop的情况，这意味着已经遍历过右子节点了，只需要弹出并记录本节点pop = stack.pop()即可。

分类讨论到处结束，如果还不是很懂，就看看代码吧。

代码

java 复制代码 
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        LinkedList<TreeNode> stack = new LinkedList<>();
        List<Integer> res = new ArrayList<>();
        TreeNode curr = root; // 当前节点
        TreeNode pop = null; // 最近一次弹出栈的节点
        while (!stack.isEmpty() || curr != null) {
            if (curr != null) { // 如果这个节点不为null
                stack.push(curr); // 将这个节点保存到栈中
                curr = curr.left; // 让节点往左子节点走
            } else { // 此时对应某节点的左子节点为null的情况
                TreeNode peek = stack.peek(); // 查看最近一次加入栈中的节点
                if (peek.right == null) { // 没有右子节点 也算 右子节点没有遍历
                    res.add(peek.val); // 处理本节点的值
                    pop = stack.pop(); // 将本节点从栈中弹出，并保存它
                } else if (peek.right != pop) { // 此时还没有遍历右子节点
                    res.add(peek.val); // 处理本节点的值
                    curr = peek.right; // 将本节点从栈中弹出，并保存它
                } else { // 此时 最近一次弹出栈的节点 是 最近一次加入栈的节点的右子节点，表示已经处理完了右子节点
                    pop = stack.pop(); // 将本节点弹出，并保存它
                }
            }
        }
        return res;
    }
}
相关推荐
远歌已逝8 分钟前
维护在线重做日志(二)
数据库·oracle
qq_433099401 小时前
Ubuntu20.04从零安装IsaacSim/IsaacLab
数据库
Dlwyz1 小时前
redis-击穿、穿透、雪崩
数据库·redis·缓存
Theodore_10222 小时前
4 设计模式原则之接口隔离原则
java·开发语言·设计模式·java-ee·接口隔离原则·javaee
网易独家音乐人Mike Zhou3 小时前
【卡尔曼滤波】数据预测Prediction观测器的理论推导及应用 C语言、Python实现（Kalman Filter）
c语言·python·单片机·物联网·算法·嵌入式·iot
工业甲酰苯胺3 小时前
Redis性能优化的18招
数据库·redis·性能优化
冰帝海岸3 小时前
01-spring security认证笔记
java·笔记·spring
世间万物皆对象4 小时前
Spring Boot核心概念：日志管理
java·spring boot·单元测试
没书读了4 小时前
ssm框架-spring-spring声明式事务
java·数据库·spring
小二·4 小时前
java基础面试题笔记（基础篇）
java·笔记·python
热门推荐
01(欧拉)openEuler系统添加网卡文件配置流程、(欧拉)openEuler系统手动配置ipv6地址流程、(欧拉)openEuler系统网络管理说明02PyTorch机器学习实现液态神经网络03【HarmonyOS】HUAWEI DevEco Studio 下载地址汇总04玄机平台应急响应—webshell查杀05Coze扣子平台完整体验和实践（附国内和国际版对比）06Ubuntu 20.04使用Livox mid 360 测试 FAST_LIO07【目标跟踪】相机运动补偿08Unity中PICO实现 隔空取物 和 接触抓取物体09RAG 实践- Ollama+RagFlow 部署本地知识库10怎样让音频速度变慢？请跟随以下方法进行操作