基于matlab的图像多层小波变换

1 代码

Matlab 复制代码
%% %%  清空环境变量
warning off             % 关闭报警信息
close all               % 关闭开启的图窗
clear                   % 清空变量
clc                     % 清空命令行

%% 读取图像  
originalImage = imread('test.jpg'); % 替换为您的图像文件名  
originalImage = rgb2gray(originalImage); % 转换为灰度图像  
originalImage = im2double(originalImage); % 转换为双精度  
  
% 初始化变量以存储每一层的近似和细节系数  
LL = originalImage;  
coeffs = {}; % 存储每一层的系数  
%% 对图像进行多层二维小波分解  
numLevels = 3; % 假设进行3层分解  
for level = 1:numLevels  
    [LL, LH, HL, HH] = dwt2(LL, 'haar'); % 使用'haar'小波进行分解  
    coeffs{level} = {LL, LH, HL, HH}; % 存储当前层的系数  
end  
  
%% 绘制每层小波分解的结果  
% figure;  
figure('Position', [100 100 800 600]);
for level = 1:numLevels  
    subplot(numLevels, 4, (level-1)*4+1); imshow(coeffs{level}{1}, []); title(['Approximation after level ', num2str(level)]);  
    subplot(numLevels, 4, (level-1)*4+2); imshow(coeffs{level}{2}, []); title(['Horizontal Detail after level ', num2str(level)]);  
    subplot(numLevels, 4, (level-1)*4+3); imshow(coeffs{level}{3}, []); title(['Vertical Detail after level ', num2str(level)]);  
    subplot(numLevels, 4, (level-1)*4+4); imshow(coeffs{level}{4}, []); title(['Diagonal Detail after level ', num2str(level)]);  
end  
%% 对每层进行重构并绘制  
figure;  
for level = numLevels:-1:1  
    if level == numLevels  
        % 最顶层只有近似系数，直接显示  
        reconstructedImage = coeffs{level}{1};  
    else  
        % 使用当前层的四个系数进行重构  
        reconstructedImage = idwt2(coeffs{level}{1}, coeffs{level}{2}, coeffs{level}{3}, coeffs{level}{4}, 'haar');  
    end  
    subplot(numLevels, 1, numLevels-level+1);  
    imshow(reconstructedImage, []);  
    title(['Reconstructed Image after level ', num2str(level)]);  
end
  
%% 使用每一层的近似系数进行逆变换并绘制结果
figure;  
for level = numLevels:-1:1  
    % 仅使用当前层的近似系数进行逆变换  
    if level == 1  
        invTransformedImage = coeffs{level}{1}; % 第一层直接就是原图或近似  
    else  
        % 使用当前层的近似系数和前几层的空细节系数进行逆变换（模拟仅使用近似系数）  
        invTransformedImage = idwt2(coeffs{level}{1}, [], [], [], 'haar');  
        for i = level-1:-1:1  
            invTransformedImage = idwt2(invTransformedImage, [], [], [], 'haar'); % 继续添加空细节系数进行逆变换  
        end  
    end  
    subplot(numLevels, 1, numLevels-level+1);  
    imshow(invTransformedImage, []);  
    title(['Inverse Transformed Image using Approx. after level ', num2str(level)]);  
end    
%% 绘制各个小波系数直方图  
figure;  
for level = 1:numLevels  
    subplot(numLevels, 1, level);  
    imhist(coeffs{level}{1}); % 绘制每一层近似系数的直方图  
    title(['Histogram of Approximation Coefficients after level ', num2str(level)]);  
end
2 运行结果

图1 各层小波分解的近似与分量
图2 各层重构结果
图3 各层逆变换结果
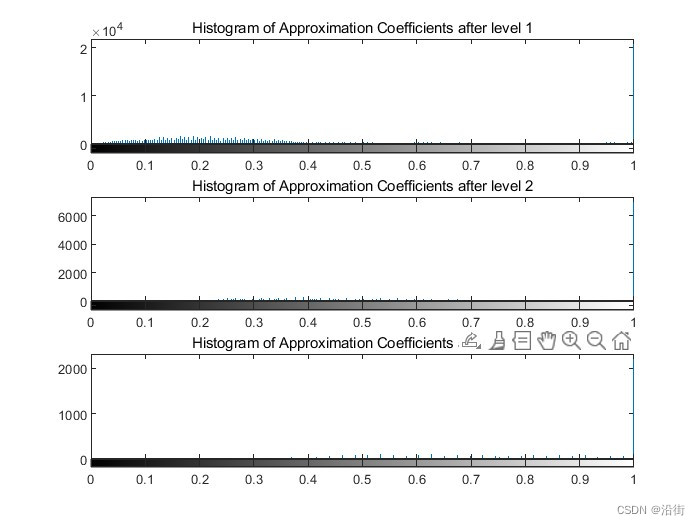
图4 各个小波系数直方图