Java模拟马尔可夫链类问题的验证

马尔可夫链（Markov Chain, MC）是概率论和数理统计中具有马尔可夫性质（Markov property）且存在于离散的指数集（index set）和状态空间（state space）内的随机过程（stochastic process） $1-2$ 。适用于连续指数集的马尔可夫链被称为马尔可夫过程（Markov process），但有时也被视为马尔可夫链的子集，即连续时间马尔可夫链（Continuous-Time MC, CTMC），与离散时间马尔可夫链（Discrete-Time MC, DTMC）相对应，因此马尔可夫链是一个较为宽泛的概念 $2$ 。

马尔可夫链可通过转移矩阵和转移图定义，除马尔可夫性外，马尔可夫链可能具有不可约性、常返性、周期性和遍历性。一个不可约和正常返的马尔可夫链是严格平稳的马尔可夫链，拥有唯一的平稳分布。遍历马尔可夫链（ergodic MC）的极限分布收敛于其平稳分布 $1$ 。

马尔可夫链可被应用于蒙特卡罗方法中，形成马尔可夫链蒙特卡罗（Markov Chain Monte Carlo, MCMC） $2-3$ ，也被用于动力系统、化学反应、排队论、市场行为和信息检索的数学建模。此外作为结构最简单的马尔可夫模型（Markov model），一些机器学习算法，例如隐马尔可夫模型（Hidden Markov Model, HMM）、马尔可夫随机场（Markov Random Field, MRF）和马尔可夫决策过程（Markov decision process, MDP）以马尔可夫链为理论基础 $4$ 。

马尔可夫链的命名来自俄国数学家安德雷·马尔可夫（Андрей Андреевич Марков）以纪念其首次提出马尔可夫链和对其收敛性质所做的研究 $5$ 。

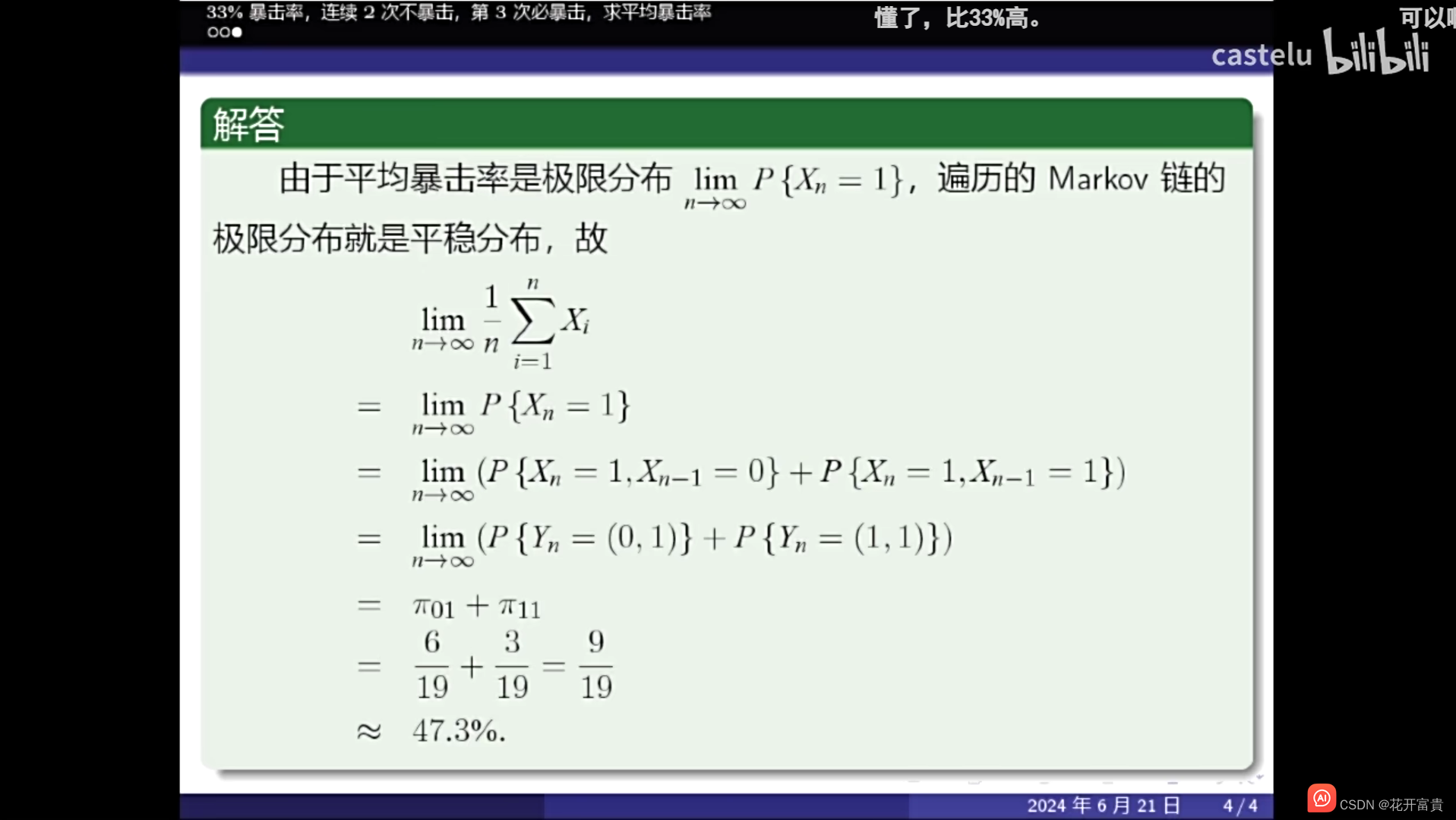
问题概述

注意：此图片引用了b站up主的视频视频源地址视频源地址https://www.bilibili.com/video/BV1ir421F7nq?vd_source=0517d752c26aa2e7b4afc5fdf2257813

主要思路：随机生成大量数据然后进行分析

Java代码部分

java 复制代码

import java.util.ArrayList;
import java.util.List;
import java.util.Random;
public class 暴击 {
    public static void main(String[] args) {
        Random random = new Random();
        List<Integer> integers = new ArrayList<>();
        for (int i = 0; i < 99999999; i++) {
            int n = random.nextInt(3) + 1;
            if (n == 2) {
                n = 1;
            } else if (n == 3) {
                n = 2;
            }
            integers.add(n);
        }
        int n = 0;//设置计数器
        for (int i = 0; i < integers.size(); i++) {
            if (integers.get(i) == 1) {
                n = n + 1;
            }
            if (integers.get(i) == 2) {
                n=0;
            }
            if (n == 3) {
                n = 0;
                integers.set(i, 2);
            }
        }
        double m = 0;
        for (int i : integers) {
            if (i == 2) {
                m = m + 1;
            }
        }
        System.out.println(m/integers.size());
    }
}

实验过程

通过随机生成1到3数字，用来模拟33.333%的暴击率。

将2全部改为1，3改为2，用1代表不暴击，用2代表暴击。
将其放入ArrayList集合中，然后遍历集合。

设置一个计数器初始值为0，如果遍历到的数为1则计数器+1，

如果遍历到的数字为2，则对计数器清零

如果计数器为3，则代表连续3次不暴击，将此时遍历到的数据改为2（3次必定暴击）
再次遍历集合，记录2出现的次数，并除以元素的数量求出暴击率

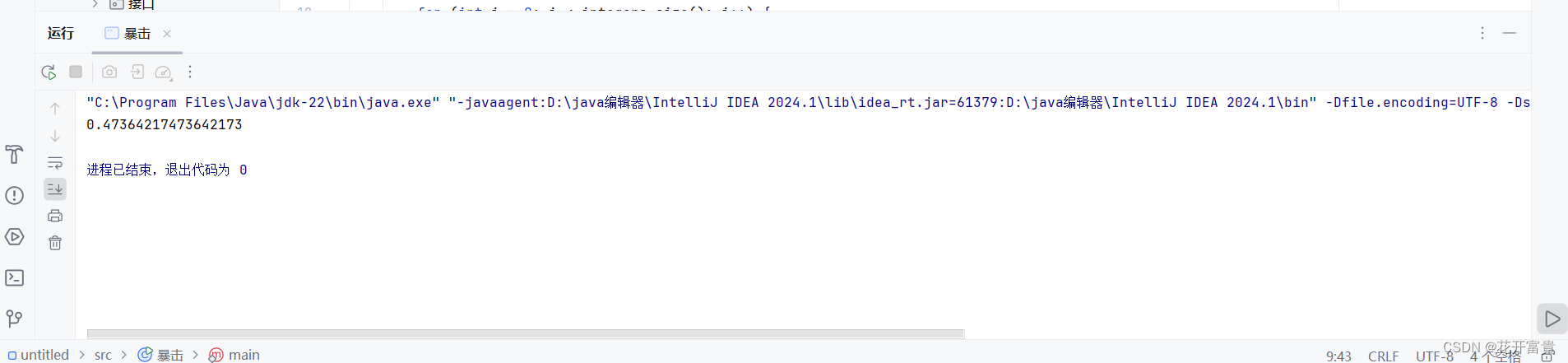
与视频作者结论一致