文章目录
- 1概率视角再了解CBOW模型
- 2另一种word2vec模型
-
- [2.1 skip-gram模型的概率表达](#2.1 skip-gram模型的概率表达)
- 3两种模型比较
1概率视角再了解CBOW模型
目的是从概率视角了解CBOW模型的训练目标;
-
CBOW模型是在给定某个上下文时,输出目标词的概率;
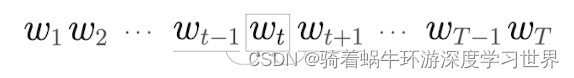
-
对于包含 w 1 , w 2 , . . . , w T w_1,w_2,...,w_T w1,w2,...,wT的语料库,CBOW模型就是在给定上下文的情况下(假设上下文窗口为1)预测目标词发生的概率,因此可以用条件概率建模:
P ( w t ∣ w t − 1 , w t + 1 ) P(w_t|w_{t-1},w_{t+1}) P(wt∣wt−1,wt+1)即在 w t − 1 w_{t-1} wt−1和 w t + 1 w_{t+1} wt+1发生后, w t w_t wt发生的概率。
-
在前面的笔记中,我们知道CBOW模型使用了交叉熵损失;对于某条数据而言,通过模型计算得到输出并转化为概率形式,记为 y y y;其真实的监督标签为 t t t;通过前面的学习我们知道,这条数据的交叉熵损失计算如下式所示:
L = − ∑ k t k log y k L=-\sum_kt_k\log y_k L=−k∑tklogyk- 注意:这里的监督标签是独热编码形式;
- 那么实际上只有 t t t中元素值为1的那个位置对应的概率才被计入了损失当中,即目标词 w t w_t wt的那个位置;
-
因此,上述交叉熵损失公式可以用条件概率来表示,即:
L = − log P ( w t ∣ w t − 1 , w t + 1 ) L=-\log P(w_t|w_{t-1},w_{t+1}) L=−logP(wt∣wt−1,wt+1) -
这还只是一条数据的交叉熵损失结果;语料库中有好多句子,每个句子都可以根据上下文大小和目标词形成训练集;
-
因此扩展到整个语料库中,就是将所有的数据的损失累加,并求均值,即:
L = − 1 T ∑ t = 1 T log P ( w t ∣ w t − 1 , w t + 1 ) L=-\frac1T\sum_{t=1}^T\log P(w_t|w_{t-1},w_{t+1}) L=−T1t=1∑TlogP(wt∣wt−1,wt+1)
2另一种word2vec模型
word2vec 有两个模型:CBOW模型和skip-gram模型
-
输入和目标的差别;如下图所示;
- CBOW模型:根据上下文单词预测中间的单词;
- skip-gram模型:根据中间的单词预测上下文是什么;

-
因此,skip-gram模型的网络结构正好相反:
-
输入层只有一个
-
输出层有多个;取决于上下文窗口的大小;下图为上下文大小为
1的情形; -
因此,首先求各个输出层的损失,然后加起来作为整个模型的损失;

-
2.1 skip-gram模型的概率表达
-
由于是根据中间的单词预测其上下文,因此目标可以建模为:
P ( w t − 1 , w t + 1 ∣ w t ) P(w_{t-1},w_{t+1}|w_t) P(wt−1,wt+1∣wt)理解为 w t w_t wt发生情况下 w t − 1 , w t + 1 w_{t-1},w_{t+1} wt−1,wt+1同时发生的概率。
-
假设上下文单词出现的概率是互相独立的,则两个单词同时出现的概率等于各自出现概率的乘积,即:
P ( w t − 1 , w t + 1 ∣ w t ) = P ( w t − 1 ∣ w t ) P ( w t + 1 ∣ w t ) P(w_{t-1},w_{t+1}|w_t)=P(w_{t-1}|w_t)P(w_{t+1}|w_t) P(wt−1,wt+1∣wt)=P(wt−1∣wt)P(wt+1∣wt) -
类比CBOW模型中使用概率来表示交叉熵损失的公式的过程:由于这里要预测的是一个上下文,我们可以把上下文看成一个整体,这个整体具有一个可取的范围;因此同样可以写成独热编码形式;那么同样的,只有 w t − 1 , w t + 1 w_{t-1},w_{t+1} wt−1,wt+1对应的独热编码中的那个位置元素值为1,其余均为0;
-
因此skip-gram模型的交叉熵损失公式也可以用下式来表示:
L = − log P ( w t − 1 , w t + 1 ∣ w t ) = − log P ( w t − 1 ∣ w t ) P ( w t + 1 ∣ w t ) = − ( log P ( w t − 1 ∣ w t ) + log P ( w t + 1 ∣ w t ) ) \begin{aligned} L& =-\log P(w_{t-1},w_{t+1}|w_t) \\ &=-\log P(w_{t-1}|w_t)P(w_{t+1}|w_t) \\ &=-(\log P(w_{t-1}|w_t)+\log P(w_{t+1}|w_t)) \end{aligned} L=−logP(wt−1,wt+1∣wt)=−logP(wt−1∣wt)P(wt+1∣wt)=−(logP(wt−1∣wt)+logP(wt+1∣wt)) -
这也证明skip-gram模型的损失是上下文各个单词损失的和;、
-
扩展到整个样本中,则有下式:
L = − 1 T ∑ t = 1 T ( log P ( w t − 1 ∣ w t ) + log P ( w t + 1 ∣ w t ) ) \begin{aligned}L=-\frac{1}{T}\sum_{t=1}^T(\log P(w_{t-1}|w_t)+\log P(w_{t+1}|w_t))\end{aligned} L=−T1t=1∑T(logP(wt−1∣wt)+logP(wt+1∣wt))
3两种模型比较
- skip-gram模型要预测的内容更多,因此,从单词的分布式表示的准确度来看, 在大多数情况下,skip-gram模型的结果更好;尤其在低频词和类推问题的性能方面。
- 但是由于skip-gram模型预测的内容多,因此学习速度慢;