浮点数计算在我们大多数项目中并没有使用到特别的科学计算部分,所以float基本都够用。double也同样有精度问题,无论怎么样都是无法避免精度导致的在逻辑中的不一致的问题。
根据 IEEE 754 标准,任意一个二进制浮点数 F 均可表示为:
F = (-1 ^ s) * (1.M) * (2 ^ e)
- s:符号位, 0/1
- M:尾数部分,具体的小数用二进制表示
- e:比例因子的指数,浮点数的指数
float
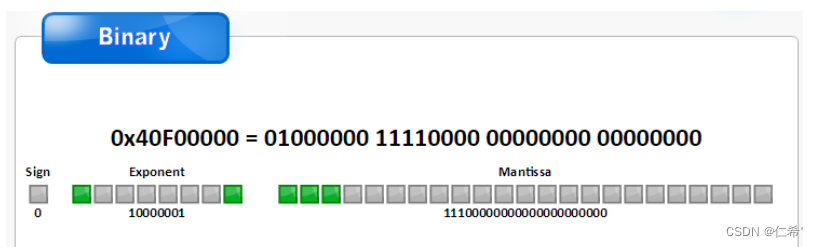
| 名称 | 长度 | 比特位置 |
|---|---|---|
| 符号位Sign(S) | 1bit | (b31) |
| 指数部分Exponent(E) | 8bit | (b30-b23) |
| 尾数部分Mantissa(M) | 23bit | (b22-b0) |
double

| 名称 | 长度 | 比特位置 |
|---|---|---|
| 符号位Sign (S) | 1bit | (b63) |
| 指数部分Exponent(E) | 11bit | (b62-b52) |
| 尾数部分Mantissa(M) | 52bit | (b51-b0) |
其中E的阶符采用隐含方式,即采用移码(补码)方法来表示正负指数。例如float的8位价码,应将指数e加上一个固定的偏移值127(01111111),即 e 加上 127才是存储在二进制中的数据。
尾数M只表示1后面的小数部分,而且是二进制直译的那种,然后再根据阶码来平移小数点。
例:9.625 => 1001.101 => 1.001101×(2^3) => 00110100000000000000000 去掉了小数点左侧的 1,并用 0 在右侧补齐。
整数部分采用 "除2取余法",小数部分则采用 "乘2取整法"。
浮点数的精度问题
例:198903.19
110000100011110111.0011000010100011(截取 16 位小数)
198903.19(10) = (-1 ^ 0) * 1.100001000111101110011000010100011 * (2 ^ 17)
小数部分 0.19 转为二进制后,小数位数超过 16 位(已经手算到小数点后 32 位都还没算完,其实这个位数是无穷尽的),因此这里导致浮点数有诸多精度的问题,它很多时候无法准确的表示数字,甚至非常不准确。
精度问题
浮点数的精度问题不只是小数点的精度问题 ,随着数值越来越大,即使是整数也开始会有相同的问题 ,因为浮点数本身是一个 1.M * (2 ^ e) 公式形式得到的数字,当数字放大时,M的尾数的存储位数没有变化,能表达的位数有限,自然越来越难以准确表达,特别是数字的末尾部分越来越难以准确表达。
常见问题
- 数值比较不相等
- 数值计算不确定,比如1f / (1f /5555f * 11110f) 结果有可能是0.4999999999991
- 不同设备计算结果不同,不同平台上的浮点数计算也有所偏差
解决方案
- 只计算一次,认定这个值为准确值,只用这个变量结果做判断,也省去了多次计算浪费的CPU
- 改用int或long型来替代浮点数
- 用定点数保持一致性并缩小精度问题 。定点数把整数部分和小数部分拆分开来,都用整数的形式表示。缺点是由于拆分了整数和小数,两个部分都要占用空间,所以受到存储位数的限制。用定点数来做计算能保证在各设备上的计算结果一致性。
- 最耗的办法,用字符串替代浮点数。
- 最差的办法,提高期望值。
C# decimal
它的内部实现就是定点数的实现方式,我们完全可以把它看作定点数来操作。
它占用128位的存储空间即一个decimal变量占用16个字节。
它的数值范围在 ±1.0 × 10^28 到 ±7.9 × 10^28之间,这么大的的占用空间却比float的取值范围还小。
decimal 精度比较大,精度范围在 28 个有效位,另外任何与它一起计算的数值都必须先转化 为 decimal 类型否则就会编译报错,数值不会隐式的自动转换成 decimal。
精度过大导致CPU 计算消耗量大,大量使用时会使得堆栈内存直线飙升,这也间接的增大了CPU的消耗。
大部分项目自己实现定点数。