【数学建模】—【Python库】—【Numpy】—【学习】

编辑

[1. NumPy安装](#1. NumPy安装)

[2. ndarray对象](#2. ndarray对象)

[1. 创建ndarray](#1. 创建ndarray)

1.从列表或元组创建：

2.使用内置函数创建：

[2. ndarray属性](#2. ndarray属性)

[3. 数组运算](#3. 数组运算)

[1. 基本运算](#1. 基本运算)

[2. 数学函数](#2. 数学函数)

3.统计函数

[4. 数组索引与切片](#4. 数组索引与切片)

[1. 一维数组索引与切片](#1. 一维数组索引与切片)

2.多维数组索引与切片

[5. 数组形状操作](#5. 数组形状操作)

[1. 改变数组形状](#1. 改变数组形状)

[2. 数组转置](#2. 数组转置)

[6. 数组拼接与分割](#6. 数组拼接与分割)

[1. 数组拼接](#1. 数组拼接)

[2. 数组分割](#2. 数组分割)

[7. 广播机制](#7. 广播机制)

[8. 常用函数](#8. 常用函数)

[1. 数组生成函数](#1. 数组生成函数)

2.数学运算函数

[9. 高级运算](#9. 高级运算)

[1. 矩阵运算](#1. 矩阵运算)

2.统计运算

[10. 实践案例](#10. 实践案例)

[1. 数据分析案例](#1. 数据分析案例)

[2. 数值计算案例](#2. 数值计算案例)

[11. NumPy与其他库的结合](#11. NumPy与其他库的结合)

[12. NumPy高级功能](#12. NumPy高级功能)

[1. 线性代数](#1. 线性代数)

[2. 随机数生成](#2. 随机数生成)

[3. FFT（快速傅里叶变换）](#3. FFT（快速傅里叶变换）)

[13. NumPy性能优化](#13. NumPy性能优化)

[1. 向量化操作](#1. 向量化操作)

[2. 避免不必要的复制](#2. 避免不必要的复制)

[编辑14. 总结](#编辑14. 总结)

NumPy综合总结

[1. 简介](#1. 简介)

[2. 安装与导入](#2. 安装与导入)

[3. ndarray对象](#3. ndarray对象)

[4. 数组运算](#4. 数组运算)

[5. 数组索引与切片](#5. 数组索引与切片)

[6. 数组形状操作](#6. 数组形状操作)

[7. 数组拼接与分割](#7. 数组拼接与分割)

[8. 广播机制](#8. 广播机制)

[9. 常用函数](#9. 常用函数)

[10. 高级运算](#10. 高级运算)

[11. 实践案例](#11. 实践案例)

[12. NumPy与其他库的结合](#12. NumPy与其他库的结合)

[13. NumPy高级功能](#13. NumPy高级功能)

[14. NumPy性能优化](#14. NumPy性能优化)

结论

专栏：数学建模学习笔记

pycharm专业版免费激活教程见资源

python相关库的安装：pandas,numpy,matplotlib，statsmodels

总篇：【数学建模】---【新手小白到国奖选手】---【学习路线】

本篇属于第一卷------Numpy学习笔记

NumPy（Numerical Python）是Python编程语言的一个库，支持大规模的多维数组与矩阵运算，此外还提供了大量的数学函数库。NumPy在科学计算和数据分析领域有着广泛的应用。其核心是一个高效的多维数组对象，称为ndarray。

1. NumPy安装

要使用NumPy库，首先需要安装它。可以通过pip来安装：

pip install numpy

安装完成后，可以通过以下方式导入NumPy库：

import numpy as np

2. ndarray对象

NumPy的核心是ndarray对象，它是一个多维数组。它和Python的列表类似，但提供了更高效的存储和运算功能。

1. 创建ndarray

可以通过多种方式创建ndarray对象：

1.从列表或元组创建：

import numpy as np

# 从列表创建
a = np.array([1, 2, 3])
print(a)  # 输出：[1 2 3]

# 从嵌套列表创建
b = np.array([[1, 2, 3], [4, 5, 6]])
print(b)  # 输出：
# [[1 2 3]
#  [4 5 6]]

2.使用内置函数创建：

import numpy as np

# 创建全零数组
zeros_array = np.zeros((2, 3))
print(zeros_array)  # 输出：
# [[0. 0. 0.]
#  [0. 0. 0.]]

# 创建全一数组
ones_array = np.ones((2, 3))
print(ones_array)  # 输出：
# [[1. 1. 1.]
#  [1. 1. 1.]]

# 创建一个值为5的数组
full_array = np.full((2, 3), 5)
print(full_array)  # 输出：
# [[5 5 5]
#  [5 5 5]]

# 创建单位矩阵
eye_array = np.eye(3)
print(eye_array)  # 输出：
# [[1. 0. 0.]
#  [0. 1. 0.]
#  [0. 0. 1.]]

# 创建随机数组
random_array = np.random.random((2, 3))
print(random_array)  # 输出（示例）：
#[[0.55827818 0.41537687 0.41252448]
# [0.10251325 0.7435904  0.69922825]]

2. ndarray属性

ndarray对象有许多属性，用于描述数组的形状、维度、数据类型等：

import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])

print("数组维度：", a.ndim)  # 输出：数组维度： 2
print("数组形状：", a.shape)  # 输出：数组形状： (2, 3)
print("数组大小：", a.size)  # 输出：数组大小： 6
print("数组数据类型：", a.dtype)  # 输出：数组数据类型： int32
print("数组元素大小：", a.itemsize)  # 输出：数组元素大小： 4
print("数组数据缓冲区：", a.data)  # 输出：数组数据缓冲区： <memory at 0x000001F49D4336B0>

3. 数组运算

NumPy提供了丰富的数组运算功能，可以对ndarray对象进行数学运算、逻辑运算、统计运算等。

1. 基本运算

可以对数组进行元素级别的运算：

import numpy as np

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])

# 加法
print(a + b)  # 输出：[5 7 9]

# 减法
print(a - b)  # 输出：[-3 -3 -3]

# 乘法
print(a * b)  # 输出：[ 4 10 18]

# 除法
print(a / b)  # 输出：[0.25 0.4  0.5 ]

2. 数学函数

NumPy提供了大量的数学函数，可以对数组进行逐元素的计算：

import numpy as np

a = np.array([0, np.pi / 2, np.pi])

# 三角函数
print(np.sin(a))  # 输出：[0.000000e+00 1.000000e+00 1.224647e-16]
print(np.cos(a))  # 输出：[ 1.000000e+00  6.123234e-17 -1.000000e+00]
print(np.tan(a))  # 输出：[ 0.00000000e+00  1.63312394e+16 -1.22464680e-16]

# 指数和对数
print(np.exp(a))  # 输出：[ 1.          4.48168907 23.14069263]
print(np.log(a))  # 输出：[-inf  0.         1.14472989]（注：0的对数为负无穷）
print(np.log10(a))  # 输出：[-inf  0.          0.49714987]（注：0的对数为负无穷）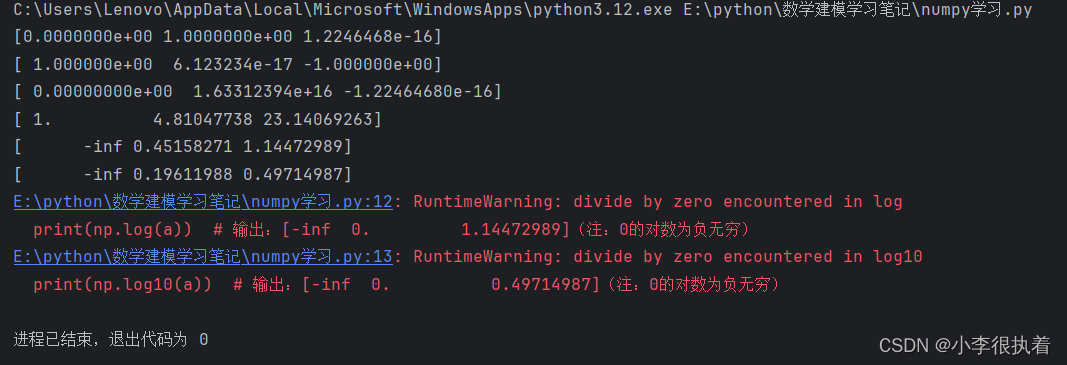

在使用NumPy计算数组中元素的对数时，当数组中包含零元素时，会出现"divide by zero encountered in log"或"divide by zero encountered in log10"这样的警告。这是因为对数函数在零值处无定义，对数为负无穷（-inf）。

这些警告是由零值引起的，它们在对数运算中会导致无穷大的结果。这在NumPy中是一个正常的行为，提醒你注意输入数据中的零值。

如果你想避免这些警告，可以在计算对数之前，处理数组中的零值。你可以将零值替换为一个非常小的正数，例如 np.finfo(float).eps（浮点数的最小可表示正数），以避免这些警告。以下是一个示例代码：确保在替换零值之前，数组已经正确更新。

import numpy as np

a = np.array([0, 1, 3])
# 替换数组中的零值为非常小的正数
a = np.where(a == 0, np.finfo(float).eps, a)

print(np.log(a))    # 输出不会包含负无穷
print(np.log10(a))  # 输出不会包含负无穷

确保代码执行顺序正确，即先替换零值再计算对数。这段代码首先将数组 a 中的零值替换为 np.finfo(float).eps，然后计算 a 的自然对数和常用对数，这样就不会再出现除以零的警告了。

3.统计函数

NumPy提供了多种统计函数，可以对数组进行统计运算：

import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])

# 最小值
print(np.min(a))  # 输出：1

# 最大值
print(np.max(a))  # 输出：6

# 和
print(np.sum(a))  # 输出：21

# 均值
print(np.mean(a))  # 输出：3.5

# 标准差
print(np.std(a))  # 输出：1.707825127659933

# 中位数
print(np.median(a))  # 输出：3.5

# 累积和
print(np.cumsum(a))  # 输出：[ 1  3  6 10 15 21]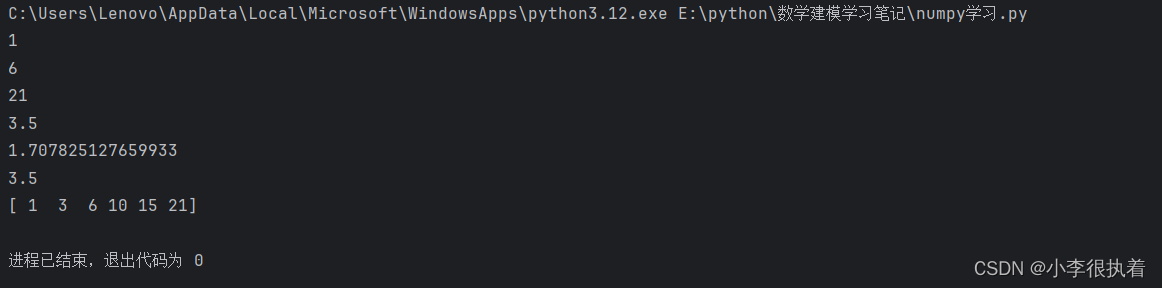

4. 数组索引与切片

NumPy提供了强大的数组索引与切片功能，可以方便地访问和修改数组元素。

1. 一维数组索引与切片

import numpy as np

a = np.array([0, 1, 2, 3, 4, 5])

# 索引
print(a[0])  # 输出：0  输出第一个元素
print(a[-1])  # 输出：5  输出最后一个元素

# 切片
print(a[1:3])  # 输出：[1 2]  输出第二个到第三个元素
print(a[:3])  # 输出：[0 1 2]  输出前三个元素
print(a[3:])  # 输出：[3 4 5]  输出第三个到最后一个元素
print(a[::2])  # 输出：[0 2 4]  每隔一个元素输出一个元素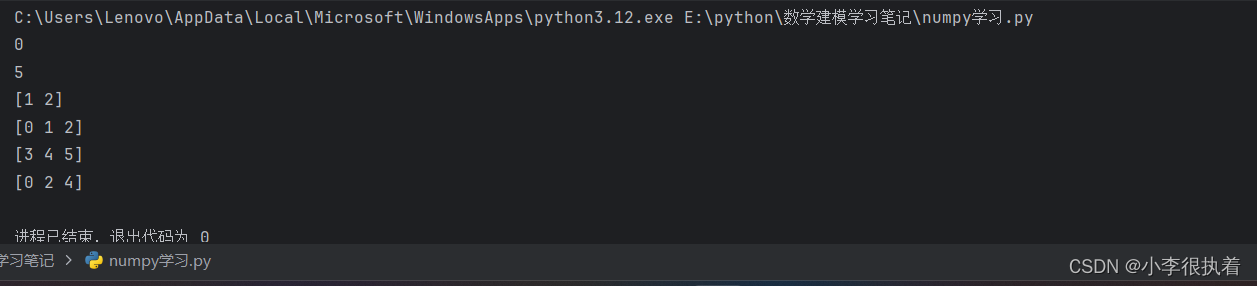

2.多维数组索引与切片

import numpy as np

a = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8]])

# 索引
print(a[0, 0])  # 输出：0  输出第一行第一列的元素
print(a[1, -1])  # 输出：5  输出第二行最后一个元素

# 切片
print(a[:2, 1:3])  # 输出：
# [[1 2]
#  [4 5]]  输出第一行到第二行，第二列到第三列的元素

print(a[::2, ::2])  # 输出：
# [[0 2]
#  [6 8]]  每隔一行一列输出一个元素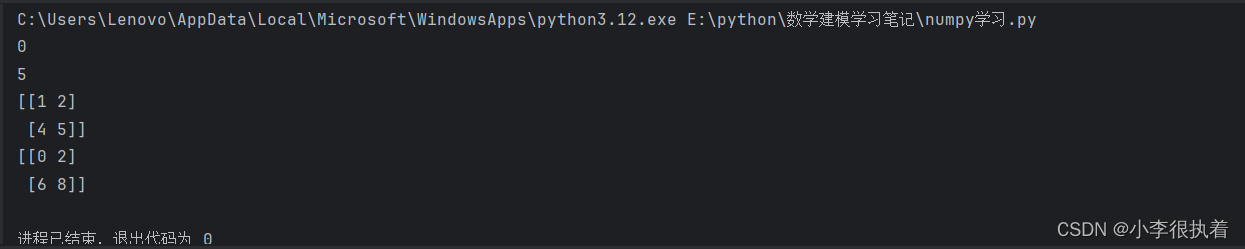

5. 数组形状操作

NumPy提供了多种函数来改变数组的形状。

1. 改变数组形状

import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])

# 改变形状
print(a.reshape(3, 2))  # 输出：
# [[1 2]
#  [3 4]
#  [5 6]]

print(a.flatten())  # 将数组展平成一维  输出：[1 2 3 4 5 6]

2. 数组转置

import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])

# 转置
print(a.T)  # 输出：
# [[1 4]
#  [2 5]
#  [3 6]]

6. 数组拼接与分割

NumPy提供了拼接与分割数组的函数。

1. 数组拼接

import numpy as np

a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6]])

# 垂直拼接
print(np.vstack((a, b)))  # 输出：
# [[1 2]
#  [3 4]
#  [5 6]]

# 水平拼接
print(np.hstack((a, b.T)))  # 输出：
# [[1 2 5]
#  [3 4 6]]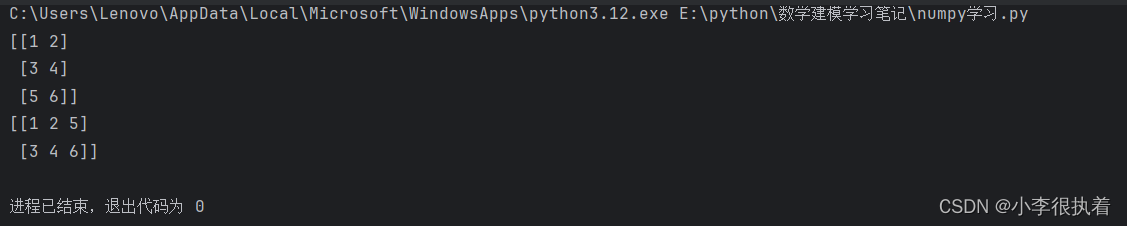

2. 数组分割

import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])

# 水平分割
print(np.hsplit(a, 3))  # 输出：[array([[1], [4]]), array([[2], [5]]), array([[3], [6]])]

# 垂直分割
print(np.vsplit(a, 2))  # 输出：[array([[1, 2, 3]]), array([[4, 5, 6]])]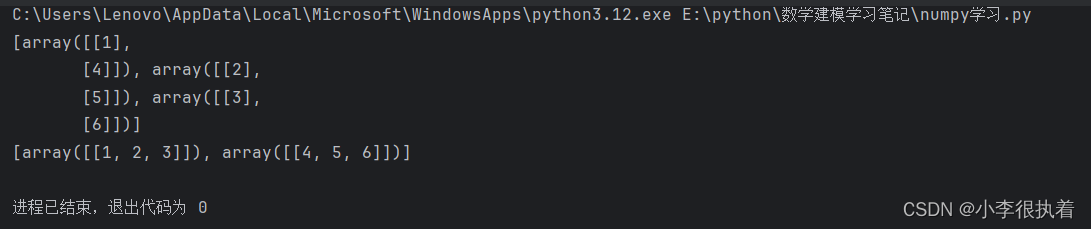

7. 广播机制

NumPy的广播机制允许不同形状的数组进行算术运算。广播的规则是：

如果数组的维度不同，将维度较小的数组进行扩展，直到两个数组的维度相同。
如果两个数组在某个维度上的长度不同，但其中一个长度为1，则可以进行运算。
如果两个数组在任何一个维度上的长度都不相同且都不为1，则无法进行广播。

import numpy as np

a = np.array([1, 2, 3])
b = np.array([[0], [1], [2]])

广播机制

print(a + b) # 输出：

[[1 2 3]

[2 3 4]

[3 4 5]]

8. 常用函数

NumPy提供了许多常用函数，以下列出一些常用函数的示例。

1. 数组生成函数

import numpy as np

# 创建全零数组
print(np.zeros((2, 3)))  # 输出：
# [[0. 0. 0.]
#  [0. 0. 0.]]

# 创建全一数组
print(np.ones((2, 3)))  # 输出：
# [[1. 1. 1.]
#  [1. 1. 1.]]

# 创建指定值数组
print(np.full((2, 3), 5))  # 输出：
# [[5 5 5]
#  [5 5 5]]

# 创建单位矩阵
print(np.eye(3))  # 输出：
# [[1. 0. 0.]
#  [0. 1. 0.]
#  [0. 0. 1.]]

# 创建随机数组
print(np.random.random((2, 3)))  # 输出（示例）：
# [[0.97601061 0.54150051 0.71578887]
 #[0.44954629 0.74204514 0.63492767]]

# 创建等差数组
print(np.arange(0, 10, 2))  # 输出：[0 2 4 6 8]

# 创建等比数组
print(np.linspace(0, 1, 5))  # 输出：[0.   0.25 0.5  0.75 1.  ]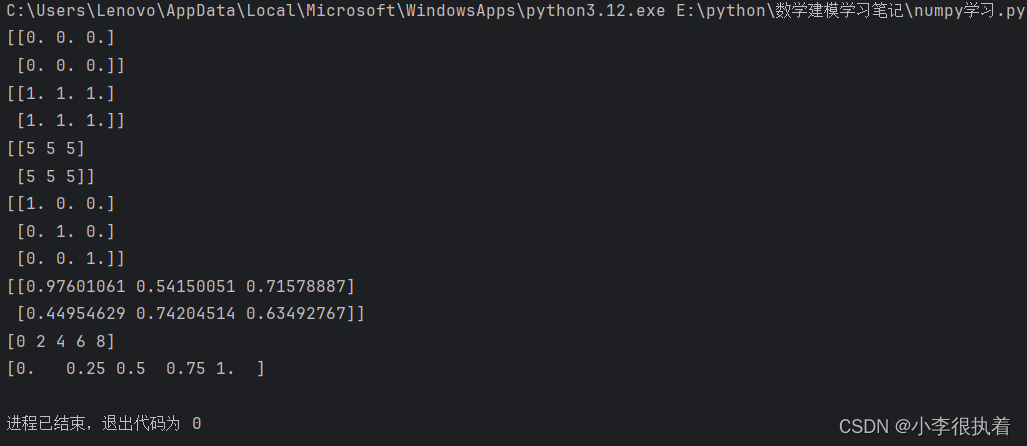

2.数学运算函数

import numpy as np

a = np.array([1, 2, 3, 4])

# 求和
print(np.sum(a))  # 输出：10

# 求乘积
print(np.prod(a))  # 输出：24

# 求累积和
print(np.cumsum(a))  # 输出：[ 1  3  6 10]

# 求累积乘积
print(np.cumprod(a))  # 输出：[ 1  2  6 24]

9. 高级运算

1. 矩阵运算

NumPy提供了丰富的矩阵运算函数。

import numpy as np

a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])

# 矩阵乘法
print(np.dot(a, b))  # 输出：
# [[19 22]
#  [43 50]]

# 矩阵行列式
print(np.linalg.det(a))  # 输出：-2.0000000000000004

# 矩阵逆
print(np.linalg.inv(a))  # 输出：
# [[-2.   1. ]
#  [ 1.5 -0.5]]

# 矩阵特征值
print(np.linalg.eig(a))  # 输出：（特征值，特征向量）
# EigResult(eigenvalues=array([-0.37228132,  5.37228132]), #eigenvectors=array([[-0.82456484, -0.41597356],
 #      [ 0.56576746, -0.90937671]]))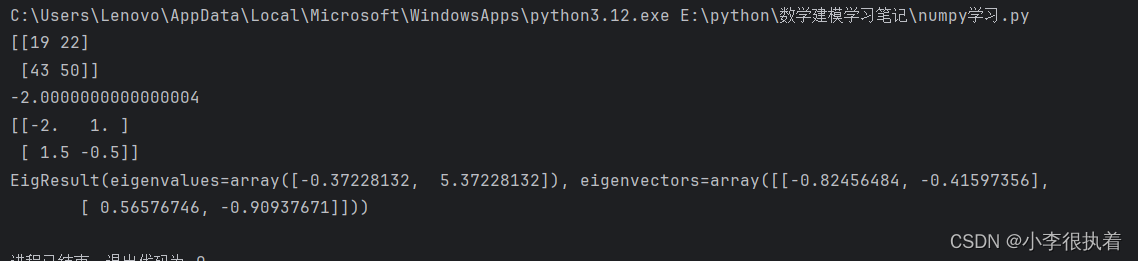

2.统计运算

NumPy提供了多种统计运算函数。

import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])

# 均值
print(np.mean(a))  # 输出：3.5

# 中位数
print(np.median(a))  # 输出：3.5

# 方差
print(np.var(a))  # 输出：2.9166666666666665

# 标准差
print(np.std(a))  # 输出：1.707825127659933

# 最小值
print(np.min(a))  # 输出：1

# 最大值
print(np.max(a))  # 输出：6

# 百分位数
print(np.percentile(a, 50))  # 输出：3.5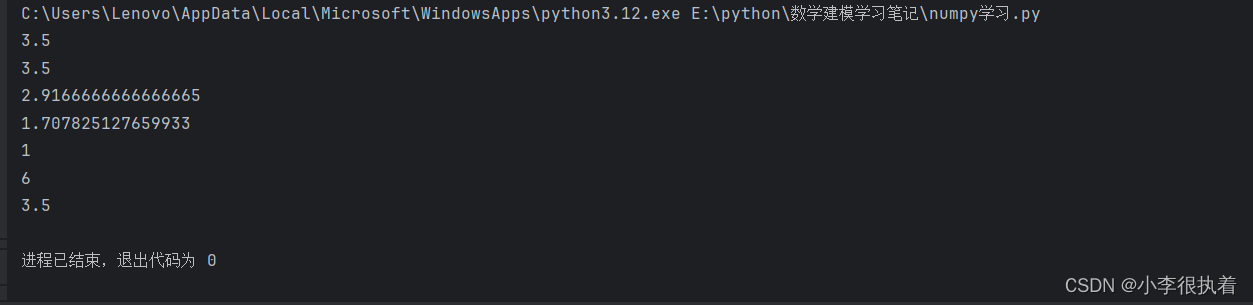

10. 实践案例

1. 数据分析案例

以下是一个简单的数据分析案例，展示如何使用NumPy进行数据处理和分析。

import numpy as np

# 生成模拟数据
data = np.random.randn(1000)

# 计算均值和标准差
mean = np.mean(data)
std_dev = np.std(data)

print(f"均值: {mean}, 标准差: {std_dev}")  # 示例输出：均值: -0.015971063944354425, 标准差: 0.9670869531250885
# 计算数据的直方图
hist, bin_edges = np.histogram(data, bins=10)
print(hist)  # 示例输出：[  4   8  53 101 227 251 204 111  34   7]
print(bin_edges)  # 示例输出：[-3.42803477 -2.79654529 -2.16505581 -1.53356634 -0.90207686 -0.27058738
#  0.36090209  0.99239157  1.62388104  2.25537052  2.88686   ]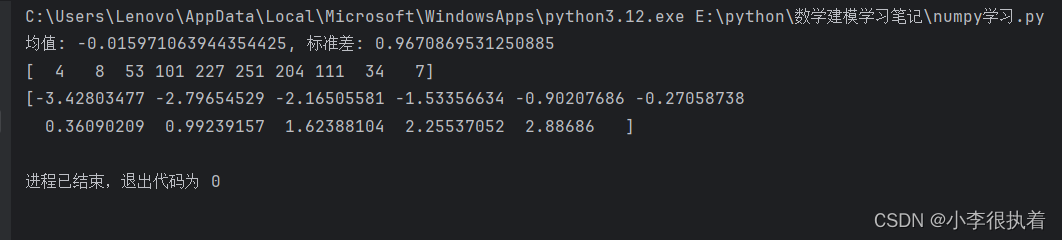

2. 数值计算案例

以下是一个简单的数值计算案例，展示如何使用NumPy进行数值计算。

import numpy as np

# 定义函数
def f(x):
    return x**2 - 4*x + 4

# 生成数据
x = np.linspace(-10, 10, 100)

# 计算函数值
y = f(x)

print(y)  
"""
示例输出：
[1.44000000e+02 1.39192327e+02 1.34466279e+02 1.29821855e+02
 1.25259055e+02 1.20777880e+02 1.16378329e+02 1.12060402e+02
 1.07824100e+02 1.03669421e+02 9.95963677e+01 9.56049383e+01
 9.16951331e+01 8.78669524e+01 8.41203959e+01 8.04554637e+01
 7.68721559e+01 7.33704724e+01 6.99504132e+01 6.66119784e+01
 6.33551678e+01 6.01799816e+01 5.70864198e+01 5.40744822e+01
 5.11441690e+01 4.82954801e+01 4.55284155e+01 4.28429752e+01
 4.02391593e+01 3.77169677e+01 3.52764004e+01 3.29174574e+01
 3.06401388e+01 2.84444444e+01 2.63303745e+01 2.42979288e+01
 2.23471074e+01 2.04779104e+01 1.86903377e+01 1.69843893e+01
 1.53600653e+01 1.38173656e+01 1.23562902e+01 1.09768391e+01
 9.67901235e+00 8.46280992e+00 7.32823181e+00 6.27527803e+00
 5.30394858e+00 4.41424344e+00 3.60616264e+00 2.87970615e+00
 2.23487399e+00 1.67166616e+00 1.19008264e+00 7.90123457e-01
 4.71788593e-01 2.35078053e-01 7.99918376e-02 6.52994592e-03
 1.46923783e-02 1.04479135e-01 2.75890215e-01 5.28925620e-01
 8.63585348e-01 1.27986940e+00 1.77777778e+00 2.35731048e+00
 3.01846750e+00 3.76124885e+00 4.58565453e+00 5.49168452e+00
 6.47933884e+00 7.54861749e+00 8.69952046e+00 9.93204775e+00
 1.12461994e+01 1.26419753e+01 1.41193756e+01 1.56784002e+01
 1.73190491e+01 1.90413223e+01 2.08452199e+01 2.27307418e+01
 2.46978880e+01 2.67466585e+01 2.88770534e+01 3.10890725e+01
 3.33827160e+01 3.57579839e+01 3.82148760e+01 4.07533925e+01
 4.33735333e+01 4.60752984e+01 4.88586879e+01 5.17237017e+01
 5.46703398e+01 5.76986022e+01 6.08084889e+01 6.40000000e+01]
"""

11. NumPy与其他库的结合

NumPy通常与其他库结合使用，如Pandas、Matplotlib、SciPy等。以下是一个简单的示例，展示如何结合NumPy和Matplotlib进行数据可视化。

import numpy as np
import matplotlib.pyplot as plt

# 生成数据
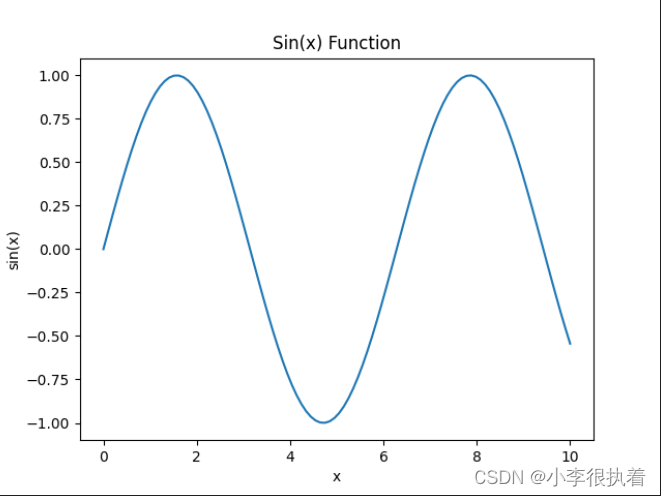
x = np.linspace(0, 10, 100)
y = np.sin(x)

# 绘制数据
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('sin(x)')
plt.title('Sin(x) Function')
plt.show()

运行结果：一幅展示sin(x)函数的折线图，其中x轴表示从0到10的均匀分布的数据，y轴表示sin(x)的值。

12. NumPy高级功能

1. 线性代数

NumPy提供了丰富的线性代数功能，可以进行矩阵乘法、矩阵分解、特征值计算等。

import numpy as np

a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])

# 矩阵乘法
print(np.dot(a, b))  # 输出：
# [[19 22]
#  [43 50]]

# 矩阵行列式
print(np.linalg.det(a))  # 输出：-2.0000000000000004

# 矩阵逆
print(np.linalg.inv(a))  # 输出：
# [[-2.   1. ]
#  [ 1.5 -0.5]]

# 矩阵特征值
print(np.linalg.eig(a))  # 输出：（特征值，特征向量）
# (array([-0.37228132,  5.37228132]), 
#  array([[-0.82456484, -0.41597356],
#         [ 0.56576746, -0.90937671]]))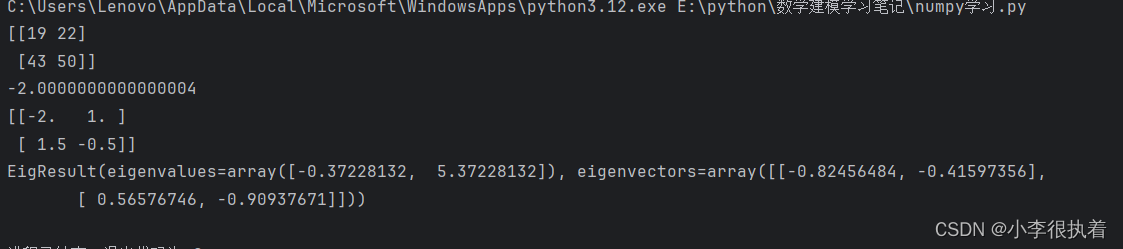

2. 随机数生成

NumPy提供了丰富的随机数生成功能，可以生成各种分布的随机数。

import numpy as np

# 生成均匀分布的随机数
print(np.random.rand(2, 3))  # 输出（示例）：
# [[0.2177449  0.71579651 0.40282945]
#  [0.00823481 0.2378211  0.22714768]]

# 生成标准正态分布的随机数
print(np.random.randn(2, 3))  # 输出（示例）：
# [[-0.02638322 -0.29821612 -0.57163728]
#  [ 0.023793   -0.03624107  0.5007041 ]]

# 生成指定区间的随机整数
print(np.random.randint(0, 10, size=(2, 3)))  # 输出（示例）：
# [[9 0 6]
#  [4 5 5]]
# 生成指定分布的随机数
print(np.random.normal(loc=0, scale=1, size=(2, 3)))  # 输出（示例）：
#[[-0.05426652  0.00228263 -0.27759785]
 #[-0.47845462  2.04304079 -0.84451445]]

3. FFT（快速傅里叶变换）

NumPy提供了快速傅里叶变换功能，可以对数组进行快速傅里叶变换。

import numpy as np

a = np.array([0, 1, 2, 3])

# 快速傅里叶变换
print(np.fft.fft(a))  # 输出：
# [ 6.+0.j -2.+2.j -2.+0.j -2.-2.j]

# 逆快速傅里叶变换
print(np.fft.ifft(a))  # 输出：
# [ 1.5+0.j -0.5+0.5j -0.5+0.j -0.5-0.5j]

13. NumPy性能优化

NumPy通过其底层实现，已经大大优化了性能，但在实际应用中仍有许多技巧可以进一步提升性能。

1. 向量化操作

尽量使用向量化操作代替显式的Python循环，以提高性能。

import numpy as np

a = np.arange(1000000)

# 使用向量化操作
result = a * 2
print(result[:10])  # 输出：[ 0  2  4  6  8 10 12 14 16 18]

2. 避免不必要的复制

在操作大数组时，尽量避免不必要的数组复制操作，以减少内存使用和提高性能。

import numpy as np

a = np.arange(1000000)

# 避免不必要的复制
b = a[:500000]
print(b[:10])  # 输出：[0 1 2 3 4 5 6 7 8 9]

14. 总结

NumPy综合总结

本文通过详细的讲解和丰富的代码示例，全面介绍了NumPy库的基础知识、常用功能和高级应用，为初学者提供了深入理解和灵活使用NumPy的指南。

1. 简介

NumPy（Numerical Python）是Python编程语言的一个库，专门用于大规模的多维数组与矩阵运算。NumPy是科学计算和数据分析的重要工具，其核心是高效的多维数组对象ndarray。

2. 安装与导入

通过pip可以轻松安装NumPy库，导入方式为 import numpy as np。

3. ndarray对象

ndarray对象是NumPy的核心，可以通过列表、元组或内置函数创建。ndarray具有多种属性，如维度、形状、大小、数据类型等，方便用户对数组进行描述和操作。

4. 数组运算

NumPy提供了丰富的运算功能，包括基本运算、数学函数和统计函数。用户可以对数组进行元素级别的加减乘除运算，使用三角函数、指数和对数函数进行复杂计算，还可以进行求和、均值、标准差等统计运算。

5. 数组索引与切片

NumPy的索引与切片功能强大，可以方便地访问和修改数组元素。支持一维和多维数组的索引和切片操作，使得数据操作更加灵活。

6. 数组形状操作

NumPy提供了改变数组形状的多种函数，如reshape、flatten和转置函数，使得用户可以轻松调整数组的结构以满足不同的计算需求。

7. 数组拼接与分割

NumPy支持数组的拼接与分割操作，用户可以使用vstack和hstack进行垂直和水平拼接，使用hsplit和vsplit进行数组分割。

8. 广播机制

广播机制允许不同形状的数组进行算术运算，极大地方便了数组的操作和计算。理解广播机制的规则有助于更有效地使用NumPy进行数组运算。

9. 常用函数

NumPy提供了多种常用函数，如创建全零数组、全一数组、单位矩阵、随机数组，以及生成等差和等比数组的函数。这些函数简化了数组的生成过程。

10. 高级运算

NumPy的高级运算功能包括矩阵运算和统计运算，支持矩阵乘法、行列式、矩阵逆和特征值计算，提供了丰富的统计函数，如均值、中位数、方差和标准差等。

11. 实践案例

本文通过数据分析和数值计算的实际案例，展示了如何使用NumPy进行数据处理和分析，以及进行数值计算，帮助读者将理论知识应用于实践。

12. NumPy与其他库的结合

NumPy通常与Pandas、Matplotlib、SciPy等库结合使用。本文展示了如何结合NumPy和Matplotlib进行数据可视化，进一步扩展了NumPy的应用范围。

13. NumPy高级功能

NumPy提供了线性代数、随机数生成和快速傅里叶变换等高级功能，使得其在科学计算和工程应用中更加得心应手。

14. NumPy性能优化

通过向量化操作和避免不必要的复制，用户可以进一步优化NumPy的性能，提升代码运行效率。

结论

NumPy作为Python科学计算的基础库，提供了强大的数组处理能力和丰富的数学函数，广泛应用于数据分析、科学计算、工程应用等领域。通过本篇详细的介绍和示例，读者可以全面掌握NumPy的使用方法，并在实际项目中灵活应用，从而大幅提升计算效率和编程体验。

【数学建模】—【Python库】—【Numpy】—【学习】

1. NumPy安装

2. ndarray对象

1. 创建ndarray

1.从列表或元组创建：

2.使用内置函数创建：

2. ndarray属性

3. 数组运算

1. 基本运算

2. 数学函数

3.统计函数

4. 数组索引与切片

1. 一维数组索引与切片

2.多维数组索引与切片

5. 数组形状操作

1. 改变数组形状

2. 数组转置

6. 数组拼接与分割

1. 数组拼接

2. 数组分割

7. 广播机制

广播机制

[[1 2 3]

[2 3 4]

[3 4 5]]

8. 常用函数

1. 数组生成函数

2.数学运算函数

9. 高级运算

1. 矩阵运算

2.统计运算

10. 实践案例

1. 数据分析案例

2. 数值计算案例

11. NumPy与其他库的结合

12. NumPy高级功能

1. 线性代数

2. 随机数生成

3. FFT（快速傅里叶变换）

13. NumPy性能优化

1. 向量化操作

2. 避免不必要的复制

14. 总结

NumPy综合总结

1. 简介

2. 安装与导入

3. ndarray对象

4. 数组运算

5. 数组索引与切片

6. 数组形状操作

7. 数组拼接与分割

8. 广播机制

9. 常用函数

10. 高级运算

11. 实践案例

12. NumPy与其他库的结合

13. NumPy高级功能

14. NumPy性能优化

结论