【数据结构】树

树的基本概念

树是n(n>=0)个有限数据元素的集合。

特点：

1、树的根结点没有前驱结点，除根结点之外的所有结点有且只有一个前驱结点。

2、树中所有结点可以有0或多个后继结点。

基本术语：

结点的度：结点的分支数

终端结点（叶子）：度为0的结点

结点的层次：根结点层次为1，根结点子树的根为第2层，以此类推

树的度：树的所有结点度的最大值

树的深度：树的所有结点层次的最大值

有序树、无序树：树的每棵子树从左往右的排列有一定顺序，不得互换，为有序树，否则为无序树

森林：m(m>=0)棵互不相交的树的集合

二叉树

定义

1、每个结点最多有两颗子树

2、子树有左右之分

性质

1、在二叉树的第i层上最多有个结点(i>=1)；

2、深度为k的二叉树最多有个结点(k>=1)，深度为k的二叉树有个结点为满二叉树，

结点位置与对应满二叉树的结点一一对应为完全二叉树 （基于完全二叉树，增加一定的限制条件后即为***二叉堆***）；

3、对于任一棵二叉树BT，如果度为0的结点个数为，度为2的结点个数为，则=+1；

假设树的结点数为n，度为0的结点个数为，度为1的结点个数为，度为2的结点个数为，则有，另外树的连线个数再加上根结点也是树的总结点数，而树的连线个数为，则有，综上得=+1。

4、具有n个结点的完全二叉树的深度为, 为不大于的最大整数；

5、对于有n个结点的完全二叉树中所有结点按照从上到下、从左到右顺序进行编号，则对其中任一结点i(1<=i<=n)，都有：

i=1时，该结点是这棵树的根，没有双亲，否则双亲结点编号为[i/2]；
2*i>n时，该结点没有左孩子，否则其左孩子编号为2*i；
2*i+1>n时，该结点没有右孩子，否则其右孩子编号为2*i+1；

存储结构

1、顺序存储结构

只适用于完全二叉树，按照每个结点的编号顺序存放结点内容
空间利用率高，可以通过下标快速寻找孩子和双亲的位置

2、链式存储结构

最常用
二叉链式存储
三叉链式存储

遍历

先序遍历

根结点->先序遍历根的左子树->先序遍历根的右子树

中序遍历

中序遍历根的左子树->根结点->中序遍历根的右子树

后序遍历

后序遍历根的左子树->后序遍历根的右子树->根结点

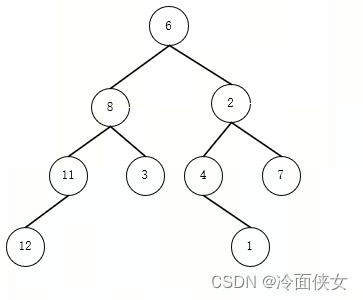
以下面的二叉树为例，它的先序遍历、中序遍历、后序遍历分别是：

6 8 11 12 3 2 4 1 7

12 11 8 3 6 4 1 2 7

12 11 3 8 1 4 7 2 6

仅通过先序遍历和后序遍历无法确定一棵树

二叉搜索树（BST)

1、非空左子树的所有键值小于其根结点的键值

2、非空右子树的所有键值大于其根结点的键值

3、左右子树都是二叉搜索树

二叉搜索树一定程度上可以提高搜索效率，但是当原序列有序时，例如序列 A = {1，2，3，4，5，6}，构造二叉搜索树如图 1.1。依据此序列构造的二叉搜索树为右斜树，同时二叉树退化成单链表，搜索效率降低为 O(n)。

二叉搜索树的查找效率取决于树的高度，当节点数目一定，保持树的左右两端保持平衡，树的查找效率最高，因此引入下面的平衡二叉搜索树。

平衡二叉搜索树（AVL树，Balanced Binary Tree （BBT）)

什么是平衡二叉树（AVL） - 知乎 (zhihu.com)

特点

1、非空左子树的所有键值小于其根结点的键值

2、非空右子树的所有键值大于其根结点的键值

3、左右子树都是二叉搜索树

4、任一结点的两个子树高度差（平衡因子BF）等于-1、0、1

结点结构：

typedef struct AVLNode *Tree;

typedef int ElementType;

struct AVLNode{

    int depth; //深度，这里计算每个结点的深度，通过深度的比较可得出是否平衡

    Tree parent; //该结点的父节点

    ElementType val; //结点值

    Tree lchild;

    Tree rchild;

    AVLNode(int val=0) {
        parent = NULL;
        depth = 0;
        lchild = rchild = NULL;
        this->val=val;
    }
};

插入

插入数据时，AVL树通过旋转最小失衡子树 来维持整棵树的平衡。在新插入的结点向上查找，以第一个平衡因子的绝对值 超过 1 的结点为根的子树称为最小失衡子树

左旋

（1）结点的右孩子替代此结点位置

（2）右孩子的左子树变为该结点的右子树

（3）结点本身变为右孩子的左子树

右旋

（1）结点的左孩子代表此结点

（2）结点的左孩子的右子树变为结点的左子树

（3）将此结点作为左孩子的右子树。

四种插入方式

在结点左孩子的左子树上插入导致失衡（LL） ->对以结点为根的树执行右旋

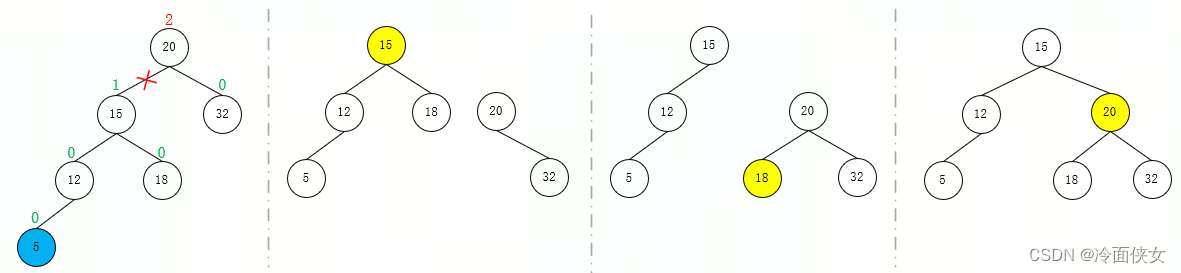
在结点右孩子的右子树上插入导致失衡（RR）->对以结点为根的树执行左旋

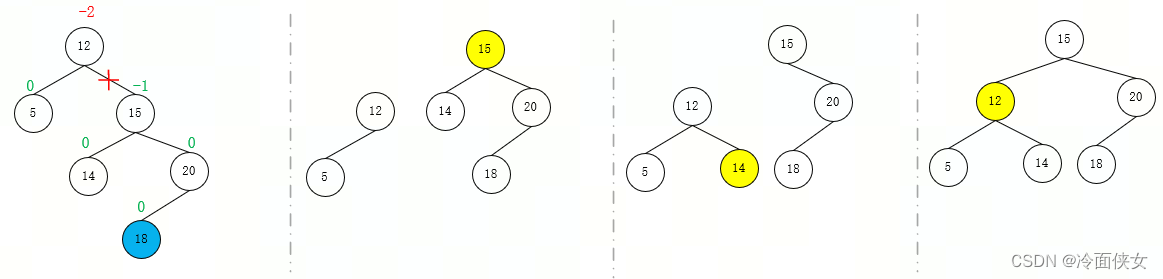
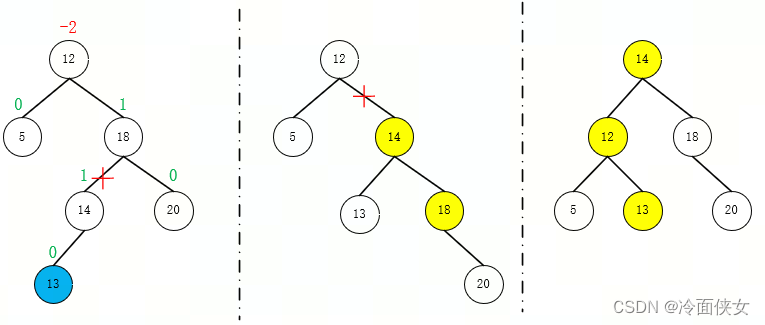
在结点左孩子的右子树上插入导致失衡（LR）->先对结点的左子树执行左旋，再对以结点为根的树执行右旋

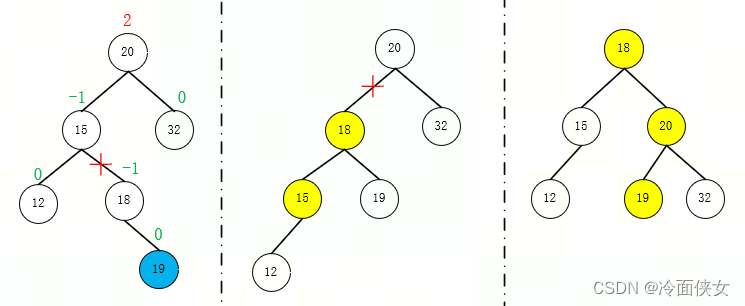
在结点右孩子的左子树上插入导致失衡（RL）->先对结点的右子树执行右旋，再对以结点为根的树执行左旋

删除

（1）删除叶子结点->直接删除，然后依次向上调整为AVL树

（2）删除的结点只有左子树->将该结点的值替换为左孩子的值，然后删除左孩子结点【根据AVL树的特性，左孩子一定是叶子节点，转化为情况（1）】

（3）删除的结点只有右子树->将该结点的值替换为右孩子的值，然后删除右孩子结点【根据AVL树的特性，右孩子一定是叶子节点，转化为情况（1）】

（4）删除的结点既有左子树又有右子树->将该结点的值替换为中序遍历的前继结点或后继结点，然后删除前继结点或后继结点【根据中序遍历的特性，前继结点或后继节点会是（1）（2）（3）中的其中一种】

总结：对非叶子结点的删除最后都会转化成对叶子节点的删除。

AVL树的查找效率很高，但是由于插入、删除时需要通过旋转来维持平衡度，所以创建一个AVL树的成本其实不小，由此诞生了平衡度不那么严格的红黑树。

红黑树（Red Black Tree，RBT)

Java 中的 TreeMap，JDK 1.8 中的 HashMap、C++ STL 中的 map 均是基于红黑树结构实现的

内容引自：

什么是红黑树，一篇文章解决所有疑惑~~ - 知乎 (zhihu.com)

特点

红黑树（Red Black Tree）是一颗自平衡（self-balancing）的二叉排序树（BST），树上的每一个结点都遵循下面的规则（特别提醒，这里的自平衡和平衡二叉树AVL的高度平衡有别）：

每一个结点都有一个颜色，要么为红色，要么为黑色；
树的根结点、叶子节点（外部节点，空节点）都是**黑色，**这里的叶子节点指的是最底层的空节点（外部节点），下图中的那些null节点才是叶子节点，null节点的父节点在红黑树里不将其看作叶子节点
树中不存在两个相邻的红色结点（即红色结点的父结点和孩子结点均不能是红色）；
从任意一个结点 （包括根结点）到其任何后代 NULL 结点（默认是黑色的）的每条路径都具有相同数量的黑色结点。

黑高（Black Height)

在一颗红黑树中，从某个结点 x 出发（不包含该结点）到达一个叶结点的任意一条简单路径上包含的黑色结点的数目称为黑高，记为 bh(x) 。

红黑树的黑高则为其根结点的黑高 。根据红黑树的性质 3、4，一颗红黑树的黑高bh >= h/2

引理：一棵有n个内部结点的红黑树的高度 h <= 2lg(n+1)。

现有如下图所示的一颗红黑树，将其中红色结点合入其黑色父结点可得到下右图

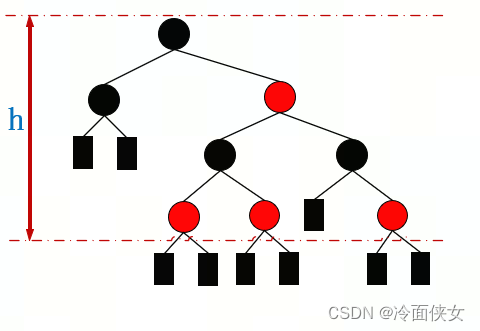
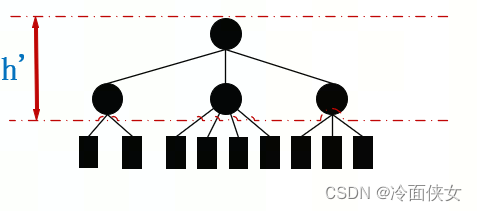
合并后的红黑树变成了一个2-3-4树，每个结点拥有2、3或4个子结点，假设该树有n+1个叶子结点，则有；

对于具有N个结点的红黑树而言则有即，根据可以得到，所以红黑树的插入、删除、查找的时间复杂度都是O(logn).

当涉及到频繁的插入和删除操作，优先选择红黑树；当涉及的插入和删除不频繁，而查找操作相对来说更频繁时，优先选择AVL树。

B树（平衡多路查找树，B-树）

内容引自：

B树和B+树_b+树顺序写-CSDN博客

B树和AVL树的区别是B树属于多叉树，一个结点的查找路径不止左右两个，而是多个。数据库索引技术里大量使用B树和B+树。

B树的阶数：M阶表示一个B树的结最多有M个查找路径。M=2是二叉树。

特点（以M阶B树为例）

1、每个结点的值（索引）按递增次序排列；

2、根结点的子结点个数为[2, M]；

3、除根结点外的非叶子结点的子结点个数为[Math.ceil(M/2), M]，Math.ceil()为向上取整；

4、每个非叶子结点的值（索引）个数=子结点个数-1。最小为Math.ceil(M/2)-1，最大为M-1；

5、B树的所有叶子结点位于同一层。

如下图一个3阶B树：

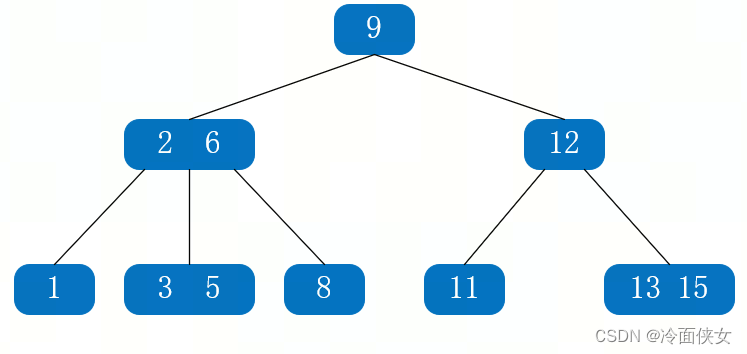
可以看出：

除根结点外，所有非叶子结点都至少有M/2=1.5取整=2个结点；
每个结点中的索引值都是从小到大排序的；
所有的叶子结点都在同一层；

查找

以查找结点5为例：

（1）第一次读IO，把结点9读入内存，再与目标数5比较，5小于9，往9的左边走；

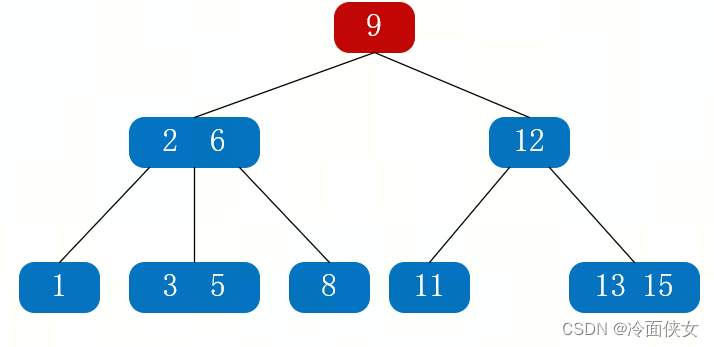
（2）第二次读IO，把结点2、6读入内存，然后比较结点中的2和6与目标值5，5大于2小于6，所以往中间路径走；

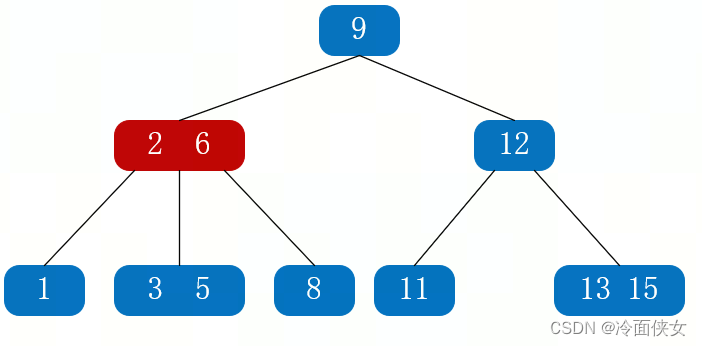
（3）第三次读IO，把结点3、5读入内存，然后发现结点中有5，因此找到目标值。

1、在数据库查询中，以树存储数据，树有多少层，就意味着要读取多少次磁盘IO，而读取IO是很费时间的操作。当数据量非常大时，用AVL树存的话，树高肯定很高，那么读取IO的次数也会很多，而B树的出现就是为了压缩树的高度。B树的一个结点装多个值，对结点的处理在内存中，速度就快了很多；

2、B树的每一个结点都包含key（索引值）和value（对应数据），因此离根结点越近的元素查找起来会更快（相比于B+树）。

插入（结点分裂）

以5阶B树为例，在空树中插入39：

继续插入22,41,97：

此时，再插入一个53，超过了允许的最大索引个数4，以中心元素41分裂：

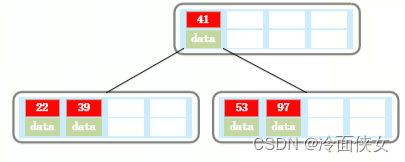
继续插入13,21：

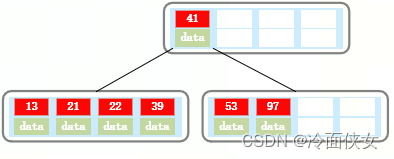
此时再插入一个40，其中一个结点中有13,21,22,39,40五个元素，超过了4，以中心元素22进行分裂，分裂出的22进位到上一层的结点中：

继续插入30,27：

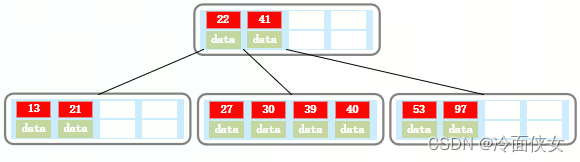
此时再插入一个33，其中一个结点中会有27,30,33,39,40五个元素，超过了4，以中心元素33进行分裂，分裂出的33进位到上一层结点中：

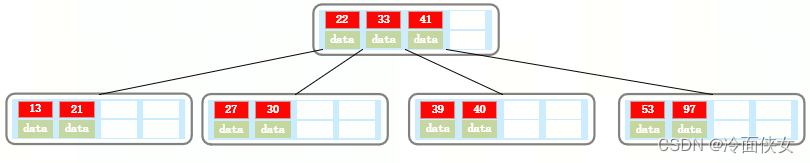
继续插入36,35：

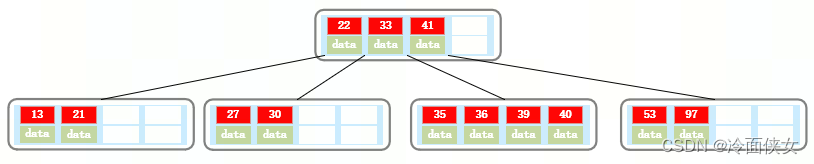
此时插入一个34，会有一个结点中有34,35,36,39,40五个元素，以中心元素36进行分裂，分裂出的36进位到上一层结点中：

继续插入24,29：

此时插入一个26，其中一个结点中有24,26,27,29,30五个元素，以中心元素27进行分裂，分裂出的27进位到上一层结点中时，会导致上一层结点拥有22,27,33,36,41五个元素，继续以中心元素33进行分裂：

删除

原始状态：

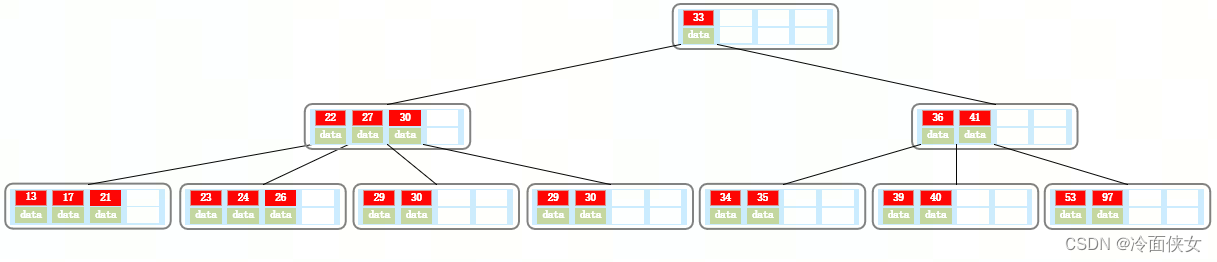
删除21：

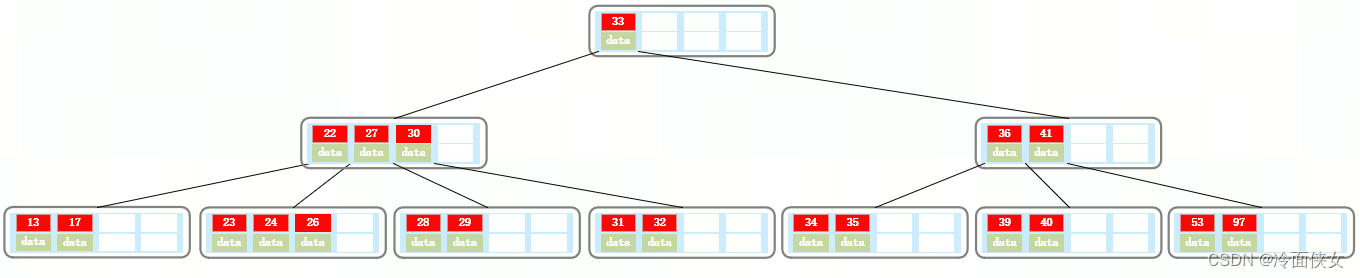
删除后的结点索引数仍然大于等于2（Math.ceil(5/2)-1=2），因此删除结束。

继续删除27，27是非叶子结点，所以删除27的话，要用27的后继28替代它，删除原来的28，

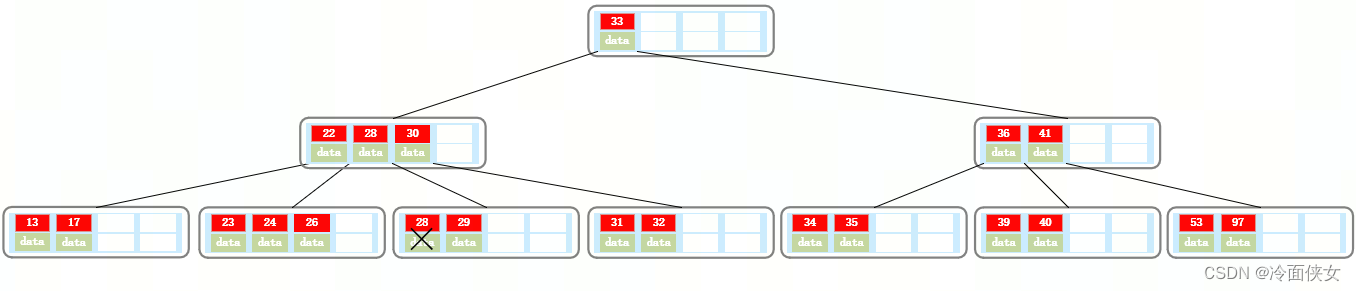
但是28删除后，它所在的结点索引个数只剩下1个，（此时可以向这个结点的右兄弟借一个索引值31，但不是直接拿，而是将父结点的索引30下移到本结点，然后将31上移到父结点，但这个时候右兄弟的索引个数又只剩下1个，需要父结点下沉31，并和本结点合并为一个结点：

）

另一种情况，此时可以向这个结点的左兄弟借一个索引值26，将父结点的索引28下移到本结点，然后将26上移到父结点：

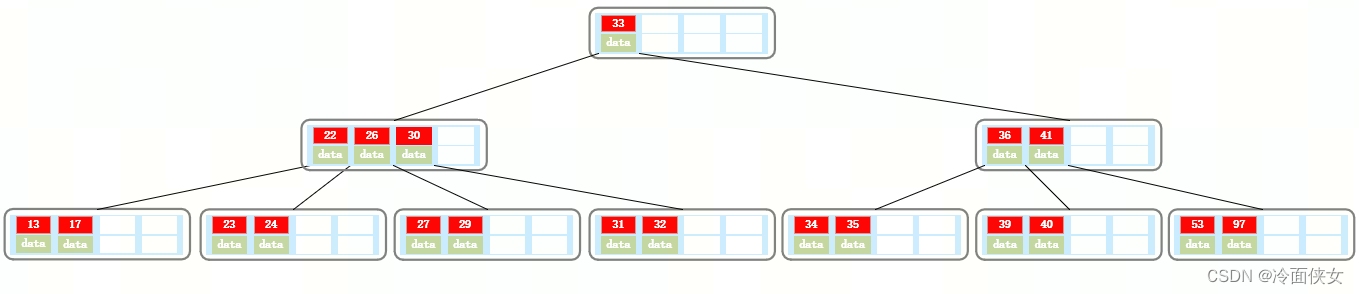
继续删除32,删除32后结点只剩下一个索引值，并且左右兄弟结点都只有2个索引值，不能借，只能让父结点下移索引值30，并跟左兄弟合并成一个结点：

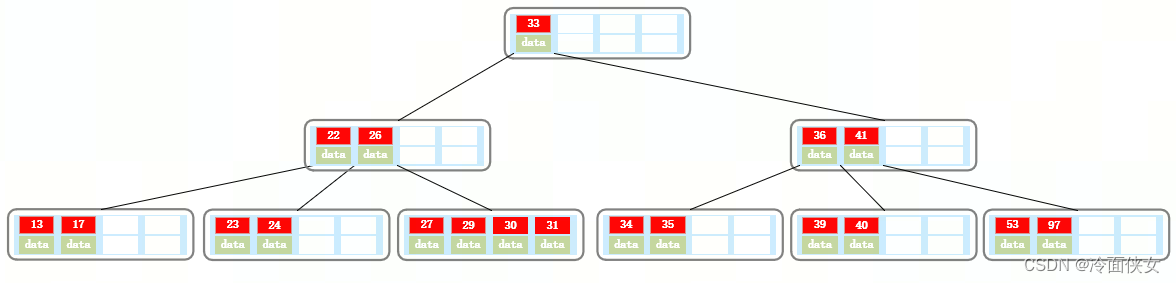
继续删除40，删除40后结点只剩下一个索引值，并且左右兄弟都只有2个索引值，只能让父结点下移索引值36，并跟左兄弟合并成一个结点，但是此时父结点只有一个索引值41，它的左兄弟也只有2个索引值，还需要它的父结点下移索引值，并跟它的左兄弟合并成一个结点：

B+树

B+树基于B树被提出，下图是一颗4阶B+树：

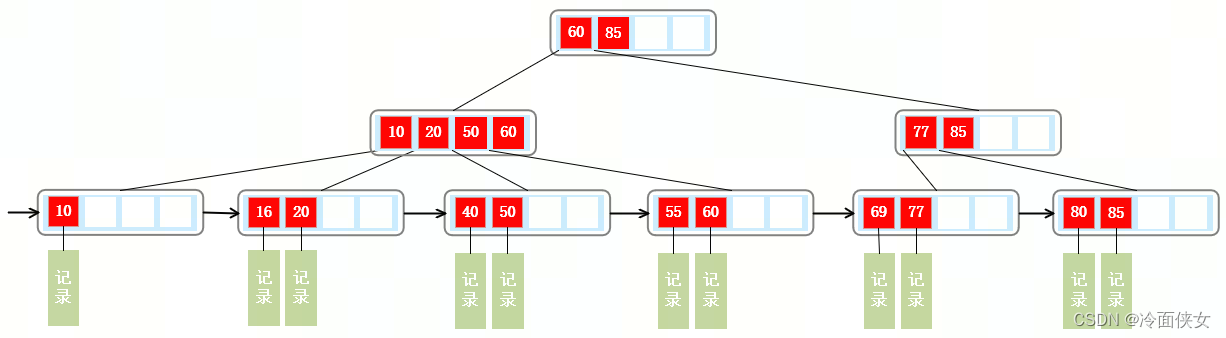
B树和B+树的区别：

B+内有两种结点，一种是索引结点，一种是叶子结点；
B+树的索引结点不会保存记录，只用于索引，所有数据保存在B+树的叶子结点中，而B树所有结点都会保存数据；
B+树的叶子结点都会被连成一条链表，叶子本身按索引值从小到大排序，方便范围查找数据；
B树的所有索引值不会重复，B+树非叶子结点的索引值最后一定会出现在叶子结点中。

为什么有B+树？

解释这个问题要从B树的优点和缺点说起：

B树的优点：

B树的每个结点都有key（索引值）和value（对应数据），因此方位离根结点近的元素查找起来会更快速（相对于B+树）；

B树的缺点：

不利于范围查找（区间查找），如果要找0~100的索引值，B树需要多次从根结点逐个查找，而B+树由于叶子结点都有链表，且链表中按照索引值从小到大排列，可以直接通过遍历链表实现范围查找。

哈夫曼树

数据结构------哈夫曼树（Huffman Tree） - 知乎 (zhihu.com)

特点

给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

基本术语

路径：在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路
路径长度：通路中分支的数目，若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1

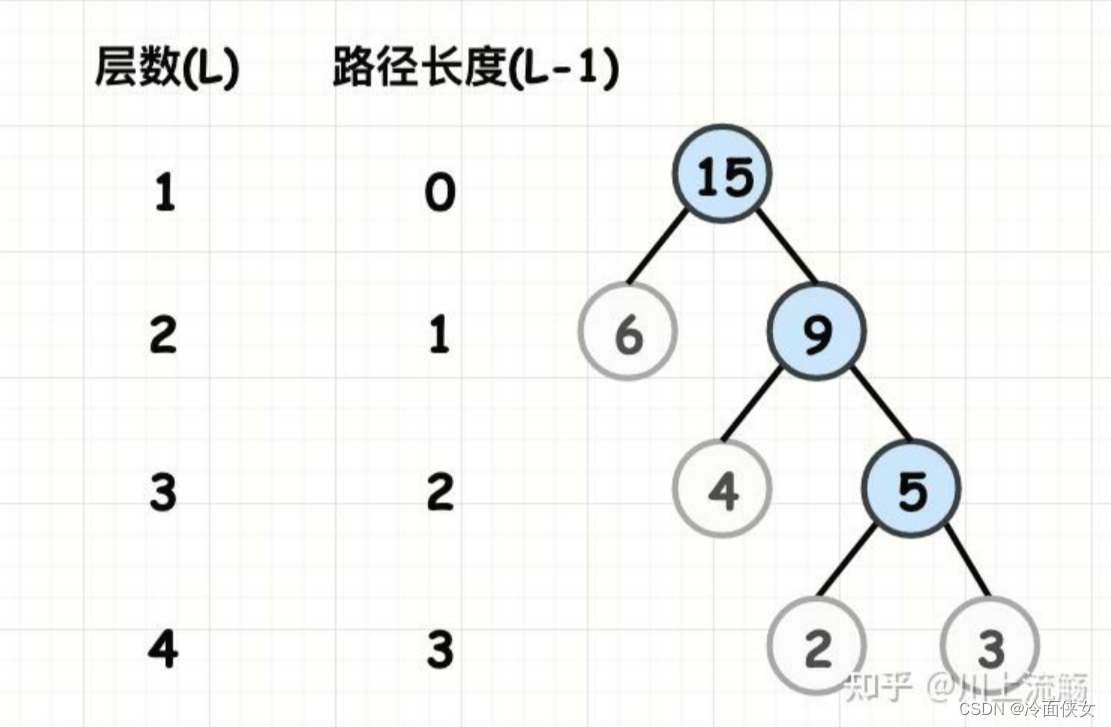
结点的权：将树中结点赋给一个有着某种含义的数值
结点的带权路径长度：从根结点到该结点之间的路径长度与该结点的权的乘积

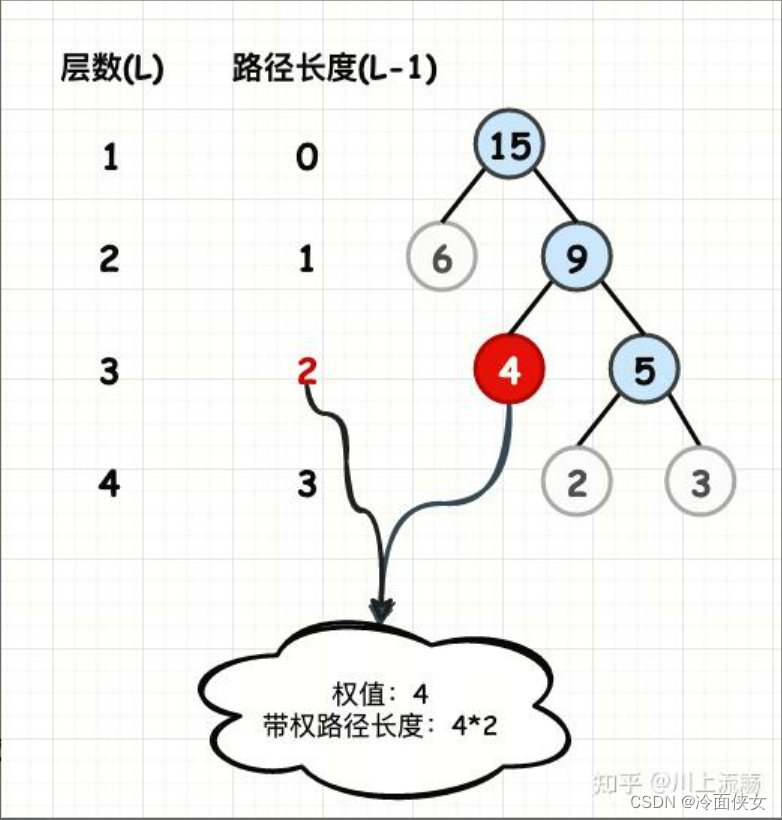
树的带权路径长度：所有叶子结点的带权路径长度之和，记为WPL。如上图：数的带权路径长度为：WPL = (2+3) * 3 + 4 * 2 + 6 * 1 = 29

构造

假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、...、wn，则哈夫曼树的构造规则为：

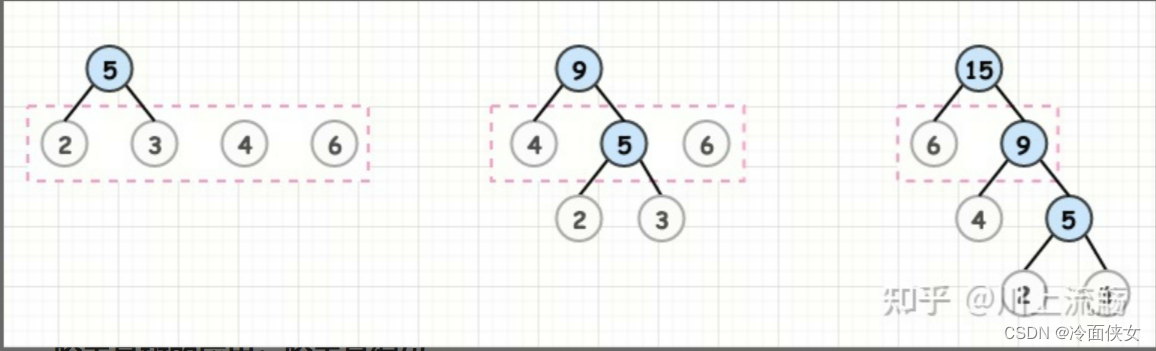
(1) 将w1、w2、...，wn看成是有n 棵树的森林(每棵树仅有一个结点)；

(2) 在森林中选出两个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；

(3)从森林中删除选取的两棵树，并将新树加入森林；

(4)重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。

例如：对 2，3，4，6 这四个数进行构造：