《算法导论》第 27 章 - 多线程算法

啊阿狸不会拉杆2025-08-18 15:28

引言

多线程算法是现代计算机科学中的重要组成部分，随着多核处理器的普及，如何充分利用硬件资源提高算法效率成为关键问题。《算法导论》第 27 章深入探讨了多线程算法的设计与分析，本文将对该章节内容进行详细解读，并提供可直接运行的 C++ 代码实现，帮助读者更好地理解和应用多线程算法。

思维导图

27.1 动态多线程基础

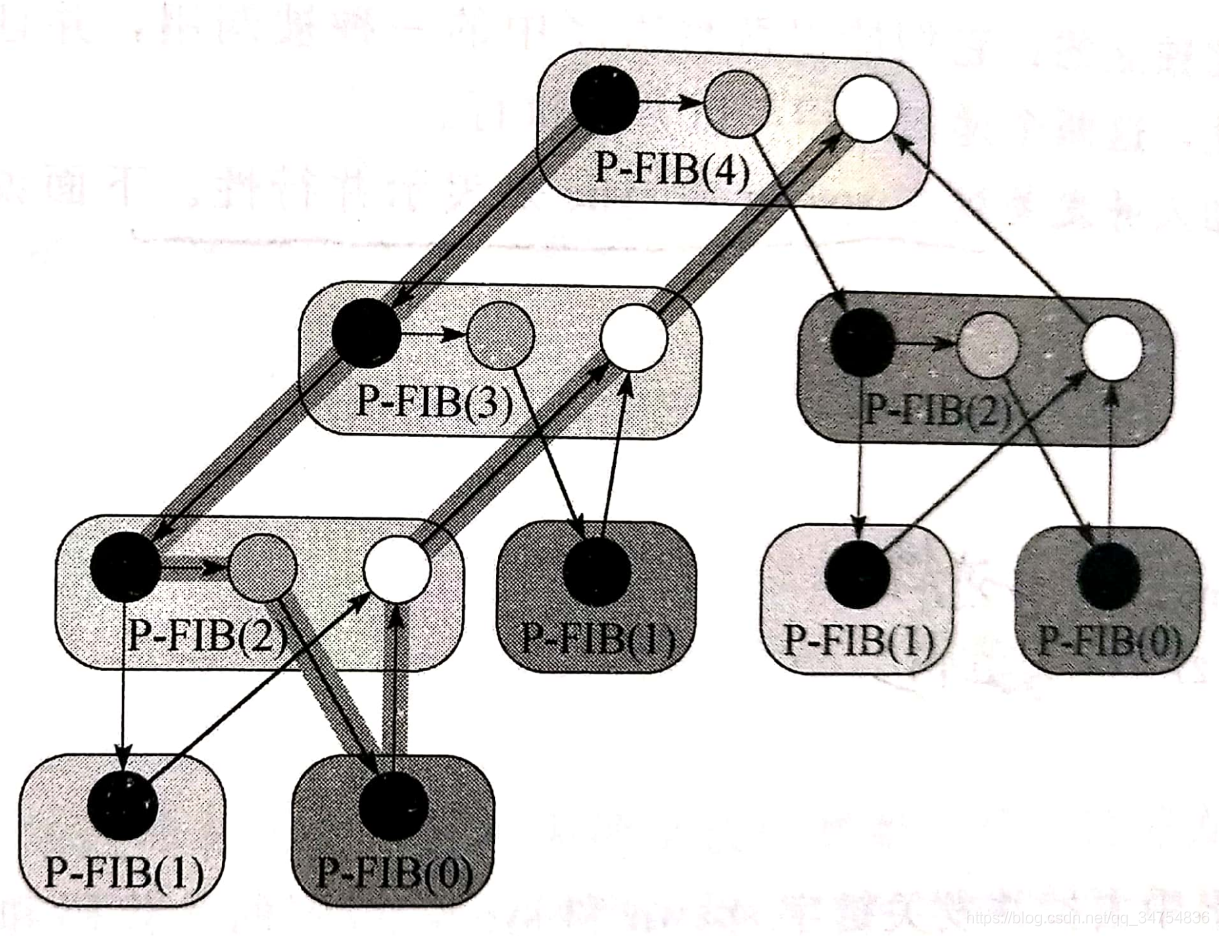
动态多线程是一种用于设计并行算法的模型，它允许程序在运行时动态地创建和调度线程，从而更灵活地利用多核处理器资源。

基本概念

  1. 工作量 (Work) : 算法在单处理器上执行所需的总步骤数，即所有线程执行的步骤总和。
  2. 持续时间 (Span) : 算法在拥有无限多处理器的情况下执行所需的最小步骤数，即关键路径的长度。
  3. 并行度 (Parallelism) : 工作量与持续时间的比值，反映了算法的并行潜力。

动态多线程模型

动态多线程模型使用两种基本操作来创建并行计算：

  1. parallel: 用于指定并行执行的代码块
  2. spawn : 用于创建新线程，允许父线程和子线程并行执行
  3. sync: 用于等待所有子线程完成

贪心调度

在实际应用中，处理器数量是有限的。贪心调度器能够保证：如果一个多线程算法的工作量为 T1，持续时间为 T∞，那么在 P 个处理器上的执行时间 Tp 满足：

Tp ≤ T1/P + T∞

这保证了只要并行度足够高，增加处理器就能有效减少执行时间。

示例代码：并行求和

下面是一个使用 C++11 及以上标准实现的并行求和算法，展示了动态多线程的基本应用：

cpp 复制代码 
#include <iostream>
#include <vector>
#include <thread>
#include <numeric>
#include <algorithm>
#include <chrono>  // 新增：用于计时

using namespace std;

// 并行求和函数
// 参数：v - 要求和的向量
//      start, end - 求和的范围
//      result - 存储结果的引用
//      threshold - 当子问题规模小于此值时，使用串行计算
void parallel_sum(const vector<int>& v, int start, int end, int& result, int threshold) {
    // 如果问题规模足够小，则使用串行计算
    if (end - start <= threshold) {
        result = accumulate(v.begin() + start, v.begin() + end, 0);
        return;
    }
    
    // 否则，将问题分成两半，并行计算
    int mid = start + (end - start) / 2;
    int left_sum, right_sum;
    
    // 创建线程计算左半部分，使用std::thread
    std::thread left_thread(parallel_sum, std::cref(v), start, mid, std::ref(left_sum), threshold);
    
    // 主线程计算右半部分
    parallel_sum(v, mid, end, right_sum, threshold);
    
    // 等待左半部分计算完成
    left_thread.join();
    
    // 合并结果
    result = left_sum + right_sum;
}

// 封装函数，方便调用
int parallel_sum(const vector<int>& v, int threshold = 1000) {
    if (v.empty()) return 0;
    int result;
    parallel_sum(v, 0, v.size(), result, threshold);
    return result;
}

int main() {
    // 创建一个包含100万个随机数的向量
    const int size = 1000000;
    vector<int> v(size);
    for (int i = 0; i < size; ++i) {
        v[i] = rand() % 100;
    }
    
    // 串行求和
    auto start = chrono::high_resolution_clock::now();
    int serial_result = accumulate(v.begin(), v.end(), 0);
    auto serial_end = chrono::high_resolution_clock::now();
    chrono::duration<double> serial_time = serial_end - start;
    
    // 并行求和
    start = chrono::high_resolution_clock::now();
    int parallel_result = parallel_sum(v);
    auto parallel_end = chrono::high_resolution_clock::now();
    chrono::duration<double> parallel_time = parallel_end - start;
    
    // 输出结果
    cout << "串行求和结果: " << serial_result << endl;
    cout << "并行求和结果: " << parallel_result << endl;
    cout << "串行时间: " << serial_time.count() << " 秒" << endl;
    cout << "并行时间: " << parallel_time.count() << " 秒" << endl;
    cout << "加速比: " << serial_time.count() / parallel_time.count() << endl;
    
    return 0;
}

代码说明

上述代码实现了一个并行求和算法，其核心思想是：

  1. 当问题规模较大时，将数组分成两半
  2. 使用一个新线程计算左半部分的和
  3. 主线程同时计算右半部分的和
  4. 等待两个线程都完成后，将结果相加

算法中引入了阈值 (threshold) 参数，当子问题规模小于阈值时，使用串行计算，这是因为对于过小的问题，创建线程的开销可能超过并行计算带来的收益。

并行求和流程图

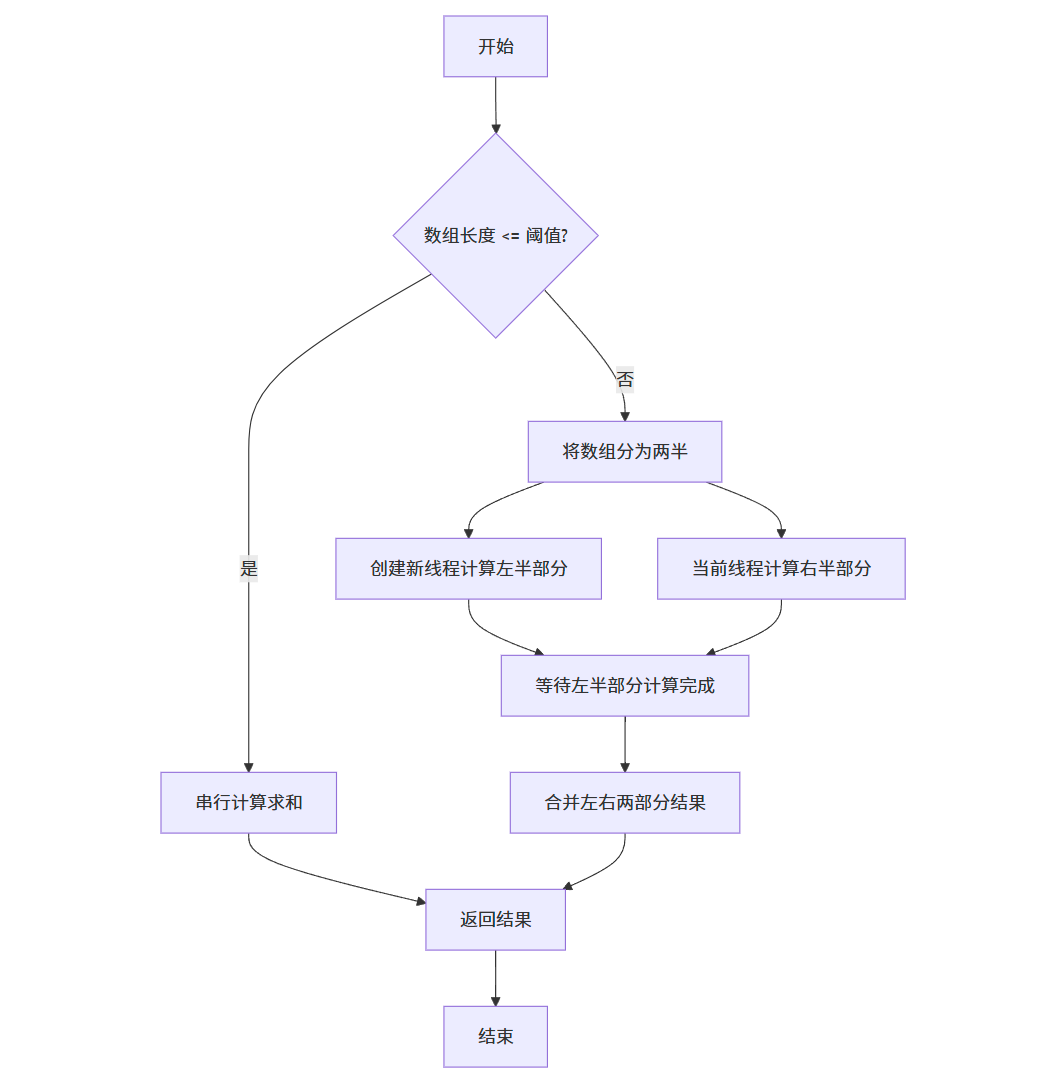
27.2 多线程矩阵乘法

矩阵乘法是科学计算中的基本操作，其计算密集型特性使其非常适合并行化。

矩阵乘法回顾

对于两个矩阵 A 和 B，其中 A 是 n×m 矩阵，B 是 m×p 矩阵，它们的乘积 C 是一个 n×p 矩阵，其中：

C[i][j] = Σ(k=1 to m) A[i][k] × B[k][j]

串行实现的时间复杂度为 O (nmp)。

多线程矩阵乘法思路

矩阵乘法的并行化可以从多个层次进行：

  1. 元素级并行：每个元素 C [i][j] 的计算可以独立进行
  2. 行级并行：每一行的元素可以并行计算
  3. 分块并行：将矩阵分成块，块之间可以并行计算

下面我们实现一个分块的多线程矩阵乘法，它在性能和可扩展性之间取得了很好的平衡。

示例代码：多线程矩阵乘法

cpp 复制代码 
#include <iostream>
#include <vector>
#include <thread>
#include <chrono>
#include <cstdlib>
#include <algorithm>

using namespace std;

// 定义矩阵类型
using Matrix = vector<vector<int>>;

// 生成随机矩阵
Matrix generate_random_matrix(int rows, int cols, int min_val = 0, int max_val = 10) {
    Matrix mat(rows, vector<int>(cols));
    for (int i = 0; i < rows; ++i) {
        for (int j = 0; j < cols; ++j) {
            mat[i][j] = min_val + rand() % (max_val - min_val + 1);
        }
    }
    return mat;
}

// 串行矩阵乘法
Matrix serial_matrix_multiply(const Matrix& A, const Matrix& B) {
    int n = A.size();
    int m = B.size();
    int p = B[0].size();
    
    Matrix C(n, vector<int>(p, 0));
    
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < p; ++j) {
            for (int k = 0; k < m; ++k) {
                C[i][j] += A[i][k] * B[k][j];
            }
        }
    }
    
    return C;
}

// 计算矩阵块的乘积
void multiply_block(const Matrix& A, const Matrix& B, Matrix& C, 
                   int a_start, int a_end, 
                   int b_start, int b_end, 
                   int c_row, int c_col) {
    int block_size = a_end - a_start;
    
    for (int i = 0; i < block_size; ++i) {
        for (int j = 0; j < block_size; ++j) {
            for (int k = 0; k < block_size; ++k) {
                C[c_row + i][c_col + j] += A[a_start + i][b_start + k] * B[b_start + k][b_end + j];
            }
        }
    }
}

// 多线程矩阵乘法（分块实现）
Matrix parallel_matrix_multiply(const Matrix& A, const Matrix& B, int block_size = 64) {
    int n = A.size();
    int m = B.size();
    int p = B[0].size();
    
    // 确保矩阵可以被块大小整除（实际应用中可能需要处理边界情况）
    if (n % block_size != 0 || m % block_size != 0 || p % block_size != 0) {
        cerr << "矩阵大小必须是块大小的整数倍" << endl;
        return Matrix();
    }
    
    Matrix C(n, vector<int>(p, 0));
    vector<thread> threads;
    
    // 分块并行计算
    for (int i = 0; i < n; i += block_size) {
        for (int j = 0; j < p; j += block_size) {
            for (int k = 0; k < m; k += block_size) {
                // 创建线程计算块乘积
                threads.emplace_back(multiply_block, cref(A), cref(B), ref(C),
                                    i, i + block_size,
                                    k, k + block_size,
                                    i, j);
            }
        }
    }
    
    // 等待所有线程完成
    for (auto& t : threads) {
        t.join();
    }
    
    return C;
}

// 验证两个矩阵是否相等
bool matrices_equal(const Matrix& A, const Matrix& B) {
    if (A.size() != B.size()) return false;
    if (A.empty()) return true;
    if (A[0].size() != B[0].size()) return false;
    
    for (int i = 0; i < A.size(); ++i) {
        for (int j = 0; j < A[0].size(); ++j) {
            if (A[i][j] != B[i][j]) return false;
        }
    }
    return true;
}

// 打印矩阵（用于调试）
void print_matrix(const Matrix& mat, int max_rows = 5, int max_cols = 5) {
    int rows = min((int)mat.size(), max_rows);
    if (rows == 0) {
        cout << "空矩阵" << endl;
        return;
    }
    int cols = min((int)mat[0].size(), max_cols);
    
    for (int i = 0; i < rows; ++i) {
        for (int j = 0; j < cols; ++j) {
            cout << mat[i][j] << "\t";
        }
        if (cols < mat[0].size()) cout << "...";
        cout << endl;
    }
    if (rows < mat.size()) cout << "..." << endl;
}

int main() {
    srand(time(0));
    
    // 矩阵大小 (可根据需要调整)
    const int n = 512;
    const int m = 512;
    const int p = 512;
    
    // 生成随机矩阵
    cout << "生成随机矩阵 A(" << n << "x" << m << ") 和 B(" << m << "x" << p << ")..." << endl;
    Matrix A = generate_random_matrix(n, m);
    Matrix B = generate_random_matrix(m, p);
    
    // 串行矩阵乘法
    cout << "执行串行矩阵乘法..." << endl;
    auto start = chrono::high_resolution_clock::now();
    Matrix C_serial = serial_matrix_multiply(A, B);
    auto serial_end = chrono::high_resolution_clock::now();
    chrono::duration<double> serial_time = serial_end - start;
    
    // 并行矩阵乘法
    cout << "执行并行矩阵乘法..." << endl;
    start = chrono::high_resolution_clock::now();
    Matrix C_parallel = parallel_matrix_multiply(A, B);
    auto parallel_end = chrono::high_resolution_clock::now();
    chrono::duration<double> parallel_time = parallel_end - start;
    
    // 验证结果
    bool results_match = matrices_equal(C_serial, C_parallel);
    cout << "结果验证: " << (results_match ? "成功 (串行和并行结果一致)" : "失败 (结果不一致)") << endl;
    
    // 输出部分结果
    cout << endl << "矩阵 A 的前5x5部分:" << endl;
    print_matrix(A);
    cout << endl << "矩阵 B 的前5x5部分:" << endl;
    print_matrix(B);
    cout << endl << "乘积矩阵 C 的前5x5部分:" << endl;
    print_matrix(C_serial);
    
    // 输出性能数据
    cout << endl << "性能数据:" << endl;
    cout << "串行计算时间: " << serial_time.count() << " 秒" << endl;
    cout << "并行计算时间: " << parallel_time.count() << " 秒" << endl;
    cout << "加速比: " << serial_time.count() / parallel_time.count() << endl;
    
    return 0;
}

代码说明

上述代码实现了一个分块的多线程矩阵乘法，主要特点包括：

  1. 将大矩阵分成固定大小的块，每个块的乘法可以并行进行
  2. 使用 C++11 的 thread 库创建线程，每个线程负责计算一个块的乘积
  3. 实现了结果验证功能，确保并行计算结果与串行计算结果一致
  4. 包含了性能测试代码，可以比较串行和并行版本的执行时间

分块大小 (block_size) 是一个重要的参数，通常应根据硬件缓存大小进行调整，以提高缓存利用率。其中 bs 表示块大小 (block_size)。

27.3 多线程归并排序

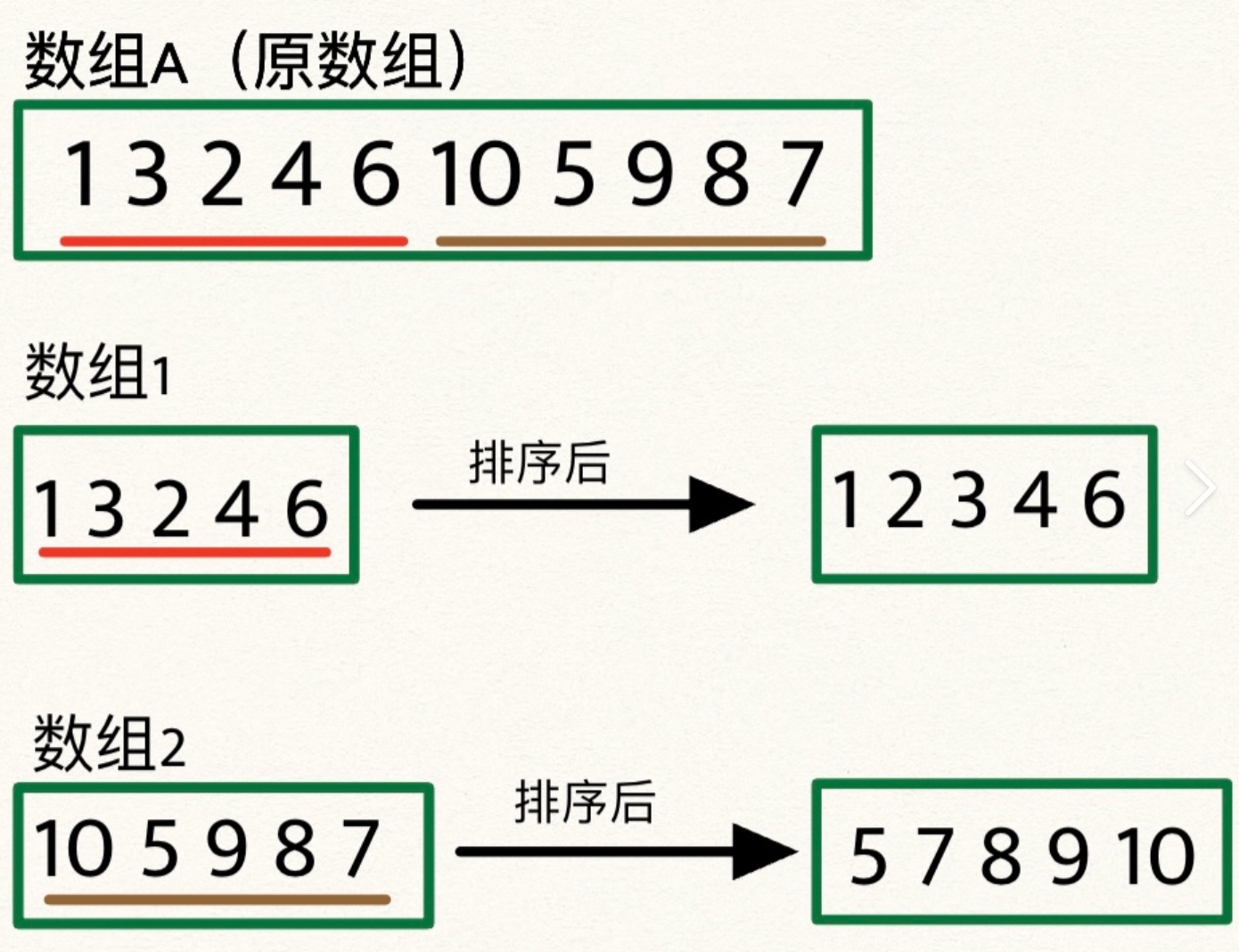
归并排序是一种分治算法，其自然的递归结构使其非常适合并行化。

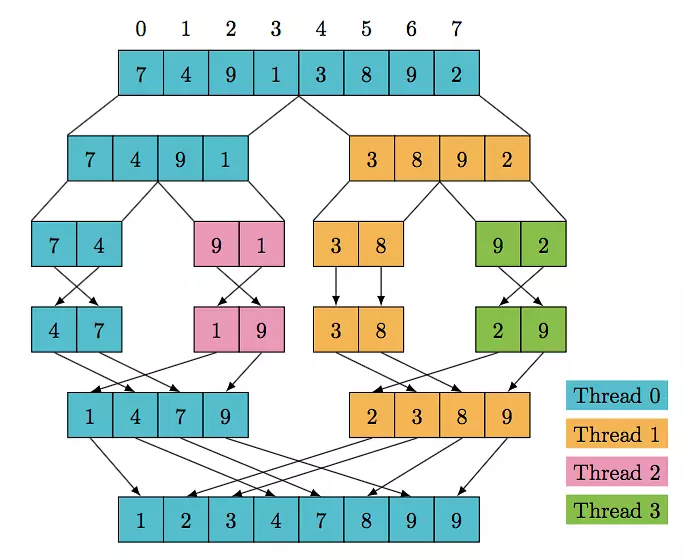
归并排序回顾

归并排序的基本步骤：

  1. 将数组分成两个 halves
  2. 递归地对每个 half 进行排序
  3. 合并两个已排序的 halves

串行归并排序的时间复杂度为 O (n log n)。

多线程归并排序思路

多线程归并排序可以在分治的各个阶段进行并行化：

  1. 在分割阶段，可以并行地对左右两个子数组进行排序
  2. 在合并阶段，可以使用多线程进行合并操作

下面实现一个多线程归并排序算法，在分割阶段进行并行化。

示例代码：多线程归并排序

cpp 复制代码 
#include <iostream>
#include <vector>
#include <thread>
#include <chrono>
#include <algorithm>
#include <random>

using namespace std;

// 合并两个已排序的子数组
// 参数：arr - 原始数组
//      left, mid, right - 数组索引，[left, mid]和[mid+1, right]是两个已排序的子数组
//      temp - 临时数组，用于存储合并结果
void merge(vector<int>& arr, int left, int mid, int right, vector<int>& temp) {
    int i = left;     // 左子数组的起始索引
    int j = mid + 1;  // 右子数组的起始索引
    int k = left;     // 临时数组的起始索引
    
    // 合并两个子数组
    while (i <= mid && j <= right) {
        if (arr[i] <= arr[j]) {
            temp[k++] = arr[i++];
        } else {
            temp[k++] = arr[j++];
        }
    }
    
    // 复制左子数组的剩余元素
    while (i <= mid) {
        temp[k++] = arr[i++];
    }
    
    // 复制右子数组的剩余元素
    while (j <= right) {
        temp[k++] = arr[j++];
    }
    
    // 将合并结果复制回原始数组
    for (i = left; i <= right; ++i) {
        arr[i] = temp[i];
    }
}

// 串行归并排序
void serial_merge_sort(vector<int>& arr, int left, int right, vector<int>& temp) {
    if (left < right) {
        int mid = left + (right - left) / 2;
        
        // 递归排序左半部分
        serial_merge_sort(arr, left, mid, temp);
        // 递归排序右半部分
        serial_merge_sort(arr, mid + 1, right, temp);
        // 合并两个已排序的部分
        merge(arr, left, mid, right, temp);
    }
}

// 多线程归并排序
void parallel_merge_sort(vector<int>& arr, int left, int right, vector<int>& temp, int threshold = 1000) {
    if (left < right) {
        // 如果子数组大小小于阈值，则使用串行排序
        if (right - left + 1 <= threshold) {
            serial_merge_sort(arr, left, right, temp);
            return;
        }
        
        int mid = left + (right - left) / 2;
        
        // 创建线程排序左半部分
        thread left_thread(parallel_merge_sort, ref(arr), left, mid, ref(temp), threshold);
        
        // 当前线程排序右半部分
        parallel_merge_sort(arr, mid + 1, right, temp, threshold);
        
        // 等待左半部分排序完成
        left_thread.join();
        
        // 合并两个已排序的部分
        merge(arr, left, mid, right, temp);
    }
}

// 封装函数，方便调用
void parallel_merge_sort(vector<int>& arr, int threshold = 1000) {
    if (arr.size() <= 1) return;
    vector<int> temp(arr.size());
    parallel_merge_sort(arr, 0, arr.size() - 1, temp, threshold);
}

// 生成随机数组
vector<int> generate_random_array(int size, int min_val = 0, int max_val = 100000) {
    vector<int> arr(size);
    random_device rd;
    mt19937 gen(rd());
    uniform_int_distribution<> dis(min_val, max_val);
    
    for (int i = 0; i < size; ++i) {
        arr[i] = dis(gen);
    }
    
    return arr;
}

// 验证数组是否已排序
bool is_sorted(const vector<int>& arr) {
    for (int i = 1; i < arr.size(); ++i) {
        if (arr[i] < arr[i - 1]) {
            return false;
        }
    }
    return true;
}

// 打印数组的前n个和后n个元素
void print_array(const vector<int>& arr, int n = 10) {
    int size = arr.size();
    if (size <= 2 * n) {
        for (int num : arr) {
            cout << num << " ";
        }
    } else {
        for (int i = 0; i < n; ++i) {
            cout << arr[i] << " ";
        }
        cout << "... ";
        for (int i = size - n; i < size; ++i) {
            cout << arr[i] << " ";
        }
    }
    cout << endl;
}

int main() {
    // 数组大小 (可根据需要调整)
    const int size = 1000000;
    
    // 生成随机数组
    cout << "生成随机数组 (" << size << " 个元素)..." << endl;
    vector<int> arr_serial = generate_random_array(size);
    vector<int> arr_parallel = arr_serial;  // 复制数组用于并行排序
    
    // 串行归并排序
    cout << "执行串行归并排序..." << endl;
    auto start = chrono::high_resolution_clock::now();
    vector<int> temp_serial(size);
    serial_merge_sort(arr_serial, 0, size - 1, temp_serial);
    auto serial_end = chrono::high_resolution_clock::now();
    chrono::duration<double> serial_time = serial_end - start;
    
    // 并行归并排序
    cout << "执行并行归并排序..." << endl;
    start = chrono::high_resolution_clock::now();
    parallel_merge_sort(arr_parallel);
    auto parallel_end = chrono::high_resolution_clock::now();
    chrono::duration<double> parallel_time = parallel_end - start;
    
    // 验证排序结果
    bool serial_sorted = is_sorted(arr_serial);
    bool parallel_sorted = is_sorted(arr_parallel);
    bool results_equal = (arr_serial == arr_parallel);
    
    cout << "排序验证: " << endl;
    cout << "  串行排序结果: " << (serial_sorted ? "正确" : "错误") << endl;
    cout << "  并行排序结果: " << (parallel_sorted ? "正确" : "错误") << endl;
    cout << "  结果一致性: " << (results_equal ? "一致" : "不一致") << endl;
    
    // 输出部分排序结果
    cout << endl << "排序结果 (前10个和后10个元素):" << endl;
    print_array(arr_serial);
    
    // 输出性能数据
    cout << endl << "性能数据:" << endl;
    cout << "串行排序时间: " << serial_time.count() << " 秒" << endl;
    cout << "并行排序时间: " << parallel_time.count() << " 秒" << endl;
    cout << "加速比: " << serial_time.count() / parallel_time.count() << endl;
    
    return 0;
}

代码说明

上述代码实现了一个多线程归并排序算法，其核心思想是：

  1. 当子数组大小大于阈值时，创建新线程对左半部分进行排序
  2. 当前线程同时对右半部分进行排序
  3. 等待两个线程完成后，合并两个已排序的子数组
  4. 当子数组大小小于阈值时，使用串行排序，避免创建过多线程带来的开销

算法中引入了阈值 (threshold) 参数，这是一个重要的调优参数，它决定了何时使用并行排序，何时使用串行排序。

思考题

  1. 并行度分析：分析多线程矩阵乘法和多线程归并排序的工作量、持续时间和并行度。在什么情况下，增加处理器数量可以显著提高性能？

  2. 阈值优化：在本文实现的多线程算法中，都使用了阈值来决定何时使用并行计算，何时使用串行计算。请设计一个实验，确定不同硬件环境下的最佳阈值。

  3. 负载均衡：在多线程矩阵乘法中，所有线程的工作量基本相同，实现了较好的负载均衡。请思考：在哪些情况下，多线程算法可能会出现负载不均衡的问题？如何解决？

  4. 并行合并：本文实现的多线程归并排序仅在分割阶段进行了并行化，合并阶段仍然是串行的。请设计一个并行合并算法，进一步提高归并排序的并行度。

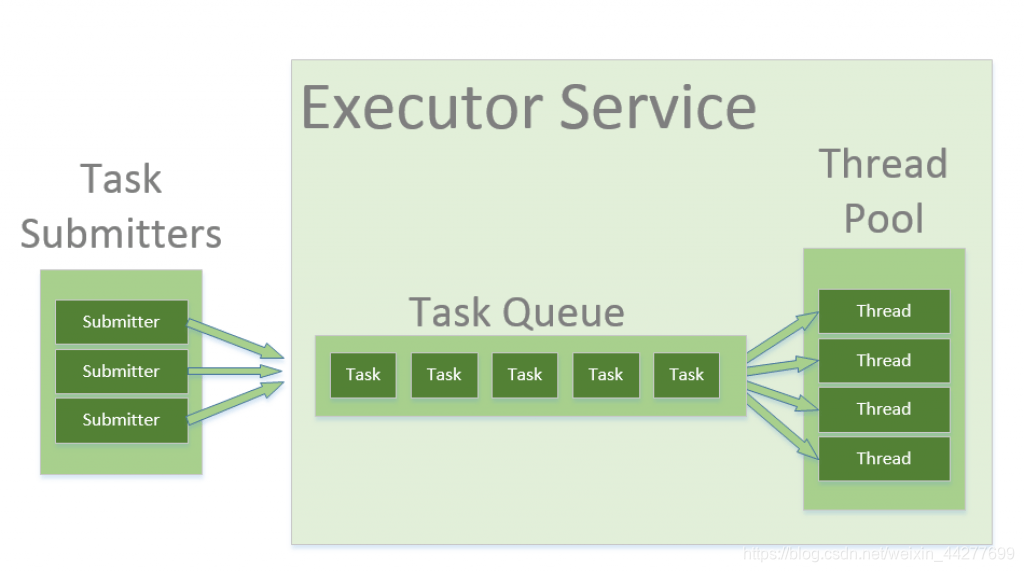
  5. 线程池：本文直接使用了 C++ 的 thread 库创建线程，频繁创建和销毁线程会带来一定的开销。请使用线程池改进本文的多线程算法，减少线程管理开销。

本章注记

多线程算法是充分利用现代多核处理器的关键技术，它通过将计算任务分解为可以并行执行的子任务，显著提高了算法的执行效率。

本章介绍的动态多线程模型为设计并行算法提供了一个抽象框架，它屏蔽了底层线程调度的细节，使开发者可以专注于算法的并行结构设计。工作量、持续时间和并行度是评估多线程算法性能的重要指标，它们帮助我们理解算法的并行潜力和在不同处理器数量下的性能表现。

矩阵乘法和归并排序是多线程算法的典型应用案例，它们展示了如何将串行算法改造为高效的并行算法。这些案例中的分治策略具有普遍意义，可以应用于许多其他算法的并行化。

在实际应用中，多线程算法的性能还受到许多因素的影响，包括缓存利用率、内存带宽、线程同步开销等。因此，设计高效的多线程算法不仅需要考虑算法的理论复杂度，还需要结合具体的硬件环境进行优化。

随着处理器核心数量的不断增加，多线程算法将变得越来越重要。掌握多线程算法的设计思想和分析方法，对于开发高性能计算程序具有重要意义。

结语

本文详细介绍了《算法导论》第 27 章的多线程算法内容，包括动态多线程基础、多线程矩阵乘法和多线程归并排序，并提供了完整的 C++ 实现代码。希望通过本文的讲解和代码示例，读者能够深入理解多线程算法的设计思想和实现方法，并能够将这些知识应用到实际问题中。

多线程编程是一个复杂而广阔的领域，本文只是入门介绍。要真正掌握多线程算法，还需要不断实践和探索，结合具体应用场景进行优化和创新。

相关推荐
来旺1 天前
互联网大厂Java面试全解析及三轮问答专项
java·数据库·spring boot·安全·缓存·微服务·面试
Json____1 天前
使用node Express 框架框架开发一个前后端分离的二手交易平台项目。
java·前端·express
since �1 天前
前端转Java，从0到1学习教程
java·前端·学习
詩句☾⋆᭄南笙1 天前
Mybatis一对一、一对多
java·mybatis·resulttype·resultmap·一对多·一对一
深思慎考1 天前
RabbitMQ 入门：基于 AMQP-CPP 的 C++ 实践指南与二次封装
开发语言·c++·分布式·rabbitmq·api
深思慎考1 天前
Ubuntu 系统 RabbitMQ 安装指南与使用（含 C++ 客户端与 SSL 错误解决）
c++·ubuntu·rabbitmq·github·rabbitmqpp
Andya_net1 天前
Java | 基于redis实现分布式批量设置各个数据中心的服务器配置方案设计和代码实践
java·服务器·分布式
lang201509281 天前
Spring Boot 外部化配置最佳实践指南
java·spring boot
沐浴露z1 天前
【JVM】详解 垃圾回收
java·jvm·算法
重生之我要当java大帝1 天前
java微服务-尚医通-管理平台前端搭建-医院设置管理-4
java·开发语言·前端
热门推荐
01GitHub 镜像站点02BongoCat - 跨平台键盘猫动画工具03UV安装并设置国内源04GitLab 零基础入门指南：从安装到项目管理全流程05Linux下V2Ray安装配置指南06NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南07在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）082025软件测试面试八股文（含答案+文档）09两千字总结：Codex 国内如何安装和使用的教程，以及如何设置中文回答10KGG转MP3工具|非KGM文件|解密音频